Isomorphism in mathematics refers to a mapping between two structures that shows a one-to-one correspondence preserving their operations and relations. This concept is crucial for recognizing when two systems are fundamentally the same despite superficial differences. Explore the rest of the article to understand how isomorphism applies across different fields and its significance for your studies.
Table of Comparison
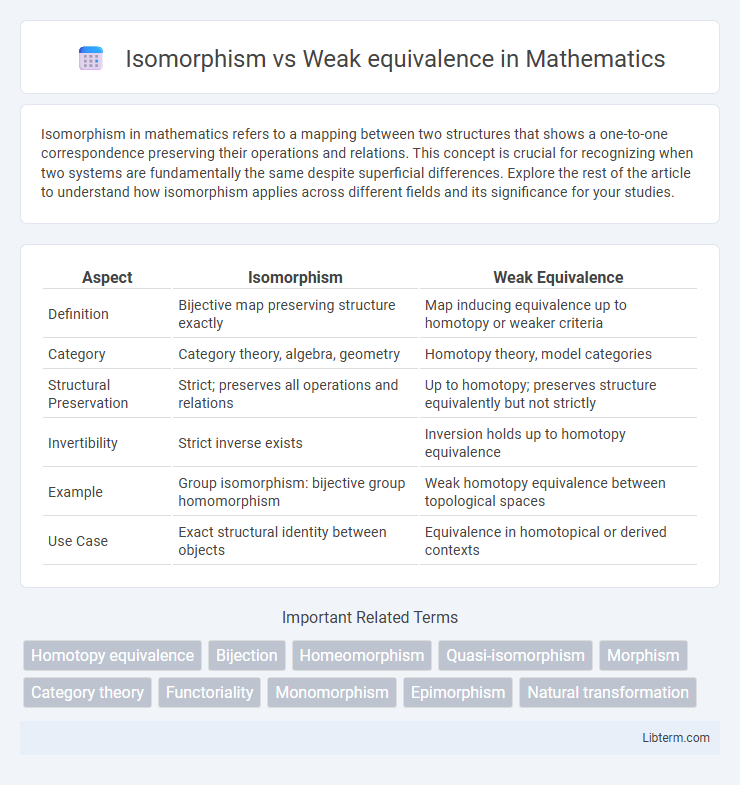
| Aspect | Isomorphism | Weak Equivalence |
|---|---|---|
| Definition | Bijective map preserving structure exactly | Map inducing equivalence up to homotopy or weaker criteria |
| Category | Category theory, algebra, geometry | Homotopy theory, model categories |
| Structural Preservation | Strict; preserves all operations and relations | Up to homotopy; preserves structure equivalently but not strictly |
| Invertibility | Strict inverse exists | Inversion holds up to homotopy equivalence |
| Example | Group isomorphism: bijective group homomorphism | Weak homotopy equivalence between topological spaces |
| Use Case | Exact structural identity between objects | Equivalence in homotopical or derived contexts |
Introduction to Isomorphism and Weak Equivalence
Isomorphism refers to a bijective mapping between two structures that preserves their properties and operations, ensuring they are structurally identical in a mathematical or categorical context. Weak equivalence relaxes these conditions by allowing mappings that preserve structure up to homotopy or other weaker criteria, often used in homotopy theory and abstract algebra. Understanding the distinction between strict isomorphisms and weak equivalences is crucial for analyzing when two objects can be considered essentially the same despite differences in finer structural details.
Defining Isomorphism in Mathematics
Isomorphism in mathematics defines a bijective mapping between two structures that preserves operations and relations, indicating they are structurally identical. Weak equivalence, by contrast, relaxes these constraints by allowing transformations that preserve properties up to homotopy or approximation rather than exact structure. Understanding isomorphism is crucial for classifying mathematical objects by their intrinsic properties rather than superficial differences.
What is Weak Equivalence?
Weak equivalence in mathematics, particularly in homotopy theory, refers to a morphism between topological spaces or objects that induces isomorphisms on all homotopy groups, thus preserving their essential 'shape' up to homotopy. Unlike isomorphism, which requires a bijective structure-preserving map, weak equivalence focuses on equivalence at the level of homotopy types rather than strict one-to-one correspondence. This concept plays a crucial role in model categories and abstract homotopy theory, enabling classification of spaces by their homotopy invariants rather than strict isomorphic structure.
Key Differences Between Isomorphism and Weak Equivalence
Isomorphism represents a strong form of equivalence where there exists a bijective structure-preserving map between two objects, ensuring they are identical in structure. Weak equivalence, often used in homotopy theory or category theory, allows for a more flexible comparison where objects are considered equivalent through maps inducing isomorphisms in specific invariants, such as homotopy groups, but may lack a strict bijection. The key difference lies in the rigidity of isomorphism, requiring exact structural matching, whereas weak equivalence accepts broader equivalences that preserve essential properties without demanding exact structural identity.
Mathematical Significance of Isomorphism
Isomorphism in mathematics denotes a bijective structure-preserving map between two objects, indicating they are fundamentally the same in form and properties, which allows for complete interchangeable analysis. Weak equivalence relaxes these conditions, preserving structure only up to homotopy or weaker criteria, thus recognizing objects as similar but not identical in a strict sense. The mathematical significance of isomorphism lies in its role as a definitive equivalence relation that guarantees identical algebraic or categorical structure, enabling exact transfer of results and properties.
The Role of Weak Equivalence in Category Theory
Weak equivalence in category theory generalizes the concept of isomorphism by allowing morphisms that induce equivalences up to homotopy or other weaker conditions rather than strict bijective correspondences. Unlike isomorphisms, which require exact inverses, weak equivalences identify objects that behave identically within a homotopical or model structure context, facilitating a flexible framework for comparing mathematical structures. This role is crucial in homotopy theory, where weak equivalences enable the construction of homotopy categories and serve as a foundation for understanding derived functors and localization.
Real-world Examples of Isomorphism
Isomorphism illustrates structural identity between two entities, such as chemical isomers that share the same molecular formula but differ in arrangement, preserving properties despite different appearances. In computer science, isomorphic graphs represent network structures identical in connectivity, enabling efficient data modeling and problem-solving. These real-world examples highlight how isomorphism ensures equivalence in underlying structure, contrasting with weak equivalence where similarity may exist without full structural preservation.
Applications of Weak Equivalence
Weak equivalence is crucial in homotopy theory, enabling comparisons between spaces that are "equivalent" up to homotopy, rather than strictly isomorphic, thus facilitating the study of topological spaces via homotopy categories. Applications of weak equivalence include simplifying complex structures in algebraic topology, such as in the classification of fiber bundles, model categories, and in the formulation of higher category theory concepts. This flexibility allows mathematicians to focus on essential topological properties without requiring exact structural matching, broadening the scope of analysis in modern mathematical frameworks.
Choosing Between Isomorphism and Weak Equivalence
Choosing between isomorphism and weak equivalence depends on the level of structural similarity required. Isomorphism demands a bijective, structure-preserving mapping that guarantees exact equivalence between objects in categories such as graph theory or algebra. Weak equivalence, typically used in homotopy theory or model categories, allows for more flexible identification of objects that have the same essential properties without requiring strict bijections, making it suitable when exact structural matching is unnecessary or too restrictive.
Conclusion: Isomorphism vs Weak Equivalence
Isomorphism denotes a strict structural sameness between mathematical objects, ensuring one-to-one correspondence and preserving all operations and relations exactly. Weak equivalence relaxes these conditions, allowing objects to be considered equivalent under less rigid transformations or up to homotopy, relevant in categories like homotopy theory and higher category theory. Understanding the distinction between isomorphism and weak equivalence clarifies when strict equality is necessary versus when equivalence under deformation or partial structure preservation suffices for practical or theoretical applications.
Isomorphism Infographic
 libterm.com
libterm.com