A finite group is a mathematical structure consisting of a set with a finite number of elements equipped with an operation that satisfies closure, associativity, the existence of an identity element, and the existence of inverses for every element. These groups play a crucial role in various fields such as algebra, number theory, and physics by providing a framework to analyze symmetry and group actions. Explore the rest of the article to deepen your understanding of finite groups and their diverse applications.
Table of Comparison
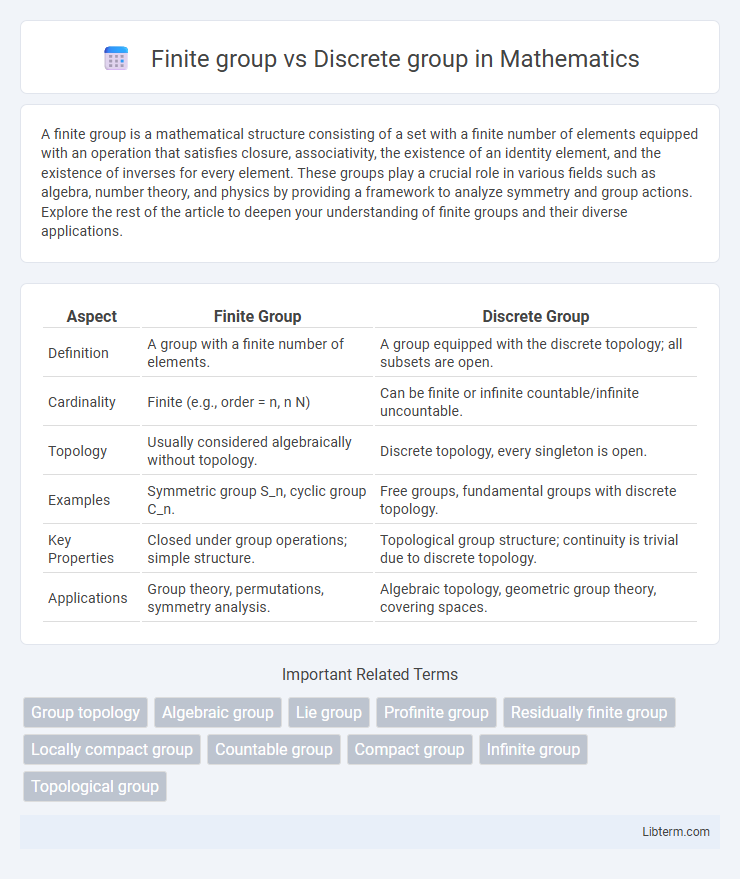
| Aspect | Finite Group | Discrete Group |
|---|---|---|
| Definition | A group with a finite number of elements. | A group equipped with the discrete topology; all subsets are open. |
| Cardinality | Finite (e.g., order = n, n N) | Can be finite or infinite countable/infinite uncountable. |
| Topology | Usually considered algebraically without topology. | Discrete topology, every singleton is open. |
| Examples | Symmetric group S_n, cyclic group C_n. | Free groups, fundamental groups with discrete topology. |
| Key Properties | Closed under group operations; simple structure. | Topological group structure; continuity is trivial due to discrete topology. |
| Applications | Group theory, permutations, symmetry analysis. | Algebraic topology, geometric group theory, covering spaces. |
Introduction to Finite and Discrete Groups
Finite groups consist of a limited number of elements with group operations defined by closure, associativity, identity, and invertibility. Discrete groups are characterized by having a discrete topology, meaning their elements are isolated points, often studied in geometric group theory and topology. The distinction lies in size and structure: finite groups are always discrete, but discrete groups can be infinite, playing crucial roles in symmetry analysis and crystallography.
Definitions: Finite Group vs Discrete Group
A finite group is a mathematical group consisting of a limited number of elements, where the group operation satisfies closure, associativity, identity, and invertibility, making its cardinality a finite integer. A discrete group is a topological group equipped with the discrete topology, meaning each singleton set is open, and it often arises in contexts where the group elements are isolated points in the space. While all finite groups are discrete due to their finite nature, discrete groups can be infinite, characterized by their topological properties rather than their size.
Key Properties of Finite Groups
Finite groups are algebraic structures with a limited number of elements, characterized by closure, associativity, identity, and invertibility properties. These groups exhibit a well-defined order, where the order of every element divides the group's order according to Lagrange's theorem. Unlike general discrete groups, finite groups have a finite cardinality that enables classification through group actions, Sylow theorems, and representation theory.
Key Properties of Discrete Groups
Discrete groups are characterized by having a topology in which each singleton set is open, allowing for isolated points without limit points. Unlike finite groups, which contain a limited number of elements, discrete groups can be infinite but maintain a discrete topology that enables local analysis using group actions on discrete spaces. Key properties include being countable or uncountable with isolated group elements, supporting group representations that act discontinuously, and having applications in geometry and number theory through discrete subgroups of Lie groups.
Structural Differences Between Finite and Discrete Groups
Finite groups have a limited number of elements, making their algebraic structure fully enumerable and often classified by well-known group orders and types such as cyclic or symmetric groups. Discrete groups, while not necessarily finite, possess a topology where points are isolated, allowing group operations to be continuous but defined on countable or infinite sets, resulting in more complex structural behaviors like infinite generators or intricate subgroup lattices. The main structural difference lies in finiteness restricting combinatorial complexity, whereas discreteness enables rich interactions between algebra and topology without the constraints of finite cardinality.
Examples of Finite and Discrete Groups
Finite groups include examples such as the symmetric group \( S_n \), which consists of all permutations of \( n \) elements, and cyclic groups \( \mathbb{Z}_n \), representing integers modulo \( n \). Discrete groups, often encountered in geometry and topology, include fundamental groups like the free group on two generators and infinite groups such as the integer lattice \( \mathbb{Z}^n \) acting as a discrete subgroup of Euclidean space. Both examples illustrate how finite groups have a limited number of elements, whereas discrete groups can be infinite but equipped with the discrete topology, ensuring isolated points.
Applications in Mathematics and Physics
Finite groups, characterized by a limited number of elements, are extensively applied in crystallography and quantum mechanics for modeling symmetrical structures and particle behaviors. Discrete groups, often infinite but countable, play a crucial role in number theory and the study of modular forms, influencing areas such as string theory and chaotic systems in physics. Both group types enable the classification of symmetries and facilitate the understanding of fundamental physical laws and mathematical invariants.
Topological Considerations: Discrete Groups as Topological Groups
Finite groups equipped with the discrete topology inherently satisfy the conditions of topological groups, as their topology makes all group operations continuous. Discrete groups, characterized by having every singleton set as an open set, serve as fundamental examples of topological groups where continuity of multiplication and inversion is trivial. The distinction lies in cardinality; finite groups are trivially discrete and thus topological, while infinite discrete groups extend this property to more complex, infinite algebraic structures without additional topological restrictions.
Homomorphisms and Subgroup Structures
Finite groups exhibit well-defined subgroup structures constrained by Lagrange's theorem, which dictates that the order of every subgroup divides the order of the group, influencing the nature of homomorphisms that preserve these divisors. Discrete groups, often infinite and endowed with the discrete topology, allow more flexible homomorphisms but may have complex or infinitely many subgroup structures not limited by finite order constraints. Homomorphisms in finite groups must respect finite orders and subgroup indices, while in discrete groups, the lack of topological restrictions permits broader mappings, significantly affecting the analysis of subgroup lattices and kernel structures.
Summary: Comparing Finite and Discrete Groups
Finite groups consist of a limited number of elements with algebraic structures that facilitate straightforward computation and classification, widely used in symmetry and combinatorial problems. Discrete groups, by contrast, are countable infinite or finite and play crucial roles in topology, geometric group theory, and crystallography, where their discrete topology influences group actions and space tessellations. The fundamental difference lies in cardinality and topological properties, with finite groups having a trivial topology and discrete groups possessing isolated points enabling richer spatial and algebraic interactions.
Finite group Infographic
 libterm.com
libterm.com