Non-commutative operations differ from commutative ones in that the order of applying them affects the outcome, which is crucial in fields like quantum mechanics and group theory. Understanding this concept provides insight into complex systems where sequence matters, such as matrix multiplication or certain algebraic structures. Explore the full article to deepen your grasp of non-commutative properties and their significance in various scientific disciplines.
Table of Comparison
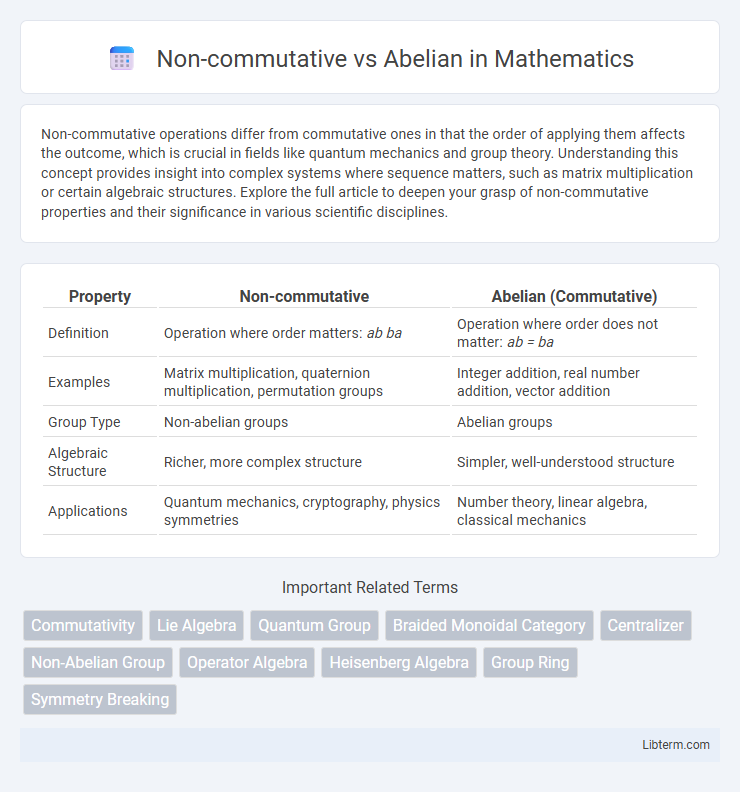
| Property | Non-commutative | Abelian (Commutative) |
|---|---|---|
| Definition | Operation where order matters: ab ba | Operation where order does not matter: ab = ba |
| Examples | Matrix multiplication, quaternion multiplication, permutation groups | Integer addition, real number addition, vector addition |
| Group Type | Non-abelian groups | Abelian groups |
| Algebraic Structure | Richer, more complex structure | Simpler, well-understood structure |
| Applications | Quantum mechanics, cryptography, physics symmetries | Number theory, linear algebra, classical mechanics |
Introduction to Non-Commutative and Abelian Structures
Non-commutative structures exhibit operations where the order of elements affects the result, such as matrix multiplication and certain group operations. Abelian structures, named after mathematician Niels Abel, feature commutative properties where the operation order does not change the outcome, exemplified by addition of real numbers and abelian groups. Understanding these foundational differences is crucial in abstract algebra, impacting areas like ring theory, group theory, and quantum mechanics.
Defining Commutativity: Key Mathematical Concepts
Commutativity in mathematics refers to the property where the order of applying an operation does not affect the outcome, typically expressed as a * b = b * a for elements a and b within a set. Non-commutative structures violate this property, meaning that a * b b * a, which is commonly observed in matrix multiplication and certain group operations. Abelian groups specifically embody commutativity, where every pair of elements satisfies the commutative law, distinguishing them fundamentally from non-Abelian groups in algebra and abstract algebraic systems.
Properties of Non-Commutative Groups
Non-commutative groups, also known as non-Abelian groups, exhibit the property where the group operation does not satisfy the commutative law, meaning for elements \(a\) and \(b\), \(ab \neq ba\) in general. These groups play a crucial role in advanced algebraic structures and theoretical physics due to their complex symmetry and transformation properties. Key characteristics include the presence of elements with non-trivial conjugacy classes and the potential for intricate subgroup structures, highlighting their significance in group theory and its applications.
Characteristics of Abelian Groups
Abelian groups are characterized by the commutative property, meaning the group operation satisfies a *b = b * a* for all elements *a* and *b*. These groups often exhibit simpler structural properties, with every subgroup being normal and the group's structure allowing for easier classification through direct products of cyclic groups. In contrast, non-commutative groups do not satisfy the commutative property, leading to more complex algebraic behaviors and richer symmetry structures in mathematical and physical applications.
Real-world Applications of Non-Commutative Systems
Non-commutative systems, unlike Abelian groups where operation order does not matter, play a crucial role in quantum mechanics, especially in the formulation of quantum operators and observables that do not commute, impacting measurement outcomes. These systems also appear in cryptographic algorithms such as non-commutative key exchange protocols, enhancing security beyond classical commutative schemes. Robotics and computer graphics exploit non-commutative matrix groups like the rotation group SO(3) to accurately model and manipulate spatial orientations.
Why Abelian Groups Matter in Mathematics
Abelian groups, characterized by their commutative property where the group operation satisfies \(a \cdot b = b \cdot a\), play a crucial role in various branches of mathematics including algebra, number theory, and topology. Their well-structured behavior simplifies the analysis of homomorphisms and enables the development of module theory, making them fundamental in solving linear equations and studying symmetry in mathematical systems. Unlike non-commutative groups, Abelian groups provide a foundational framework for concepts such as vector spaces, ring theory, and cohomology, underscoring their importance in both theoretical and applied mathematics.
Differences Between Non-Commutative and Abelian Groups
Non-commutative groups feature operations where the order of elements affects the result (xy yx), contrasting with Abelian groups where operations are commutative (xy = yx) for all elements x and y. In Abelian groups, the commutative property simplifies structure and analysis, enabling direct applications in areas like vector spaces and number theory. Non-commutative groups exhibit more complex behavior, critical in quantum mechanics and symmetry studies, due to their non-commuting elements and richer algebraic structure.
Common Examples: Non-Commutative vs. Abelian Groups
Non-commutative groups, also known as non-Abelian groups, include examples like the symmetric group \( S_3 \), which consists of permutations of three elements where the order of operations affects the outcome. Abelian groups, such as the integer group under addition \((\mathbb{Z}, +)\) or vector spaces under vector addition, exhibit commutative properties where the group operation is order-independent. The contrast between these groups highlights crucial differences in structure and symmetry relevant to fields like algebra, geometry, and physics.
Implications in Algebra and Beyond
Non-commutative algebra studies structures where the order of operations affects the outcome, contrasting with Abelian algebra where operations commute, granting symmetry and predictability. This fundamental difference impacts group theory, ring theory, and module theory, influencing the classification of groups and the behavior of algebraic systems. Beyond pure algebra, non-commutativity underpins quantum mechanics and cryptography, while Abelian properties simplify computations in coding theory and signal processing.
Future Perspectives: Advancements and Open Problems
Non-commutative algebraic structures offer promising advancements in quantum computing, cryptography, and non-classical logic systems, where Abelian models fall short due to their inherent commutativity constraints. Future research is focused on developing robust algorithms that leverage the complexity of non-commutative groups, aiming to solve open problems such as efficient factorization and representation theory in higher dimensions. Breakthroughs in non-commutative geometry and operator algebras are expected to deepen understanding of space-time at the quantum level, presenting new theoretical challenges and applications.
Non-commutative Infographic
 libterm.com
libterm.com