Sublevel sets consist of all points where a given function's value is less than or equal to a specified threshold, serving as crucial tools in optimization and mathematical analysis. Understanding sublevel sets helps you analyze function behavior, determine solution feasibility, and visualize constraint regions in various applications. Explore the rest of this article to delve deeper into the properties and uses of sublevel sets.
Table of Comparison
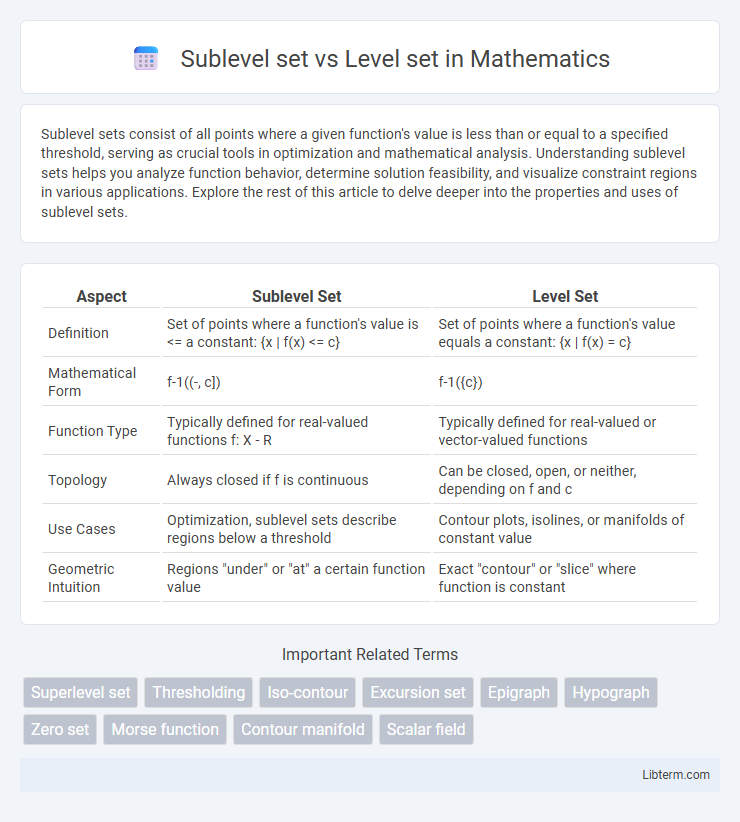
| Aspect | Sublevel Set | Level Set |
|---|---|---|
| Definition | Set of points where a function's value is <= a constant: {x | f(x) <= c} | Set of points where a function's value equals a constant: {x | f(x) = c} |
| Mathematical Form | f-1((-, c]) | f-1({c}) |
| Function Type | Typically defined for real-valued functions f: X - R | Typically defined for real-valued or vector-valued functions |
| Topology | Always closed if f is continuous | Can be closed, open, or neither, depending on f and c |
| Use Cases | Optimization, sublevel sets describe regions below a threshold | Contour plots, isolines, or manifolds of constant value |
| Geometric Intuition | Regions "under" or "at" a certain function value | Exact "contour" or "slice" where function is constant |
Introduction to Level Sets and Sublevel Sets
Level sets represent points where a function takes a constant value, forming contours or surfaces critical in shape analysis and image processing. Sublevel sets include all points where the function's value is less than or equal to a specified threshold, capturing regions bounded by level sets for topology and optimization studies. Understanding the distinction between level sets and sublevel sets enables advanced techniques in numerical analysis, computational geometry, and machine learning.
Mathematical Definitions: Level Sets vs Sublevel Sets
Level sets of a function f(x) are defined as the set of points where the function takes a constant value c, expressed as {x | f(x) = c}. Sublevel sets consist of all points where the function's value is less than or equal to c, denoted by {x | f(x) <= c}. These concepts are crucial in optimization and analysis, as level sets represent contour lines, while sublevel sets define regions bounded by these contours.
Geometric Interpretation
A sublevel set of a function consists of all points where the function value is less than or equal to a given threshold, forming a closed region that represents areas below a certain height in geometric analysis. In contrast, a level set comprises points where the function equals a specific value, typically forming curves or surfaces that act as boundaries between different sublevel sets. This geometric interpretation is crucial in fields like image processing and shape optimization, where level sets describe contours and sublevel sets characterize filled regions.
Key Differences Between Level and Sublevel Sets
Level sets represent points in a domain where a function equals a specific constant value, forming a contour or surface, while sublevel sets encompass all points where the function's value is less than or equal to that constant, creating an inclusive region. The key difference lies in the level set being a boundary or iso-value surface, and the sublevel set being a filled region that includes this boundary and all points below it. Sublevel sets are often used in optimization and topological data analysis to study regions below a threshold, whereas level sets are crucial for contour detection and interface tracking.
Visual Examples and Graphical Representation
Level sets represent points in a domain where a function equals a specific constant value, illustrated graphically as contour lines or curves in 2D plots. Sublevel sets consist of points where the function's value is less than or equal to a constant, often visualized as filled regions or areas below a contour line, highlighting the interior region beneath the level set boundary. Visual examples show level sets as precise isolines, while sublevel sets appear as shaded regions, emphasizing the function's accumulation up to the given threshold.
Applications in Mathematics and Science
Sublevel sets and level sets are crucial in mathematical analysis and scientific modeling, particularly in optimization, topology, and data visualization. Sublevel sets, defined as the sets where a function's value is less than or equal to a threshold, are extensively used in convex analysis and constraint optimization problems. Level sets, representing points where a function equals a constant value, play a vital role in differential equations, image processing, and shape modeling, enabling efficient contour detection and evolution in computational science.
Level Sets in Optimization Problems
Level sets represent the set of points where a function attains a specific constant value, playing a crucial role in optimization by helping visualize and analyze contour lines of objective functions. In optimization problems, level sets facilitate understanding constraints, capturing feasible regions or boundaries where decisions can be optimized efficiently. This approach aids gradient-based methods and nonlinear programming by providing geometric insights into function behavior and guiding convergence to optimal solutions.
Sublevel Sets in Feasibility Analysis
Sublevel sets consist of all points where a function's value is less than or equal to a given threshold, playing a crucial role in feasibility analysis by characterizing regions that satisfy inequality constraints. These sets help determine feasible regions within optimization problems by identifying all candidate solutions meeting the required bounds, thus facilitating constraint satisfaction checks. In contrast, level sets include points where the function equals a specific value, often providing boundary information rather than the entire feasible region.
Advantages and Limitations of Each Concept
Sublevel sets offer a comprehensive view of all points where a function remains below a specific threshold, making them valuable in optimization problems for identifying feasible regions. Level sets emphasize points where the function equals a constant, facilitating precise contour analysis and boundary detection in fields like image processing. While sublevel sets excel in capturing global properties, their limitation lies in potential complexity for high-dimensional data, whereas level sets provide exact contours but may struggle with noise sensitivity and disconnected regions.
Conclusion and Key Takeaways
Sublevel sets represent all points where a function's value is less than or equal to a specific threshold, capturing regions beneath a contour, whereas level sets consist solely of points where the function equals that exact threshold, forming precise contours. Sublevel sets provide insight into cumulative regions and are useful in optimization and analysis of function behavior over an interval. Level sets are crucial for identifying exact boundaries and are extensively applied in shape modeling, image processing, and numerical simulations.
Sublevel set Infographic
 libterm.com
libterm.com