The homology spectrum is a crucial concept in molecular biology, measuring the degree of similarity between DNA, RNA, or protein sequences to infer evolutionary relationships. Understanding the homology spectrum helps identify conserved regions that are essential for biological function and can guide your research in comparative genomics or protein engineering. Explore the rest of this article to dive deeper into how the homology spectrum informs scientific discoveries and practical applications.
Table of Comparison
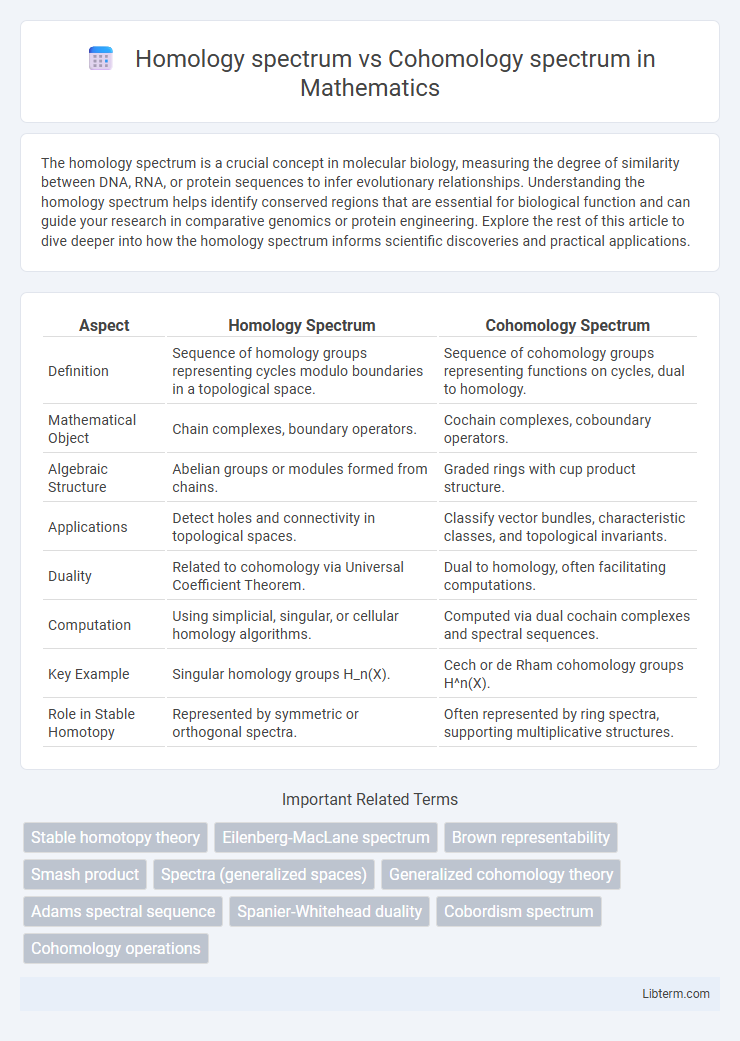
| Aspect | Homology Spectrum | Cohomology Spectrum |
|---|---|---|
| Definition | Sequence of homology groups representing cycles modulo boundaries in a topological space. | Sequence of cohomology groups representing functions on cycles, dual to homology. |
| Mathematical Object | Chain complexes, boundary operators. | Cochain complexes, coboundary operators. |
| Algebraic Structure | Abelian groups or modules formed from chains. | Graded rings with cup product structure. |
| Applications | Detect holes and connectivity in topological spaces. | Classify vector bundles, characteristic classes, and topological invariants. |
| Duality | Related to cohomology via Universal Coefficient Theorem. | Dual to homology, often facilitating computations. |
| Computation | Using simplicial, singular, or cellular homology algorithms. | Computed via dual cochain complexes and spectral sequences. |
| Key Example | Singular homology groups H_n(X). | Cech or de Rham cohomology groups H^n(X). |
| Role in Stable Homotopy | Represented by symmetric or orthogonal spectra. | Often represented by ring spectra, supporting multiplicative structures. |
Introduction to Homology and Cohomology Spectra
Homology spectra and cohomology spectra are fundamental tools in stable homotopy theory, representing generalized homology and cohomology theories through structured sequences of spaces or spectra. Homology spectra encode homological information by associating chain complexes to topological spaces, while cohomology spectra reflect cohomological operations and dualities, often serving as representing objects for cohomology theories like Eilenberg-MacLane spectra. These spectra facilitate computation and conceptual understanding of stable phenomena by bridging algebraic invariants and topological constructions.
Fundamental Concepts and Definitions
Homology spectrum refers to a sequence of homology groups associated with a topological space, capturing information about its cycles and boundaries across various dimensions, often represented by spectra in stable homotopy theory. Cohomology spectrum, on the other hand, involves cohomology groups that classify cochains and cocycles, equipping spaces with algebraic invariants reflecting their global structure via contravariant functors. Both concepts rely on fundamental notions such as chain complexes, exact sequences, and suspension, with spectra providing a framework to study stable phenomena and generalized (co)homology theories in algebraic topology.
Construction of Homology Spectrum
The construction of the homology spectrum involves applying a homology theory to the suspension spectrum of a space, producing a sequence of pointed spaces or spectra that encode stable homological information. This process relies on representing homology theories by Eilenberg-MacLane spectra or generalized homology theories corresponding to structured ring spectra. Unlike cohomology spectra, which are often constructed via function spectra or mapping spaces, homology spectra emphasize the geometric realization of cycles and bordism classes within stable homotopy categories.
Construction of Cohomology Spectrum
The construction of a cohomology spectrum involves defining a sequence of spaces and structure maps that represent a generalized cohomology theory, often using spectra in stable homotopy theory. Each level in the spectrum corresponds to the cohomological degree, and the structure maps induce suspension isomorphisms that align with the cohomological grading. Compared to homology spectra, which model homology theories through direct limits of spaces, cohomology spectra focus on contravariant functors and incorporate function spectra or dual constructions to capture cohomological information.
Key Differences between Homology and Cohomology Spectra
Homology spectra and cohomology spectra serve as fundamental tools in algebraic topology, with homology spectra focusing on classifying cycles and boundaries in topological spaces, while cohomology spectra emphasize the algebraic duals of these structures through cochains and coboundaries. A key difference lies in their algebraic interpretations: homology spectra yield invariants representing geometric features such as holes, whereas cohomology spectra provide ring structures that capture additional algebraic information and facilitate operations like cup product. Furthermore, cohomology spectra often admit richer computational frameworks and duality theorems, making them vital for analyzing the interplay between geometry and algebra in topological spaces.
Algebraic Structures: Modules and Algebras
Homology spectrum and cohomology spectrum both encode algebraic structures, with homology spectra typically forming modules over ring spectra, reflecting their role in measuring cycles and boundaries in topological spaces. Cohomology spectra naturally acquire richer algebraic structures, often endowed with cup products, making them commutative or associative algebras in stable homotopy categories. These distinctions highlight how homology manifests as module spectra capturing linear structures, while cohomology spectra provide algebraic frameworks that support multiplicative operations.
Applications in Stable Homotopy Theory
Homology spectrum and cohomology spectrum serve as fundamental tools for probing stable homotopy types through generalized (co)homology theories in stable homotopy theory. Homology spectra enable computations of stable homotopy groups by representing homology theories as spectra, such as Eilenberg-MacLane spectra for ordinary homology, while cohomology spectra model cohomology theories revealing dual algebraic structures that facilitate spectral sequence calculations like the Adams spectral sequence. These dual frameworks provide essential insights into the structure of ring spectra, module spectra, and enable the classification of stable phenomena in spaces and spectra, underpinning advances in chromatic homotopy theory and the study of structured ring spectra.
Computational Techniques for Spectra
Homology spectra and cohomology spectra serve as foundational tools in stable homotopy theory, where computational techniques such as spectral sequences, especially the Adams and Adams-Novikov spectral sequences, are crucial for analyzing their structure. Efficient algorithms often leverage chain complexes and the associated homological algebra to calculate homology groups, while cohomology spectra computations frequently utilize cohomological operations and dualities to extract algebraic invariants. Software tools like SageMath and specialized homotopy theory packages facilitate these calculations by implementing algorithmic spectral sequence constructions and automated handling of spectral data.
Notable Examples and Case Studies
Homology spectra and cohomology spectra play pivotal roles in stable homotopy theory, where the Eilenberg-MacLane spectrum serves as a notable example representing ordinary homology and cohomology theories with coefficients in an abelian group. The Brown-Peterson spectrum is a key case study demonstrating how homology spectra facilitate complex cobordism calculations, while the Anderson dual spectrum exemplifies the dual nature of cohomology spectra in generalized cohomology theories. These spectra encapsulate algebraic invariants critical for analyzing topological spaces, bridging homological and cohomological perspectives in algebraic topology.
Current Research and Open Questions
Homology spectra and cohomology spectra are central objects in stable homotopy theory, with current research exploring their roles in generalized cohomology theories and chromatic homotopy theory. Recent work investigates computational techniques for homotopy groups of spectra, including equivariant and motivic versions, while understanding duality phenomena between homology and cohomology spectra remains a key open question. Advances in higher category theory and spectral algebraic geometry also drive new insights into the interplay between these spectra and structured ring spectra, stimulating ongoing developments in the field.
Homology spectrum Infographic
 libterm.com
libterm.com