Transpose refers to the operation of flipping a matrix over its diagonal, effectively switching its rows with columns. This transformation is essential in various fields such as mathematics, computer science, and data analysis for manipulating and comparing datasets. Discover how the concept of transpose plays a crucial role in your data processing and mathematical applications by exploring the rest of this article.
Table of Comparison
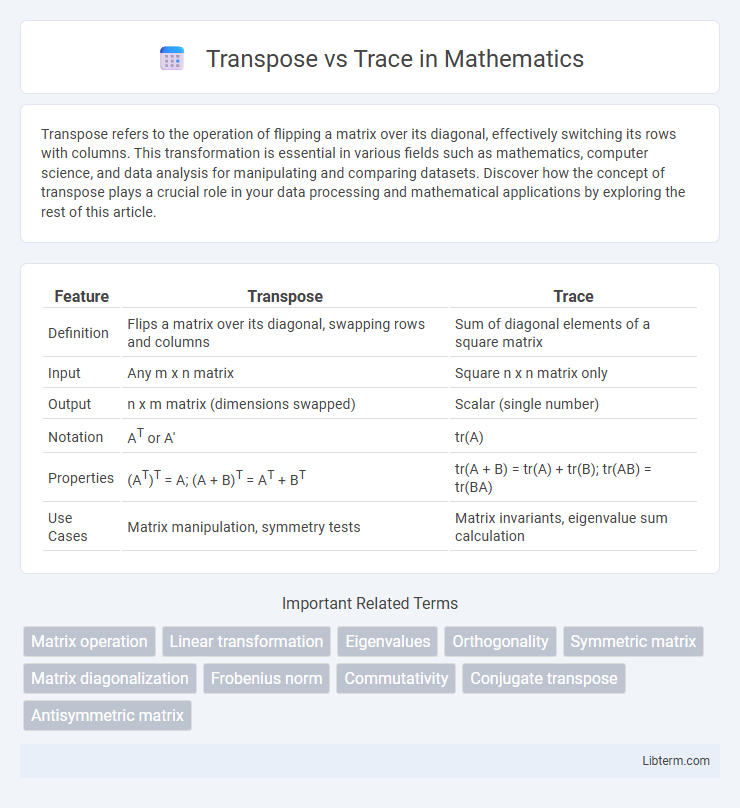
| Feature | Transpose | Trace |
|---|---|---|
| Definition | Flips a matrix over its diagonal, swapping rows and columns | Sum of diagonal elements of a square matrix |
| Input | Any m x n matrix | Square n x n matrix only |
| Output | n x m matrix (dimensions swapped) | Scalar (single number) |
| Notation | AT or A' | tr(A) |
| Properties | (AT)T = A; (A + B)T = AT + BT | tr(A + B) = tr(A) + tr(B); tr(AB) = tr(BA) |
| Use Cases | Matrix manipulation, symmetry tests | Matrix invariants, eigenvalue sum calculation |
Introduction to Matrix Operations
Matrix transpose reconfigures an m x n matrix by flipping its rows and columns, converting it into an n x m matrix, which is fundamental in linear algebra for reshaping data and facilitating operations like matrix multiplication. The trace of a square matrix is the sum of its diagonal elements, serving as a critical scalar value that often represents properties such as the matrix's invariance under similarity transformations. Understanding the distinctions and applications of transpose and trace is essential for effective manipulation and analysis of matrices in fields like computer graphics, physics, and data science.
Defining Transpose of a Matrix
The transpose of a matrix is defined by flipping the matrix over its diagonal, converting the row indices of elements into column indices and vice versa. This operation transforms an mxn matrix into an nxm matrix, where each element A[i][j] in the original matrix becomes A[j][i] in the transposed matrix. Unlike the trace, which sums diagonal elements of a square matrix, the transpose repositions all elements without altering their values.
Understanding the Trace of a Matrix
The trace of a matrix is the sum of its diagonal elements, providing a scalar value that often represents important properties in linear algebra such as the sum of eigenvalues. Unlike the transpose, which reorganizes the matrix by flipping it over its diagonal, the trace remains invariant under transposition, meaning the trace of a matrix and its transpose are identical. Understanding the trace is crucial in applications across physics, computer science, and statistics, where it helps measure matrix characteristics like matrix invariants and the outcome of matrix multiplications.
Key Differences: Transpose vs Trace
Transpose transforms a matrix by swapping its rows and columns, effectively flipping it over its diagonal, while trace calculates the sum of the diagonal elements of a square matrix. The transpose operation results in a matrix of the same dimensions flipped, but the trace produces a single scalar value. Transpose is used in matrix manipulation and linear transformations, whereas trace is often applied in eigenvalue problems and matrix invariants.
Mathematical Properties of Transpose
The transpose of a matrix involves flipping it over its diagonal, converting rows into columns, and preserving dimensions for square matrices. Key mathematical properties include the relation (AT)T = A, the linearity property (A + B)T = AT + BT, and the product rule (AB)T = BTAT, which highlights the reversal of multiplication order. These properties enable simplification in matrix equations, proofs, and play a crucial role in concepts such as symmetric and orthogonal matrices.
Mathematical Properties of Trace
The trace of a matrix is the sum of its diagonal elements, invariant under cyclic permutations, making it a crucial tool in linear algebra for characterizing matrix similarity and eigenvalue sums. Unlike transpose, which reflects a matrix across its main diagonal, the trace reduces a matrix to a scalar preserving key spectral properties. This scalar invariance under similarity transformations helps in simplifying complex matrix operations and plays a vital role in fields like quantum mechanics and system theory.
Applications of Transpose in Linear Algebra
The transpose of a matrix plays a crucial role in solving systems of linear equations, transforming matrix equations into more manageable forms and enabling efficient computation of solutions. It is essential in defining symmetric and orthogonal matrices, which are widely used in optimization problems and quantum mechanics. Transpose operations also facilitate the computation of dot products and projections, fundamental in computer graphics and machine learning algorithms.
Applications of Trace in Mathematics
The trace of a matrix, defined as the sum of its diagonal elements, plays a crucial role in linear algebra and other mathematical fields by providing a scalar invariant under similarity transformations. It is widely applied in characterizing matrix properties such as eigenvalues, since the trace equals the sum of eigenvalues, and in quantum mechanics for describing state operators. The trace function is also fundamental in optimization problems, differential geometry, and statistics, particularly in the calculation of matrix derivatives and in the study of covariance matrices.
Computational Complexity: Transpose vs Trace
The computational complexity of the transpose operation on an n x m matrix involves rearranging elements, typically requiring O(nm) time as each element must be repositioned. In contrast, computing the trace of an n x n square matrix involves summing only the n diagonal elements, resulting in a linear time complexity of O(n). Efficient implementations leverage the inherent difference, with trace computations being significantly less resource-intensive than performing a full matrix transpose.
Summary and Practical Implications
Transpose changes the orientation of a matrix by flipping it over its diagonal, converting rows into columns, which is essential in tasks involving matrix reshaping and linear transformations. Trace calculates the sum of diagonal elements, offering a scalar that reflects key properties like the matrix's eigenvalue sum, useful in performance metrics and stability analysis. Understanding when to apply transpose versus trace enhances efficiency in algorithms such as matrix multiplication, system solving, and optimization problems.
Transpose Infographic
 libterm.com
libterm.com