Matrix norm measures the size or length of a matrix, providing a quantitative way to evaluate its magnitude. Common types include the Frobenius norm, which sums the squares of all entries, and operator norms, which reflect the matrix's action on vectors. Explore the rest of this article to understand how different matrix norms apply to your mathematical and computational tasks.
Table of Comparison
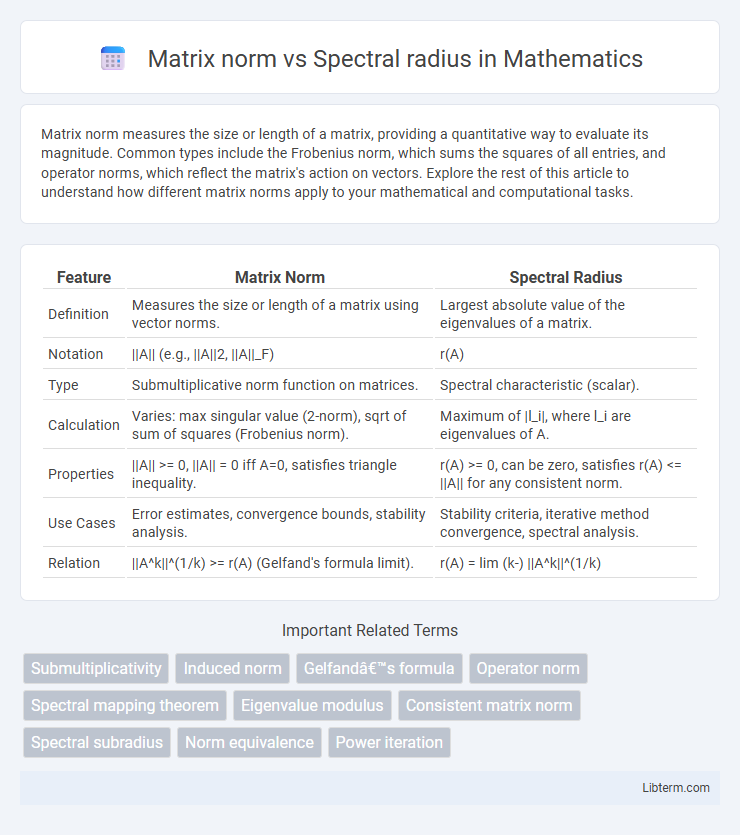
| Feature | Matrix Norm | Spectral Radius |
|---|---|---|
| Definition | Measures the size or length of a matrix using vector norms. | Largest absolute value of the eigenvalues of a matrix. |
| Notation | ||A|| (e.g., ||A||2, ||A||_F) | r(A) |
| Type | Submultiplicative norm function on matrices. | Spectral characteristic (scalar). |
| Calculation | Varies: max singular value (2-norm), sqrt of sum of squares (Frobenius norm). | Maximum of |l_i|, where l_i are eigenvalues of A. |
| Properties | ||A|| >= 0, ||A|| = 0 iff A=0, satisfies triangle inequality. | r(A) >= 0, can be zero, satisfies r(A) <= ||A|| for any consistent norm. |
| Use Cases | Error estimates, convergence bounds, stability analysis. | Stability criteria, iterative method convergence, spectral analysis. |
| Relation | ||A^k||^(1/k) >= r(A) (Gelfand's formula limit). | r(A) = lim (k-) ||A^k||^(1/k) |
Introduction to Matrix Norm and Spectral Radius
Matrix norm quantifies the size or length of a matrix, commonly used norms include the Frobenius norm and operator norm, which measure the overall magnitude of matrix elements or its effect on vectors. Spectral radius refers to the largest absolute value of a matrix's eigenvalues, providing critical insight into the matrix's stability and long-term behavior in iterative processes. Understanding these concepts is essential in fields like numerical analysis, where matrix norm bounds convergence rates and spectral radius dictates stability criteria.
Definitions: Matrix Norm and Spectral Radius
The matrix norm is a function that assigns a non-negative scalar to a matrix, measuring its "size" or "length" based on specific criteria such as the Frobenius norm or the induced p-norm. The spectral radius of a matrix is defined as the largest absolute value among its eigenvalues, reflecting the matrix's dominant eigenvalue magnitude. While matrix norms provide bounds on matrix behavior in vector transformations, the spectral radius directly quantifies the maximum growth rate in iterative processes or powers of the matrix.
Types of Matrix Norms
Matrix norms measure the size or length of matrices and include types such as the Frobenius norm, induced p-norms (like the 1-norm, infinity norm, and 2-norm), and the max norm. The spectral radius, defined as the largest absolute eigenvalue of a matrix, differs from norms because it captures growth rates of matrix powers rather than matrix size in vector space terms. Induced matrix norms, particularly the 2-norm, are closely related to the spectral radius since the spectral radius is bounded above by any consistent matrix norm.
Calculating the Spectral Radius
Calculating the spectral radius involves determining the largest absolute value among the eigenvalues of a matrix, which provides critical insight into the matrix's behavior in iterative processes and stability analysis. Unlike matrix norms that measure size in a consistent manner across all entries, the spectral radius specifically targets eigenvalues, making it essential for assessing convergence properties in numerical algorithms. Efficient computation of the spectral radius often utilizes the power iteration method or eigenvalue decomposition techniques for large or sparse matrices.
Relationship Between Matrix Norm and Spectral Radius
The spectral radius of a matrix, defined as the largest absolute value of its eigenvalues, is always bounded above by any consistent matrix norm, ensuring r(A) <= ||A|| for matrix A. This relationship implies that while the matrix norm can provide an upper bound for the spectral radius, it may not tightly characterize the spectral behavior, especially for non-normal matrices. Understanding this inequality is crucial in numerical linear algebra for stability analysis, iterative methods, and convergence guarantees.
Key Differences: Matrix Norm vs Spectral Radius
Matrix norm measures the size or length of a matrix in terms of vector space, capturing bounds on matrix behavior with properties like submultiplicativity and various types (e.g., Frobenius, operator norms). Spectral radius specifically quantifies the largest absolute eigenvalue of a matrix, providing insight into stability and convergence in iterative processes. Key differences include matrix norm being a broader measure with multiple definitions and spectral radius explicitly describing eigenvalue magnitude, crucial for analyzing matrix powers and system dynamics.
Properties and Theorems
Matrix norms quantify the size of a matrix through sub-multiplicative and consistency properties, with the induced norm satisfying \( \|AB\| \leq \|A\| \|B\| \). The spectral radius, defined as the maximum absolute value of eigenvalues \( \rho(A) = \max |\lambda_i| \), is bounded by any matrix norm via the Gelfand formula \( \rho(A) = \lim_{k \to \infty} \|A^k\|^{1/k} \). Key theorems include the spectral radius inequality \( \rho(A) \leq \|A\| \) for any consistent norm and the Perron-Frobenius theorem, which guarantees a positive eigenvalue equal to the spectral radius for positive matrices.
Applications in Numerical Analysis
Matrix norms provide essential bounds for error estimation and convergence analysis in iterative numerical methods, while spectral radius directly indicates stability properties of matrices in solving linear systems. In numerical analysis, spectral radius helps determine the convergence rate of power iteration and other eigenvalue algorithms, whereas matrix norms facilitate the evaluation of approximation errors and conditioning of problems. Efficient numerical solutions rely on combining spectral radius assessments with matrix norm bounds to optimize algorithm performance and ensure numerical stability.
Matrix Norm and Spectral Radius in Stability Analysis
Matrix norm quantifies the size or length of a matrix, providing bounds on vector transformations and playing a critical role in stability analysis by measuring convergence rates in iterative methods. Spectral radius, defined as the largest absolute eigenvalue of a matrix, directly determines stability in linear dynamical systems since a spectral radius less than one implies asymptotic stability. Comparing both, spectral radius offers precise stability conditions, while matrix norms provide efficient, computable upper bounds crucial for estimating system behavior in numerical algorithms.
Summary and Conclusions
Matrix norm quantifies the largest extent a matrix can stretch a vector in a given normed space, providing a bound on matrix behavior, while spectral radius measures the maximum absolute value of its eigenvalues, directly indicating asymptotic stability and convergence rates. Norms are submultiplicative and offer upper bounds on the spectral radius, yet the spectral radius gives precise insight into iterative processes and stability criteria that norms alone cannot fully capture. Understanding the interplay between matrix norms and spectral radius is crucial for stability analysis, numerical methods, and optimization problems in applied linear algebra.
Matrix norm Infographic
 libterm.com
libterm.com