A complex manifold is a topological space resembling complex Euclidean space near each point, equipped with a compatible complex structure that allows for complex differentiability. These structures play a crucial role in various fields such as complex analysis, algebraic geometry, and theoretical physics. Explore the rest of the article to deepen your understanding of complex manifolds and their significant applications.
Table of Comparison
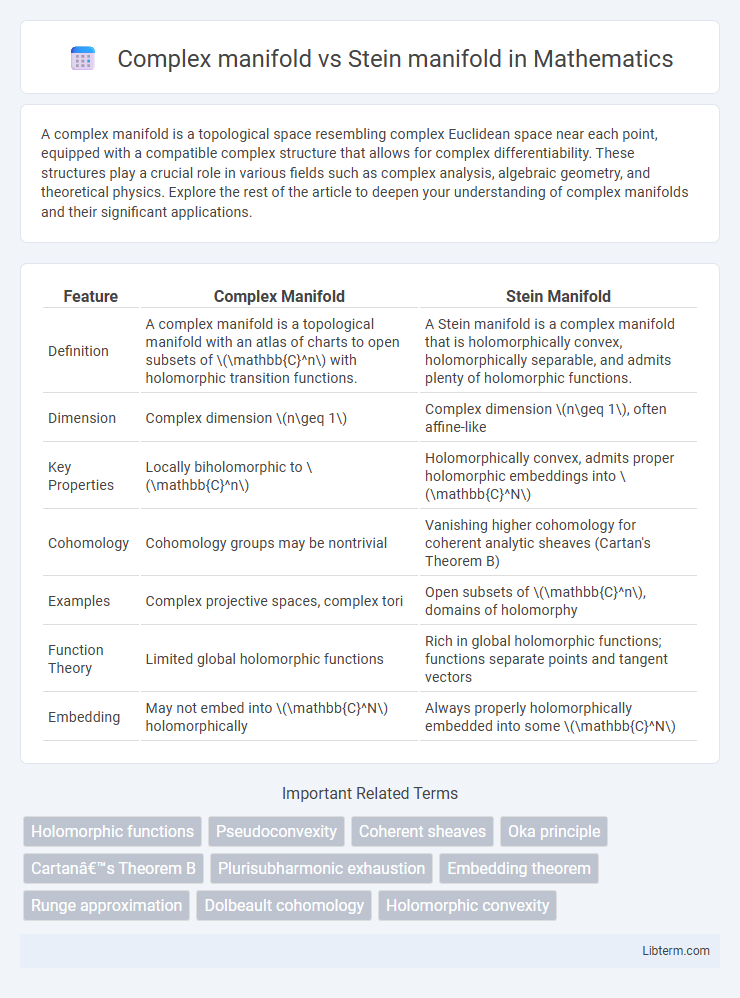
| Feature | Complex Manifold | Stein Manifold |
|---|---|---|
| Definition | A complex manifold is a topological manifold with an atlas of charts to open subsets of \(\mathbb{C}^n\) with holomorphic transition functions. | A Stein manifold is a complex manifold that is holomorphically convex, holomorphically separable, and admits plenty of holomorphic functions. |
| Dimension | Complex dimension \(n\geq 1\) | Complex dimension \(n\geq 1\), often affine-like |
| Key Properties | Locally biholomorphic to \(\mathbb{C}^n\) | Holomorphically convex, admits proper holomorphic embeddings into \(\mathbb{C}^N\) |
| Cohomology | Cohomology groups may be nontrivial | Vanishing higher cohomology for coherent analytic sheaves (Cartan's Theorem B) |
| Examples | Complex projective spaces, complex tori | Open subsets of \(\mathbb{C}^n\), domains of holomorphy |
| Function Theory | Limited global holomorphic functions | Rich in global holomorphic functions; functions separate points and tangent vectors |
| Embedding | May not embed into \(\mathbb{C}^N\) holomorphically | Always properly holomorphically embedded into some \(\mathbb{C}^N\) |
Introduction to Complex Manifolds
Complex manifolds are topological spaces locally modeled on open subsets of complex Euclidean spaces \(\mathbb{C}^n\), equipped with holomorphic transition maps, providing a natural generalization of complex curves to higher dimensions. Stein manifolds are a distinguished class of complex manifolds characterized by holomorphic convexity, holomorphic separability, and the existence of plenty of holomorphic functions, making them analogues of affine varieties in algebraic geometry. The study of complex manifolds introduces foundational concepts such as holomorphic charts, complex structures, and dimensionality, establishing the groundwork for analyzing more specialized structures like Stein manifolds.
Defining Stein Manifolds
A Stein manifold is a complex manifold that is holomorphically convex, holomorphically separable, and admits a proper holomorphic embedding into some complex Euclidean space \(\mathbb{C}^n\). Unlike general complex manifolds, Stein manifolds possess a rich supply of global holomorphic functions that separate points and provide local coordinates. These properties make Stein manifolds the complex analytic analogues of affine varieties in algebraic geometry, emphasizing their role in function theory on complex manifolds.
Key Properties of Complex Manifolds
Complex manifolds are topological spaces locally modeled on open subsets of \(\mathbb{C}^n\) with holomorphic transition maps, allowing complex-analytic structures without requiring global holomorphic function abundance. Stein manifolds are special complex manifolds characterized by holomorphic convexity, the existence of sufficiently many global holomorphic functions, and they satisfy the separation of points and tangent vectors via holomorphic functions, making them the complex-analytic analogs of affine varieties. Key properties of complex manifolds include dimension, complex structure, holomorphic tangent bundles, and local holomorphic coordinates, while Stein manifolds further possess the cohomological vanishing properties \(H^q(X, \mathcal{O}) = 0\) for \(q > 0\) that facilitate function theory and embedding theorems.
Essential Characteristics of Stein Manifolds
Stein manifolds are complex manifolds characterized by their holomorphic convexity, holomorphic separability, and the existence of plenty of global holomorphic functions, allowing proper embedding into complex Euclidean spaces. Unlike general complex manifolds, Stein manifolds satisfy the property that every coherent analytic sheaf is generated by global sections, ensuring rich function theory. These essential characteristics make Stein manifolds the natural analogs of affine algebraic varieties in complex analysis and contribute to their fundamental role in Oka theory and several complex variables.
Holomorphic Functions: Differences in Behavior
Holomorphic functions on complex manifolds exhibit varying behaviors compared to those on Stein manifolds, where the latter supports a rich supply of global holomorphic functions allowing for exhaustive approximation and complex analytic structures. Complex manifolds may lack sufficient holomorphic functions globally, restricting the ability to separate points or embed into complex Euclidean space, unlike Stein manifolds that satisfy these properties by definition. Stein manifolds serve as the natural setting for solving the \( \bar{\partial} \)-problem and ensure coherence of the sheaf of holomorphic functions, leading to powerful function-theoretic and cohomological results absent in general complex manifolds.
Topological and Analytic Distinctions
Complex manifolds are smooth manifolds equipped with a complex structure, allowing holomorphic coordinate transitions, whereas Stein manifolds are a special class of complex manifolds characterized by properties such as holomorphic convexity and the existence of plenty of global holomorphic functions. Topologically, Stein manifolds are holomorphically convex and admit proper holomorphic embeddings into complex Euclidean spaces, which is not necessarily true for general complex manifolds that may lack such embedding properties or holomorphic convexity. Analytically, Stein manifolds exhibit the property that every coherent analytic sheaf is generated by its global sections, reflecting their rich function theory and making them analogous to affine varieties in algebraic geometry, while general complex manifolds may fail to have such strong analytic structures.
Embedding Theorems: Stein vs. General Complex Manifolds
Stein manifolds are characterized by their ability to be holomorphically embedded into complex Euclidean spaces \(\mathbb{C}^n\) due to their rich function theory and strict pseudoconvexity, as established by the embedding theorems of Narasimhan and Bishop. In contrast, general complex manifolds lack such global embedding properties because they may not admit sufficient holomorphic functions to separate points and tangent vectors, preventing the construction of proper embeddings into \(\mathbb{C}^n\). The embedding theorems for Stein manifolds leverage their exhaustion by strictly plurisubharmonic functions, a property absent in arbitrary complex manifolds, making Stein manifolds notably embeddable and Stein's embedding theorem a cornerstone in several complex variables and complex geometry.
Examples Illustrating Both Manifolds
Complex manifolds include varieties like complex projective spaces and complex tori, exhibiting rich geometric structures but often lacking global holomorphic functions. Stein manifolds, typified by affine complex spaces such as \(\mathbb{C}^n\) and domains of holomorphy, are characterized by their abundance of holomorphic functions and topological properties like holomorphic convexity. For instance, while \(\mathbb{C}P^n\) is a compact complex manifold not Stein due to its lack of global holomorphic functions, domains like the unit ball in \(\mathbb{C}^n\) serve as prototypical Stein manifolds with exhaustive holomorphic function algebras.
Applications in Complex Geometry and Analysis
Complex manifolds serve as foundational spaces in complex geometry, supporting structures like holomorphic vector bundles and enabling the study of complex differential equations. Stein manifolds, characterized by their holomorphic convexity and abundance of global holomorphic functions, facilitate powerful analytic techniques such as the solution of the $\bar{\partial}$-problem and Runge approximation. These properties make Stein manifolds essential tools for embedding theorems, function theory, and cohomological vanishing results in several complex variables and complex analytic geometry.
Summary: Choosing Between Complex and Stein Manifolds
Complex manifolds are smooth, complex-analytic spaces that provide a broad framework for studying complex geometry and differential structures, while Stein manifolds are a special class of complex manifolds characterized by being holomorphically convex and admitting plenty of holomorphic functions. Stein manifolds serve as the complex-analytic analogue of affine varieties and are particularly useful for problems requiring strong function theory and cohomological vanishing theorems, making them ideal in several complex variables and embedding problems. Choosing between complex and Stein manifolds depends on the need for analytic flexibility versus topological generality, with Stein manifolds favored when constructing embeddings into complex Euclidean spaces or solving extension problems for holomorphic functions.
Complex manifold Infographic
 libterm.com
libterm.com