Quotient space is a fundamental concept in topology and linear algebra, formed by partitioning a space into equivalence classes under a given relation. This construction simplifies complex structures by identifying points that share a specific property, influencing properties like continuity and compactness in the resulting space. Discover how understanding quotient spaces can enhance your grasp of advanced mathematical frameworks by reading the rest of this article.
Table of Comparison
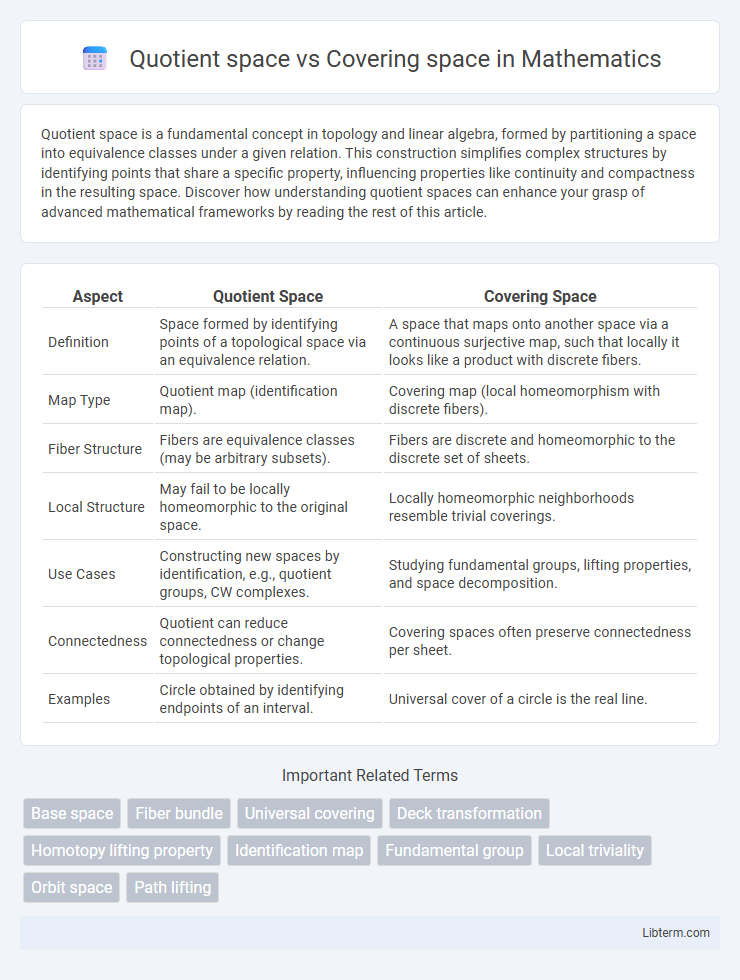
| Aspect | Quotient Space | Covering Space |
|---|---|---|
| Definition | Space formed by identifying points of a topological space via an equivalence relation. | A space that maps onto another space via a continuous surjective map, such that locally it looks like a product with discrete fibers. |
| Map Type | Quotient map (identification map). | Covering map (local homeomorphism with discrete fibers). |
| Fiber Structure | Fibers are equivalence classes (may be arbitrary subsets). | Fibers are discrete and homeomorphic to the discrete set of sheets. |
| Local Structure | May fail to be locally homeomorphic to the original space. | Locally homeomorphic neighborhoods resemble trivial coverings. |
| Use Cases | Constructing new spaces by identification, e.g., quotient groups, CW complexes. | Studying fundamental groups, lifting properties, and space decomposition. |
| Connectedness | Quotient can reduce connectedness or change topological properties. | Covering spaces often preserve connectedness per sheet. |
| Examples | Circle obtained by identifying endpoints of an interval. | Universal cover of a circle is the real line. |
Introduction to Topological Spaces
Quotient spaces in topology involve partitioning a topological space into equivalence classes and endowing the set of these classes with the quotient topology, allowing for the study of complicated spaces through simpler identification processes. Covering spaces consist of a continuous surjective map from a topological space that "covers" another space, locally resembling a product space, which is essential in analyzing fundamental groups and lifting properties. Both concepts serve as foundational tools in understanding the structure and classification of topological spaces, particularly in algebraic topology and geometric group theory.
Defining Quotient Spaces
Quotient spaces are defined by partitioning a topological space into equivalence classes via an equivalence relation and endowing the set of these classes with the quotient topology, which is the finest topology making the natural projection map continuous. This construction contrasts with covering spaces, where a space maps onto another through a local homeomorphism that 'covers' the base space with discrete fibers. Understanding quotient spaces involves analyzing how identification of points alters the topological and algebraic properties, affecting invariants such as homotopy and homology groups.
Understanding Covering Spaces
Covering spaces are topological spaces that map continuously onto a base space such that each point in the base space has an open neighborhood evenly covered by the map, meaning it is homeomorphic to a disjoint union of open sets in the covering space. This concept is central in algebraic topology for studying fundamental groups, as covering spaces correspond to subgroups of the base space's fundamental group, enabling classification via group actions. A quotient space, in contrast, is formed by identifying points in a topological space according to an equivalence relation, which may not preserve local homeomorphisms and thus differs fundamentally from the structure-preserving properties of covering spaces.
Fundamental Differences: Quotient vs Covering Spaces
Quotient spaces are formed by identifying points in a topological space according to an equivalence relation, resulting in a space that often has singularities or modified topology. Covering spaces involve a continuous surjective map from a "cover" space onto a base space, where each point in the base has an evenly covered neighborhood, maintaining local homeomorphism. The fundamental difference lies in that quotient spaces modify the original space by collapsing subsets, while covering spaces unfold the base space into layers preserving local structure.
Construction Methods for Quotient Spaces
Quotient spaces are constructed by partitioning a topological space into equivalence classes defined by an equivalence relation, and then endowing the set of classes with the quotient topology that makes the natural projection map continuous and surjective. This construction method contrasts with covering spaces, which are created via continuous surjective maps that are locally homeomorphic projections, often involving lifting paths and homotopy conditions rather than equivalence relations. The quotient space construction emphasizes collapsing subsets into points, while covering space construction involves unfolding spaces to create locally trivial fiber bundles.
Construction Methods for Covering Spaces
Covering spaces are constructed using methods such as lifting properties of paths and loops, fiber bundles, and universal covers derived from the fundamental group of the base space. Quotient spaces involve identifying points via an equivalence relation, often lacking the local triviality required for covering spaces. The construction of covering spaces typically requires a discrete and evenly covered projection map, unlike quotients which may produce singularities or non-local homeomorphisms.
Properties and Examples of Quotient Spaces
Quotient spaces are formed by partitioning a topological space into equivalence classes, identified by a surjective map that glues points according to an equivalence relation, often used to create new spaces with simpler or desired properties. Key properties include the preservation of continuous functions under the quotient map and the formation of topological spaces that may lose separation axioms, such as being non-Hausdorff, exemplified by the identification space of a square's edges producing a torus. Unlike covering spaces that involve local homeomorphic projections, quotient spaces emphasize global identification, as demonstrated in the construction of the Mobius strip by identifying opposite edges of a rectangle with a twist.
Properties and Examples of Covering Spaces
Covering spaces feature a continuous surjective map p: E - B where each point in B has an open neighborhood evenly covered by disjoint open sets in E, forming a local homeomorphism. Properties include path lifting, unique lifting of homotopies, and a fundamental group action that relates the total space E to the base space B. Classic examples of covering spaces are the map from the real line R to the circle S1 via the exponential function and the n-fold covering of the circle S1 given by z - zn in the complex plane.
Applications in Topology and Geometry
Quotient spaces simplify complex topological structures by identifying points under an equivalence relation, enabling the study of spaces such as projective planes and orbifolds in geometry. Covering spaces provide powerful tools for analyzing fundamental groups and lifting properties, essential in classifying topological spaces and solving problems in Riemann surface theory. Both concepts facilitate the examination of global properties through local analysis, playing crucial roles in fiber bundle theory and algebraic topology applications.
Choosing Between Quotient and Covering Spaces
Choosing between quotient spaces and covering spaces depends on the desired topological properties and the complexity of the space involved. Quotient spaces collapse specific subsets or equivalence classes into single points, simplifying structure but potentially introducing singularities, while covering spaces provide a locally homeomorphic projection that preserves local topology and enables analysis of fundamental groups. Use quotient spaces to identify or glue parts of a space compactly, whereas covering spaces are preferable for studying lifting properties, deck transformations, and unraveling complicated topologies into simpler, well-behaved layers.
Quotient space Infographic
 libterm.com
libterm.com