Product topology is a fundamental concept in topology, where the topological structure on a product of spaces is defined using the individual topologies of each factor. This topology is generated by the basis consisting of all products of open sets from the component spaces, capturing continuity and convergence properties effectively. Explore the rest of the article to deepen your understanding of product topology and its applications.
Table of Comparison
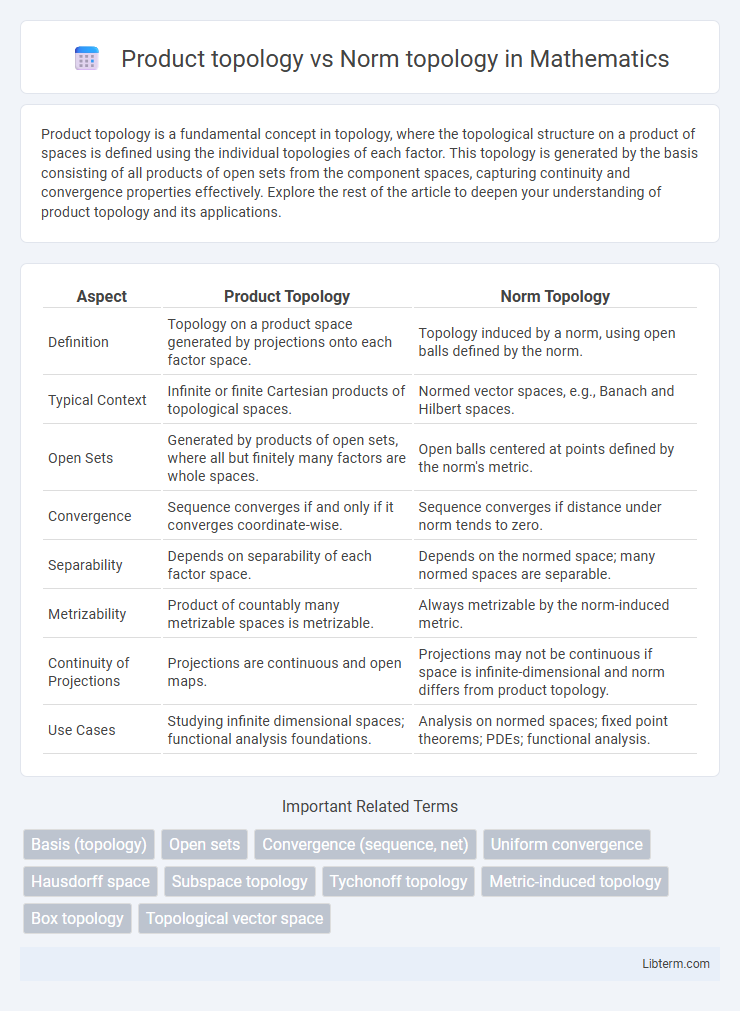
| Aspect | Product Topology | Norm Topology |
|---|---|---|
| Definition | Topology on a product space generated by projections onto each factor space. | Topology induced by a norm, using open balls defined by the norm. |
| Typical Context | Infinite or finite Cartesian products of topological spaces. | Normed vector spaces, e.g., Banach and Hilbert spaces. |
| Open Sets | Generated by products of open sets, where all but finitely many factors are whole spaces. | Open balls centered at points defined by the norm's metric. |
| Convergence | Sequence converges if and only if it converges coordinate-wise. | Sequence converges if distance under norm tends to zero. |
| Separability | Depends on separability of each factor space. | Depends on the normed space; many normed spaces are separable. |
| Metrizability | Product of countably many metrizable spaces is metrizable. | Always metrizable by the norm-induced metric. |
| Continuity of Projections | Projections are continuous and open maps. | Projections may not be continuous if space is infinite-dimensional and norm differs from product topology. |
| Use Cases | Studying infinite dimensional spaces; functional analysis foundations. | Analysis on normed spaces; fixed point theorems; PDEs; functional analysis. |
Introduction to Topological Concepts
Product topology arises from the Cartesian product of topological spaces, where the open sets are defined as the product of open sets in each coordinate space, preserving continuity across multiple dimensions. Norm topology, derived from a norm on a vector space, defines open sets based on the norm-induced metric, emphasizing the structure of vector spaces with notions of length and distance. Understanding these topologies is fundamental in analysis and geometry, as product topology handles multi-dimensional continuity, while norm topology informs convergence and continuity in normed vector spaces.
Defining Product Topology
The product topology on a Cartesian product of topological spaces is defined as the coarsest topology that makes all projection maps continuous, generated by the basis consisting of all products of open sets from the factor spaces. In contrast, the norm topology on a product space equipped with a norm arises from the metric induced by the norm, focusing on convergence related to the norm's induced distance. Understanding the product topology is crucial for analyzing continuity and convergence in infinite-dimensional spaces where the norm topology may differ significantly in structure and properties.
Understanding Norm Topology
Norm topology on a vector space is induced by a norm, defining open sets through norm-based open balls that measure vector magnitude and distance. Product topology, formed from the Cartesian product of topological spaces, uses the weakest topology making all projection maps continuous but does not inherently rely on a norm. Understanding norm topology involves grasping how norm-induced metric shapes convergence, continuity, and compactness, providing a concrete geometric intuition absent in abstract product topologies.
Fundamental Differences Between Product and Norm Topologies
The product topology is defined as the coarsest topology that makes all projection maps continuous, constructed from the Cartesian product of topological spaces and emphasizing coordinate-wise convergence. In contrast, the norm topology arises from a norm on a vector space and induces a metric, focusing on convergence with respect to the norm's induced distance. Fundamental differences include that product topology generally allows separate treatment of each coordinate while norm topology provides a unified, metric-based structure controlling overall vector magnitude and direction.
Construction of Product Topology
The construction of the product topology involves equipping the Cartesian product of a family of topological spaces with the coarsest topology that makes all the canonical projection maps continuous. This topology is generated by taking as a subbase the inverse images of open sets from each factor space under these projections. Unlike the norm topology defined by a single norm in normed vector spaces, the product topology handles infinite-dimensional constructions by coordinate-wise convergence and does not rely on metric or norm structures.
Construction of Norm Topology
The construction of norm topology on a vector space is based on defining a norm function that assigns a non-negative length to each vector, inducing a metric through the distance defined by the norm's absolute difference. In contrast, the product topology on a product of normed spaces arises from the Cartesian product of each space with their respective topologies, relying on open sets derived from the component spaces without a direct norm structure. Norm topology provides a finer, metrizable topology that reflects the vector space's geometric structure, while product topology is more general and often coarser, defined purely by coordinate-wise open sets.
Examples Illustrating Each Topology
The product topology on \(\mathbb{R}^2\) is generated by the basis of open rectangles \(U \times V\), where \(U\) and \(V\) are open intervals in \(\mathbb{R}\), illustrating how each coordinate's topology contributes to the overall space. The norm topology on \(\mathbb{R}^2\), defined by the Euclidean norm \(\|(x,y)\| = \sqrt{x^2 + y^2}\), uses open balls as basis elements, reflecting the geometric distance in the plane. Both topologies coincide for finite products of metric spaces, but the product topology extends naturally to infinite products, where the norm topology does not apply.
Comparison of Convergence in Both Topologies
In product topology, a sequence converges if and only if it converges coordinate-wise, meaning convergence occurs independently in each factor space. In contrast, norm topology convergence requires the norm of the difference between sequence elements and the limit to approach zero, implying a stronger, uniform type of convergence. Therefore, convergence in norm topology implies convergence in product topology, but the converse is not generally true, highlighting norm topology's stricter criteria for sequence convergence.
Applications in Analysis and Functional Spaces
Product topology enables the study of infinite-dimensional spaces by equipping Cartesian products of topological spaces with the coarsest topology making all projections continuous, essential in functional analysis for examining convergence and continuity in function spaces. Norm topology, defined by a norm-induced metric, provides a stronger, more intuitive framework for analyzing Banach and Hilbert spaces, facilitating techniques like fixed-point theorems and stability analysis in partial differential equations. Applications in functional spaces often leverage product topology for weak and pointwise convergence, while norm topology underpins strong convergence and operator norm continuity, crucial in optimizing solution properties within applied analysis contexts.
Choosing Between Product and Norm Topologies
Choosing between product and norm topologies depends on the context of convergence and continuity in infinite-dimensional spaces. Product topology, defined by coordinate-wise convergence, is weaker and useful for studying pointwise limits without requiring norm convergence. Norm topology is stronger, inducing uniform convergence and completeness, making it preferable when working with Banach spaces or analyzing stability under perturbations.
Product topology Infographic
 libterm.com
libterm.com