Group algebra combines elements of group theory and algebra by associating a vector space with a group, allowing group operations to be expressed algebraically. This structure plays a crucial role in representation theory, enabling the study of group actions through linear transformations. Explore this article to deepen your understanding of how group algebra shapes modern mathematics and its applications.
Table of Comparison
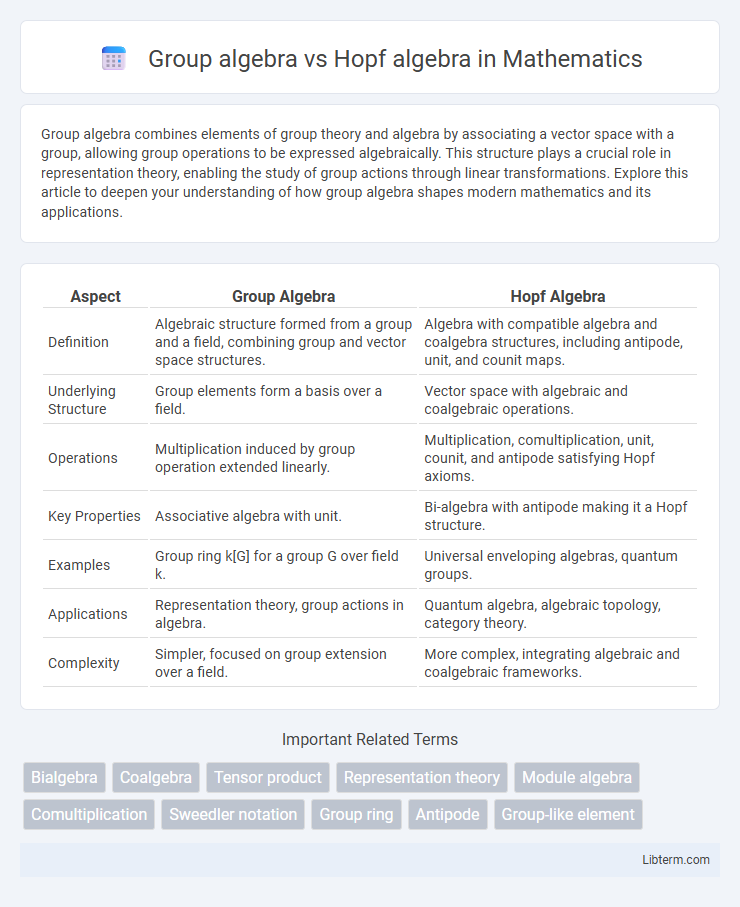
| Aspect | Group Algebra | Hopf Algebra |
|---|---|---|
| Definition | Algebraic structure formed from a group and a field, combining group and vector space structures. | Algebra with compatible algebra and coalgebra structures, including antipode, unit, and counit maps. |
| Underlying Structure | Group elements form a basis over a field. | Vector space with algebraic and coalgebraic operations. |
| Operations | Multiplication induced by group operation extended linearly. | Multiplication, comultiplication, unit, counit, and antipode satisfying Hopf axioms. |
| Key Properties | Associative algebra with unit. | Bi-algebra with antipode making it a Hopf structure. |
| Examples | Group ring k[G] for a group G over field k. | Universal enveloping algebras, quantum groups. |
| Applications | Representation theory, group actions in algebra. | Quantum algebra, algebraic topology, category theory. |
| Complexity | Simpler, focused on group extension over a field. | More complex, integrating algebraic and coalgebraic frameworks. |
Introduction to Group Algebras and Hopf Algebras
Group algebras combine group theory and ring theory by constructing an algebra from a group G and a field K, where elements are formal linear combinations of group elements with coefficients in K, enabling algebraic operations reflecting group structure. Hopf algebras extend this framework by incorporating additional maps--comultiplication, counit, and antipode--that generalize group symmetries to a coalgebra setting, facilitating duality and symmetry operations in quantum groups and algebraic topology. The key distinction lies in Hopf algebras' richer structure allowing the encoding of both algebraic and coalgebraic properties, essential for studying symmetrical objects in noncommutative geometry and theoretical physics.
Fundamental Definitions and Structures
Group algebra is an associative algebra constructed from a group G over a field K, where elements are formal linear combinations of group elements, enabling algebraic manipulation using group operations and scalar multiplication. Hopf algebra extends this structure by incorporating a coproduct, counit, and antipode maps, facilitating dualities and tensor product decompositions, crucial for studying symmetry in algebraic topology and quantum groups. Fundamental definitions involve group algebra being a vector space with basis G, while Hopf algebra is a bialgebra equipped with an antipode that generalizes group inversion in an algebraic framework.
Historical Development and Motivations
Group algebra originated in the early 20th century as a tool to study group representations by associating groups with algebraic structures over fields, facilitating linearization of group theory problems. Hopf algebra emerged mid-20th century from algebraic topology and quantum group theory, extending group algebra concepts to include coproduct, counit, and antipode operations, enabling dualities and symmetry analysis in noncommutative settings. Motivations for group algebras centered on simplifying the study of group actions and symmetries, while Hopf algebras aimed to generalize these ideas and address challenges in topological invariants and quantum symmetries.
Algebraic Properties and Comparisons
Group algebras are associative algebras formed by a group acting as a basis over a field, encapsulating group operations linearly, while Hopf algebras extend this structure by incorporating coalgebra elements such as comultiplication, counit, and antipode, enabling duality and symmetry in algebraic frameworks. The algebraic properties of group algebras emphasize representation theory and module decomposition linked to the underlying group's structure, whereas Hopf algebras support richer interactions through their bialgebra and antipode maps, crucial for quantum group theory and noncommutative geometry. Comparatively, group algebras serve as foundational examples of Hopf algebras with trivial coalgebra structures, whereas the generalized Hopf algebra demands compatibility between algebra and coalgebra structures, reflecting deeper categorical and topological complexities.
Representation Theory: Group vs. Hopf Algebras
Representation theory of group algebras centers on representing group elements as linear transformations on vector spaces, capturing group symmetries through modules over group algebras. Hopf algebras generalize group algebras by incorporating coalgebra structures and antipodes, enabling the study of quantum groups and non-commutative symmetries in representations. This broader framework allows Hopf algebra representations to handle tensor products naturally and leads to applications in quantum field theory and noncommutative geometry.
Coalgebra Structures and Duality
Group algebras are associative algebras formed by linearizing groups, inherently carrying a coalgebra structure via the comultiplication defined by D(g) = g g for group elements g, enabling them to serve as Hopf algebras when combined with an antipode and counit. Hopf algebras generalize group algebras by incorporating a richer coalgebra structure with comultiplication, counit, and antipode maps satisfying compatibility conditions, allowing the study of duality between algebraic and coalgebraic aspects. The duality in Hopf algebras is crucial, as the dual space of a finite-dimensional Hopf algebra also forms a Hopf algebra, facilitating dual coalgebra structures and bridging the representation theories of groups and quantum groups.
Applications in Mathematics and Physics
Group algebras form the foundational framework for studying group representations and symmetries in algebraic structures, crucial in characterizing finite groups and their modules. Hopf algebras extend group algebras by incorporating co-algebraic structures with antipodes, enabling the analysis of quantum groups and non-commutative geometry. In physics, Hopf algebras model symmetries in quantum field theory and integrable systems, while group algebras underpin classical symmetry groups in crystallography and particle physics.
Key Examples: Group Algebra of Finite Groups vs. Classic Hopf Algebras
The group algebra of a finite group G over a field K is a key example that forms an associative algebra with a basis corresponding to elements of G, embedding group structure into algebraic operations. Classic Hopf algebras, such as the universal enveloping algebra of a Lie algebra or the coordinate ring of an algebraic group, incorporate additional structures including coproduct, counit, and antipode, enabling duality and symmetry properties. While the group algebra serves as a foundational construction linking groups and algebras, Hopf algebras generalize this framework to integrate both algebra and coalgebra structures essential for applications in quantum groups and algebraic topology.
Homological and Categorical Perspectives
Group algebras encode groups linearly over fields, enabling homological tools like group cohomology to study their module categories, while Hopf algebras, endowed with compatible algebra and coalgebra structures, generalize group symmetries and allow for richer categorical structures such as monoidal and braided tensor categories. Homological perspectives on Hopf algebras involve Ext and Tor groups within their comodule and module categories, crucial for understanding quantum groups and deformation theory. Categorical approaches emphasize that Hopf algebras naturally live in braided monoidal categories, enabling constructions like Drinfeld doubles, whereas group algebras correspond to simpler symmetric monoidal categories reflecting classical group representations.
Open Problems and Future Directions
Group algebras, which provide a linearized framework for studying group representations, face open problems in characterizing their module categories and understanding extensions in non-semisimple cases. Hopf algebras, generalizing group algebras with additional coalgebra and antipode structures, confront challenges in classifying finite-dimensional Hopf algebras and exploring their applications in quantum symmetries and noncommutative geometry. Future directions include developing deeper insights into the representation theory of infinite-dimensional Hopf algebras and constructing new algebraic invariants that bridge the theories of group and Hopf algebras.
Group algebra Infographic
 libterm.com
libterm.com