A free module offers users access to valuable features without any cost, making it an excellent choice for those seeking budget-friendly solutions. Its seamless integration and user-friendly interface ensure you can maximize productivity effortlessly. Discover how this free module can transform your experience by reading the full article.
Table of Comparison
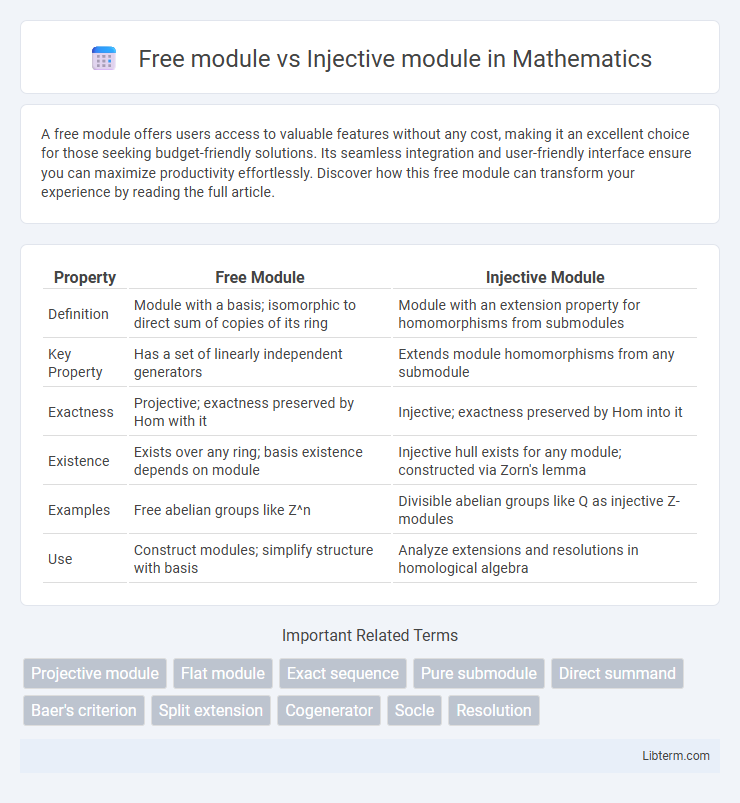
| Property | Free Module | Injective Module |
|---|---|---|
| Definition | Module with a basis; isomorphic to direct sum of copies of its ring | Module with an extension property for homomorphisms from submodules |
| Key Property | Has a set of linearly independent generators | Extends module homomorphisms from any submodule |
| Exactness | Projective; exactness preserved by Hom with it | Injective; exactness preserved by Hom into it |
| Existence | Exists over any ring; basis existence depends on module | Injective hull exists for any module; constructed via Zorn's lemma |
| Examples | Free abelian groups like Z^n | Divisible abelian groups like Q as injective Z-modules |
| Use | Construct modules; simplify structure with basis | Analyze extensions and resolutions in homological algebra |
Introduction to Modules in Algebra
Free modules are algebraic structures that possess a basis, allowing every element to be uniquely expressed as a linear combination of basis elements over a ring, making them analogous to vector spaces with bases. Injective modules, in contrast, are defined by their extension property where any homomorphism from a submodule can be extended to the entire module, serving as a categorical analogue to divisible groups in module theory. The distinction between free and injective modules highlights fundamental concepts in module theory, emphasizing basis representation versus extension properties within algebraic structures over rings.
Defining Free Modules
Free modules are modules that possess a basis, meaning every element can be uniquely expressed as a finite linear combination of basis elements with coefficients from the ring. They generalize the concept of vector spaces to modules over arbitrary rings, where the basis provides a straightforward structure facilitating module homomorphisms. In contrast, injective modules are characterized by the extension property for homomorphisms, serving a dual role in module theory not defined by the existence of a basis.
Understanding Injective Modules
Injective modules are characterized by their property that any homomorphism defined on a submodule can be extended to the whole module, making them essential in homological algebra and module theory. Unlike free modules, which have bases allowing for straightforward decompositions, injective modules often serve as injective hulls, providing minimal injective extensions crucial for resolving exact sequences. The Baer Criterion offers a practical test for injectivity, stating that a module is injective if every homomorphism from an ideal can be extended to the entire ring, emphasizing their role in ring and module homomorphisms.
Key Properties of Free Modules
Free modules are characterized by having a basis, which allows every element to be uniquely expressed as a linear combination of basis elements, ensuring projectivity and flatness. They possess a universal property that any module homomorphism from the basis set extends uniquely to the entire free module. Unlike injective modules, which are defined by their extension property for homomorphisms into them, free modules provide a constructive framework for module generation and direct sum decompositions.
Essential Characteristics of Injective Modules
Injective modules are defined by their essential property of being direct summands of every module containing them as submodules, ensuring any homomorphism from a submodule extends to the entire module. Unlike free modules, which have bases and exhibit projective characteristics, injective modules are characterized by their ability to absorb homomorphic images through extension, reflecting their role in the Baer criterion for injectivity. This essential extensibility property distinguishes injective modules in module theory, facilitating exactness in Hom functors and making them crucial in homological algebra.
Structural Differences Between Free and Injective Modules
Free modules are characterized by having a basis, allowing every element to be uniquely expressed as a finite linear combination of basis elements, which provides a direct sum decomposition aligned with the underlying ring. Injective modules possess the extension property, enabling any homomorphism defined on a submodule to extend over the entire module, reflecting their role as "large" or "complete" modules within the category. Structurally, free modules exhibit a rigid, well-defined generator set facilitating constructive decompositions, while injective modules display a maximal and flexible structure essential for embedding and homological considerations in module theory.
Examples Illustrating Free versus Injective Modules
Free modules over a ring R are characterized by having a basis, such as R^n, the direct sum of n copies of R, which allows every element to be expressed uniquely as an R-linear combination of basis elements. In contrast, injective modules, like the injective hull of an R-module or the rational numbers \(\mathbb{Q}\) as an injective \(\mathbb{Z}\)-module, serve as extension-friendly modules allowing homomorphisms to extend from submodules. While free modules demonstrate explicit structural generation, injective modules are fundamentally important in homological algebra for their role in exact sequence splitting and injective resolutions.
Applications of Free and Injective Modules
Free modules play a crucial role in algebraic topology and homological algebra by providing a basis that simplifies computations in chain complexes and module decompositions. Injective modules are essential in homological algebra and category theory for constructing injective resolutions, facilitating Ext and derived functor calculations. Both modules support algebraic structures in module theory, with free modules enabling explicit generator descriptions, while injective modules ensure exactness and extension properties in module homomorphisms.
When to Use Free Modules vs Injective Modules
Free modules are ideal when constructing explicit bases for modules or when working with modules over principal ideal domains, as they provide a clear structure with elements that generate the module freely. Injective modules are preferred in homological algebra for extending homomorphisms and resolving exact sequences, especially useful in defining injective resolutions and computing derived functors like Ext. Choosing free modules benefits explicit calculations and structural clarity, while injective modules facilitate theoretical analysis of module extensions and cohomological properties.
Conclusion: Choosing Between Free and Injective Modules
Free modules provide a concrete and constructive framework ideal for computations and explicit basis representation, making them essential in linear algebra and module theory. Injective modules, characterized by their extension properties and ability to absorb embeddings, are crucial in homological algebra and resolving exact sequences. The choice between free and injective modules depends on the context: select free modules for explicit construction and basis manipulation, while favoring injective modules for advanced theoretical applications involving extensions and cohomology.
Free module Infographic
 libterm.com
libterm.com