A quasi-projective variety is an important concept in algebraic geometry, defined as an open subset of a projective variety, combining properties of both affine and projective varieties. It allows for the study of geometric objects that are more flexible than projective varieties alone, enabling a broader range of applications in mathematical research. Explore the article further to deepen your understanding of quasi-projective varieties and their role in complex geometric structures.
Table of Comparison
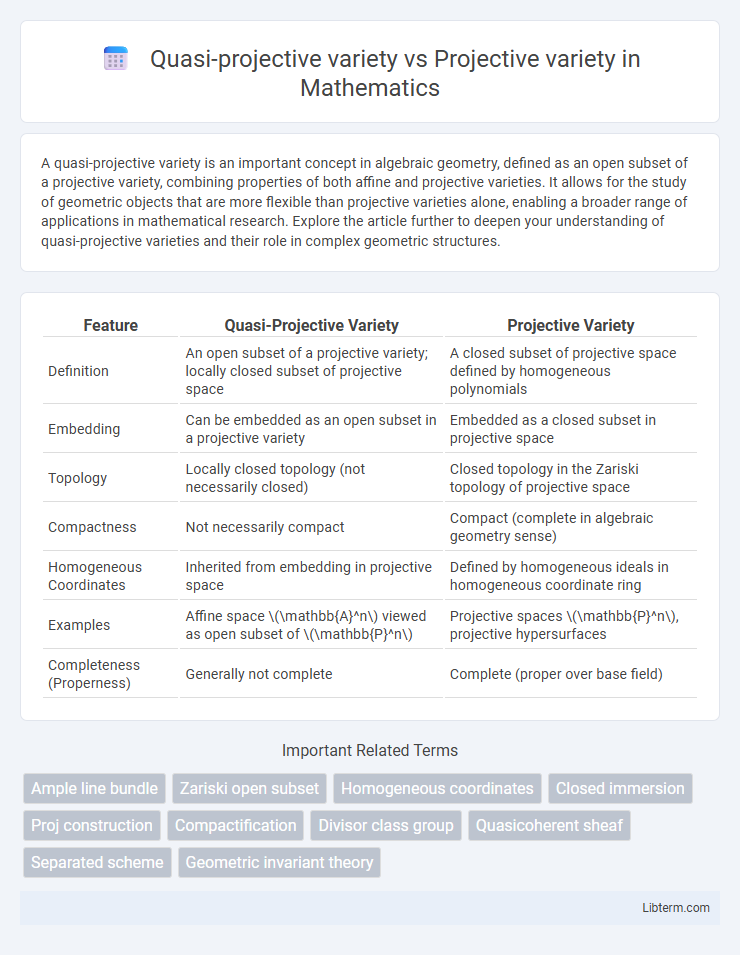
| Feature | Quasi-Projective Variety | Projective Variety |
|---|---|---|
| Definition | An open subset of a projective variety; locally closed subset of projective space | A closed subset of projective space defined by homogeneous polynomials |
| Embedding | Can be embedded as an open subset in a projective variety | Embedded as a closed subset in projective space |
| Topology | Locally closed topology (not necessarily closed) | Closed topology in the Zariski topology of projective space |
| Compactness | Not necessarily compact | Compact (complete in algebraic geometry sense) |
| Homogeneous Coordinates | Inherited from embedding in projective space | Defined by homogeneous ideals in homogeneous coordinate ring |
| Examples | Affine space \(\mathbb{A}^n\) viewed as open subset of \(\mathbb{P}^n\) | Projective spaces \(\mathbb{P}^n\), projective hypersurfaces |
| Completeness (Properness) | Generally not complete | Complete (proper over base field) |
Introduction to Projective and Quasi-projective Varieties
Projective varieties are defined as the zero sets of homogeneous polynomials in projective space, characterized by their compactness and embedding into projective space \( \mathbb{P}^n \). Quasi-projective varieties arise as open subsets of projective varieties, allowing more flexible geometric structures by excluding certain closed subsets. Understanding the relationship between projective and quasi-projective varieties is fundamental in algebraic geometry, as it connects the global properties of projective varieties with the local and affine-like nature of quasi-projective varieties.
Definitions: Projective Variety Explained
A projective variety is defined as the zero set of a collection of homogeneous polynomials in a projective space \(\mathbb{P}^n\), characterized by being a closed subset with respect to the Zariski topology. In contrast, a quasi-projective variety is an open subset of a projective variety, obtained by removing a closed subvariety, thus it inherits a locally closed structure in \(\mathbb{P}^n\). Projective varieties possess compactness properties within algebraic geometry, while quasi-projective varieties generalize this concept by allowing the exclusion of certain closed subsets, facilitating the study of more flexible geometric objects.
Understanding Quasi-projective Varieties
Quasi-projective varieties are subsets of projective varieties obtained by removing a closed subset, making them open subvarieties within a projective variety that inherit many geometric properties but allow more flexibility in structure. Unlike projective varieties, which are complete and compact in the Zariski topology, quasi-projective varieties are not necessarily complete, enabling richer local analysis and embedding into projective space minus some constraints. Understanding quasi-projective varieties involves studying their open embedding into projective varieties, their role in moduli problems, and their connection to affine varieties through localization techniques.
Key Differences Between Projective and Quasi-projective Varieties
Projective varieties are defined as the zero sets of homogeneous polynomials in projective space, making them complete and compact algebraic varieties, while quasi-projective varieties are open subsets of projective varieties, hence they can lack compactness and completeness. Projective varieties possess a fixed embedding into projective space, reflecting their global geometric properties, whereas quasi-projective varieties allow more flexible embeddings as locally closed subsets, combining features of both affine and projective varieties. The distinction impacts their geometric behavior, with projective varieties often exhibiting stronger cohomological properties and quasi-projective varieties providing a broader setting for studying open or non-compact algebraic structures.
Construction Methods for Projective Varieties
Projective varieties are constructed as zero loci of homogeneous polynomials in projective space, utilizing the tools of homogeneous coordinate rings and graded ideals to define geometric objects up to scalar multiplication. Quasi-projective varieties arise as open subsets of projective varieties, formed by removing closed subvarieties specified by additional equations or conditions, retaining a locally projective structure but allowing more flexibility. The primary construction method for projective varieties leverages the Proj construction of graded rings, which systematically associates abstract projective schemes with homogeneous coordinate data.
How Quasi-projective Varieties are Formed
Quasi-projective varieties are formed by taking open subsets of projective varieties, specifically by removing a closed subvariety from a projective variety. This construction allows quasi-projective varieties to inherit many geometric properties from projective varieties while providing greater flexibility in their structure. Unlike projective varieties that are compact and complete, quasi-projective varieties are typically non-compact due to the exclusion of closed subsets.
Morphisms and Maps: Comparative Analysis
Quasi-projective varieties are open subsets of projective varieties and admit embeddings into projective space, enabling morphisms that extend to projective maps with restrictions. Projective varieties, being complete and closed in projective space, ensure all regular maps between them are proper morphisms, facilitating well-defined pushforwards and pullbacks in cohomology. Morphisms from quasi-projective varieties to projective varieties may fail to be proper, impacting the compactness properties crucial for geometric and categorical equivalences in algebraic geometry.
Geometric Properties: Compactness and Completeness
Projective varieties are algebraic varieties embedded in projective space and are inherently compact and complete, meaning every morphism from a projective variety to another variety is proper. Quasi-projective varieties arise as open subsets of projective varieties, inheriting many geometric properties but lacking compactness and completeness due to the removal of a closed subset. This distinction in geometric properties influences key algebraic and topological behaviors, such as the extension of morphisms and the finiteness of cohomology groups.
Applications in Algebraic Geometry
Quasi-projective varieties serve as fundamental objects in algebraic geometry due to their flexibility in embedding affine and projective features, making them essential for studying morphisms and intersection theory. Projective varieties, characterized by their compactness and homogeneous coordinate ring structure, underpin classical results in enumerative geometry and moduli space construction. Both types are crucial for the classification of algebraic varieties, with projective varieties enabling the use of ample line bundles and quasi-projective varieties facilitating open subset analysis in geometric modeling.
Summary: Choosing Between Quasi-projective and Projective Varieties
Quasi-projective varieties are open subsets of projective varieties, allowing more flexibility in geometric constructions while still embedding into projective space. Projective varieties are closed subsets in projective space, providing compactness and enabling the use of tools like projective duality and intersection theory. The choice depends on the desired properties: projective varieties ensure completeness and facilitate global geometric arguments, whereas quasi-projective varieties allow studying local or affine-like behaviors within a projective framework.
Quasi-projective variety Infographic
 libterm.com
libterm.com