A finite set is a collection of distinct elements with a specific number of members that can be counted. This concept is fundamental in mathematics, as it contrasts with infinite sets, which have unlimited elements. Explore the rest of the article to understand how finite sets are applied in various fields and their mathematical properties.
Table of Comparison
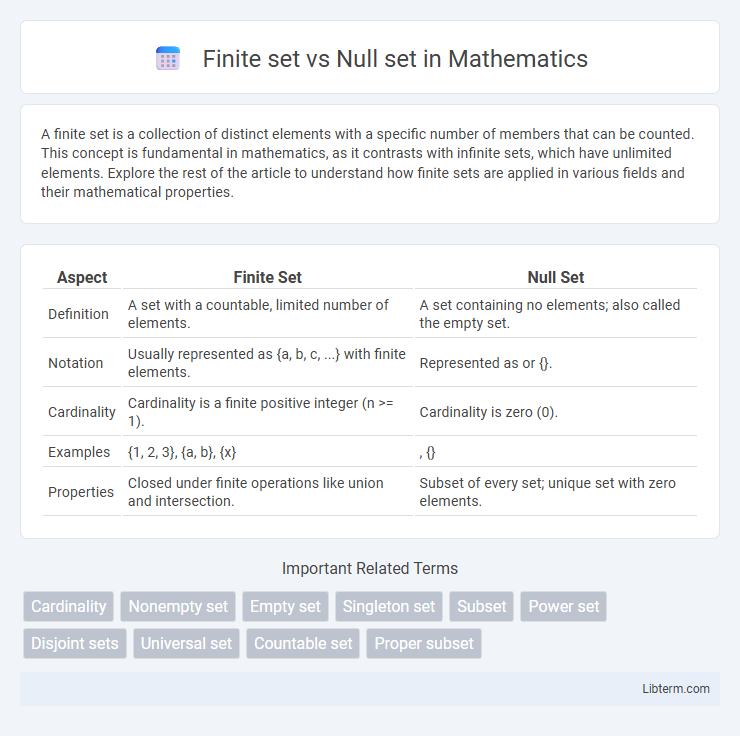
| Aspect | Finite Set | Null Set |
|---|---|---|
| Definition | A set with a countable, limited number of elements. | A set containing no elements; also called the empty set. |
| Notation | Usually represented as {a, b, c, ...} with finite elements. | Represented as or {}. |
| Cardinality | Cardinality is a finite positive integer (n >= 1). | Cardinality is zero (0). |
| Examples | {1, 2, 3}, {a, b}, {x} | , {} |
| Properties | Closed under finite operations like union and intersection. | Subset of every set; unique set with zero elements. |
Introduction to Sets in Mathematics
A finite set in mathematics contains a specific number of distinct elements, allowing precise counting and comparison, whereas a null set, also known as the empty set, contains no elements at all, symbolized by O or {}. Finite sets are fundamental in understanding concepts like cardinality and subsets, while the null set serves as the unique subset of every set and a key element in set theory axioms. The contrast between finite and null sets highlights the foundational role of element presence and quantity in set analysis.
Defining the Finite Set
A finite set is a collection of distinct elements with a countable number of members, meaning its elements can be paired one-to-one with a set of natural numbers from 1 to n, where n is a non-negative integer. Unlike a null set, which contains no elements, a finite set has a clearly defined size or cardinality greater than zero. Understanding the finite set's definition is crucial for distinguishing it from infinite and null sets in set theory and discrete mathematics.
Understanding the Null Set (Empty Set)
The null set, also known as the empty set, contains no elements and is denoted by {} or , representing the unique set with zero members. It is a finite set because its cardinality, or size, is zero, distinguishing it from other finite sets that contain one or more elements. In set theory, the null set serves as the foundational element for building all other sets and plays a crucial role in defining concepts like subsets and intersections.
Key Differences: Finite Set vs Null Set
A finite set contains a specific number of distinct elements, such as {1, 2, 3}, with a defined cardinality greater than zero. A null set, or empty set, contains no elements and is represented by , having a cardinality of zero. The key difference lies in their element count: finite sets have measurable, positive size while null sets have none.
Symbolic Representation of Finite and Null Sets
Finite sets are symbolized by curly braces containing a limited number of distinct elements, such as \( A = \{1, 2, 3\} \), indicating that the set contains exactly three elements. Null sets, also called empty sets, are denoted by the symbol \( \emptyset \) or \( \{\} \), signifying the absence of any elements within the set. This symbolic representation clearly distinguishes finite sets from null sets in mathematical notation.
Cardinality: Counting Elements in Sets
Finite sets have a specific cardinality represented by a non-negative integer that counts the exact number of elements within the set. Null sets, also called empty sets, have a cardinality of zero, indicating the absence of any elements. Understanding cardinality helps in differentiating finite sets with elements from null sets that contain none.
Examples of Finite Sets
A finite set contains a specific number of elements, such as the set {2, 4, 6, 8} representing even numbers less than 10, or the set {Monday, Tuesday, Wednesday} indicating days of the week. Each element in a finite set is countable, allowing precise enumeration and clear identification. In contrast, a null set, denoted by {}, contains no elements at all, exemplifying an empty collection.
Examples of Null Sets
Null sets, also known as empty sets, contain no elements, making them distinct from finite sets which have a specific number of elements. Examples of null sets include the set of natural numbers less than zero and the set of real solutions to the equation x2 + 1 = 0 within the real number system. These examples illustrate that null sets are characterized by the complete absence of members, unlike finite sets which possess a countable quantity of elements.
Applications of Finite and Null Sets
Finite sets are crucial in computer science for algorithm analysis, database management, and coding theory, where a clearly countable number of elements must be processed efficiently. Null sets, representing empty collections, play a vital role in mathematical proofs, logic, and probability theory by defining base cases and scenarios with zero occurrence or invalid states. Both finite and null sets underpin the foundation of discrete mathematics, enabling precise modeling and problem solving in engineering, statistics, and data science.
Summary: Finite Set vs Null Set
A finite set contains a specific number of elements that can be counted and listed one by one, such as {1, 2, 3}, whereas a null set, also known as an empty set, contains no elements at all, represented as {} or . Finite sets have a cardinality greater than zero, while the null set has a cardinality of zero. Understanding the distinction between finite and null sets is fundamental in set theory, influencing concepts in mathematics, computer science, and logic.
Finite set Infographic
 libterm.com
libterm.com