The Witt group is a fundamental structure in algebra and quadratic form theory, classifying equivalence classes of quadratic spaces over a field. Its properties reveal deep interactions between algebraic forms and number theory, making it essential in advanced mathematical research and applications. Explore this article to understand how the Witt group can provide insights into your study of algebraic systems.
Table of Comparison
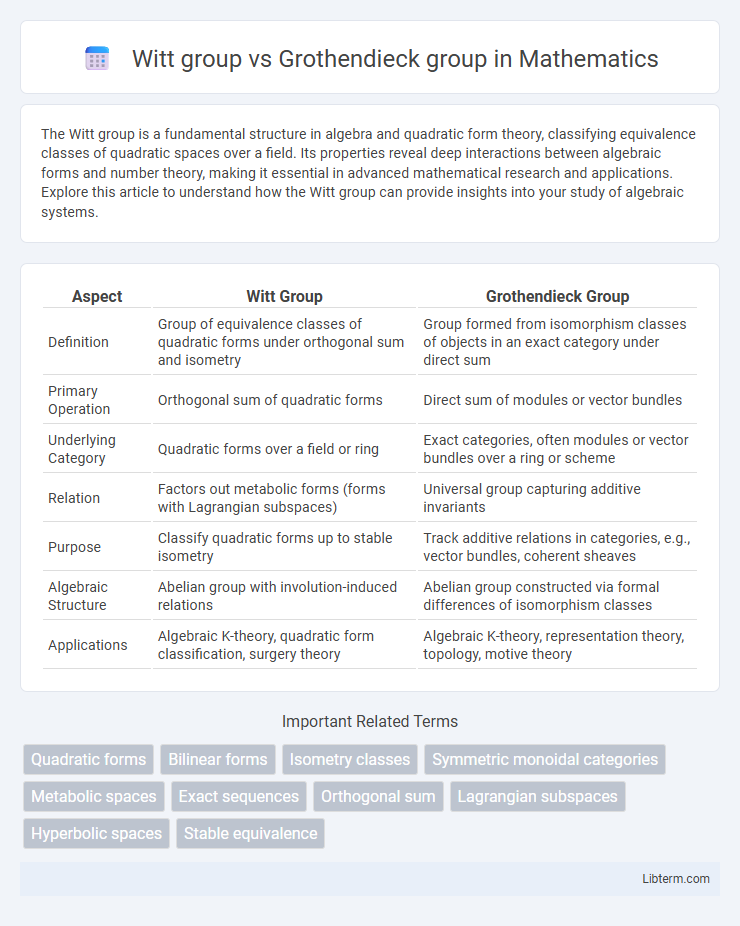
| Aspect | Witt Group | Grothendieck Group |
|---|---|---|
| Definition | Group of equivalence classes of quadratic forms under orthogonal sum and isometry | Group formed from isomorphism classes of objects in an exact category under direct sum |
| Primary Operation | Orthogonal sum of quadratic forms | Direct sum of modules or vector bundles |
| Underlying Category | Quadratic forms over a field or ring | Exact categories, often modules or vector bundles over a ring or scheme |
| Relation | Factors out metabolic forms (forms with Lagrangian subspaces) | Universal group capturing additive invariants |
| Purpose | Classify quadratic forms up to stable isometry | Track additive relations in categories, e.g., vector bundles, coherent sheaves |
| Algebraic Structure | Abelian group with involution-induced relations | Abelian group constructed via formal differences of isomorphism classes |
| Applications | Algebraic K-theory, quadratic form classification, surgery theory | Algebraic K-theory, representation theory, topology, motive theory |
Introduction to Witt Group and Grothendieck Group
The Witt group classifies equivalence classes of quadratic forms over a field, capturing intricate algebraic and geometric properties through bilinear form theory. The Grothendieck group, constructed from an exact category or a monoid, formalizes the notion of additive invariants and serves as a universal group completion reflecting isomorphism classes of vector bundles or projective modules. Both groups provide foundational frameworks in algebraic K-theory, with the Witt group focusing on quadratic forms and the Grothendieck group extending to broader categorical contexts.
Historical Background: Witt and Grothendieck
The Witt group, introduced by Ernst Witt in the 1930s, classifies quadratic forms over a field by considering equivalence classes under orthogonal sums and metabolic forms. Grothendieck developed the Grothendieck group concept in the late 1950s to formalize K-theory, capturing the structure of vector bundles and coherent sheaves through stable isomorphism classes and virtual objects. While Witt's work primarily addresses quadratic forms in algebra and number theory, Grothendieck's construction provides a broad framework for additive invariants in algebraic geometry and topology.
Definitions: Witt Group Explained
The Witt group classifies quadratic forms over a field by identifying forms that differ by hyperbolic planes, emphasizing equivalence under metabolic forms. In contrast, the Grothendieck group arises from isomorphism classes of vector bundles or modules, focusing on direct sum operations without quadratic form structures. Witt groups capture refined algebraic invariants linked to quadratic form equivalences, while Grothendieck groups provide a broader framework for additive equivalence classes.
Grothendieck Group: Core Concepts
The Grothendieck group is constructed from a commutative monoid by formally adding inverses, enabling an abelian group structure that captures equivalence classes of objects such as vector bundles or projective modules. Central to algebraic K-theory, the Grothendieck group K0 encodes exact sequences and additive invariants, reflecting the categorical framework of decompositions and extensions. This group differs from the Witt group, which classifies quadratic forms up to stable isomorphism and metabolic reduction, focusing specifically on symmetric bilinear or quadratic structure rather than additive classes.
Algebraic Structures: Key Differences
The Witt group classifies quadratic forms over a field, capturing equivalence classes under orthogonal sum and hyperbolic forms, while the Grothendieck group generalizes additive invariants from exact categories by completing monoids to groups via formal differences. In algebraic structures, the Witt group emphasizes the algebraic theory of quadratic forms and their isotropy, contrasting with the Grothendieck group's broader role in K-theory and categorification involving vector bundles or modules. These distinctions highlight the Witt group's specialization in bilinear forms versus the Grothendieck group's foundational construction governing additive invariants in homological algebra.
Applications in Algebraic Geometry
The Witt group classifies quadratic forms over a field and plays a crucial role in studying bilinear forms and their equivalence classes in algebraic geometry. The Grothendieck group, defined from exact categories or coherent sheaves, captures vector bundles and coherent sheaf classes, enabling computations in K-theory and intersection theory. Applications in algebraic geometry often use the Witt group to analyze quadratic bundles and the Grothendieck group for understanding vector bundle decompositions and characteristic classes on algebraic varieties.
Witt Group vs Grothendieck Group: Comparative Analysis
The Witt group classifies quadratic forms over a field up to stable isometry, capturing finer equivalence relations by considering metabolic forms, while the Grothendieck group arises from isomorphism classes of objects in an exact category under direct sum operations. Witt groups incorporate bilinear or quadratic form structures with equivalence generated by hyperbolic forms, contrasting with Grothendieck groups which primarily handle additive invariants without bilinear form data. Comparative analysis reveals that Witt groups refine Grothendieck groups by encoding quadratic form information and equivalences beyond those tracked by mere direct sum decompositions.
Notable Examples and Constructions
The Witt group classifies quadratic forms over a field up to stable isomorphism, with prominent examples including the Witt ring of real numbers where the signature map plays a crucial role. The Grothendieck group arises from forming the group completion of a commutative monoid, such as the category of vector bundles over a topological space, producing K-theory groups essential in algebraic topology and geometry. Notable constructions include the Witt group as a quotient of the Grothendieck group of quadratic spaces by metabolic forms, linking these concepts through exact sequences in derived categories.
Recent Research and Developments
Recent research on Witt groups vs Grothendieck groups highlights advances in algebraic K-theory and quadratic form classification, emphasizing their distinct yet interconnected roles in topology and algebraic geometry. Studies have explored refined invariants in Witt groups, particularly in relation to derived categories and motivic cohomology, enhancing understanding of bilinear forms over rings and schemes. Developments in computational techniques and categorical frameworks continue to expand applications in arithmetic geometry and modular representation theory.
Conclusion: Significance and Future Directions
The Witt group captures quadratic form classifications with an emphasis on forms modulo metabolic ones, offering refined invariants beyond the additive structure of the Grothendieck group, which classifies vector bundles or modules via stable isomorphism classes. This distinction enables deeper insights into algebraic and topological structures, particularly in quadratic and hermitian categories, with ongoing research exploring applications in algebraic K-theory, motivic homotopy theory, and their connections to arithmetic geometry. Future directions involve extending Witt group frameworks to derived and equivariant settings, enhancing computational methods, and uncovering novel interactions with cohomological invariants to further elucidate structural and classification problems.
Witt group Infographic
 libterm.com
libterm.com