A linear manifold is a subset of a vector space that can be expressed as a translation of a linear subspace by a fixed vector, preserving the structure of linearity in a shifted form. This concept is essential in linear algebra and functional analysis, as it generalizes the notion of a subspace while enabling the study of affine sets and solution spaces to linear equations. Explore the rest of the article to deepen your understanding of linear manifolds and their applications in various mathematical contexts.
Table of Comparison
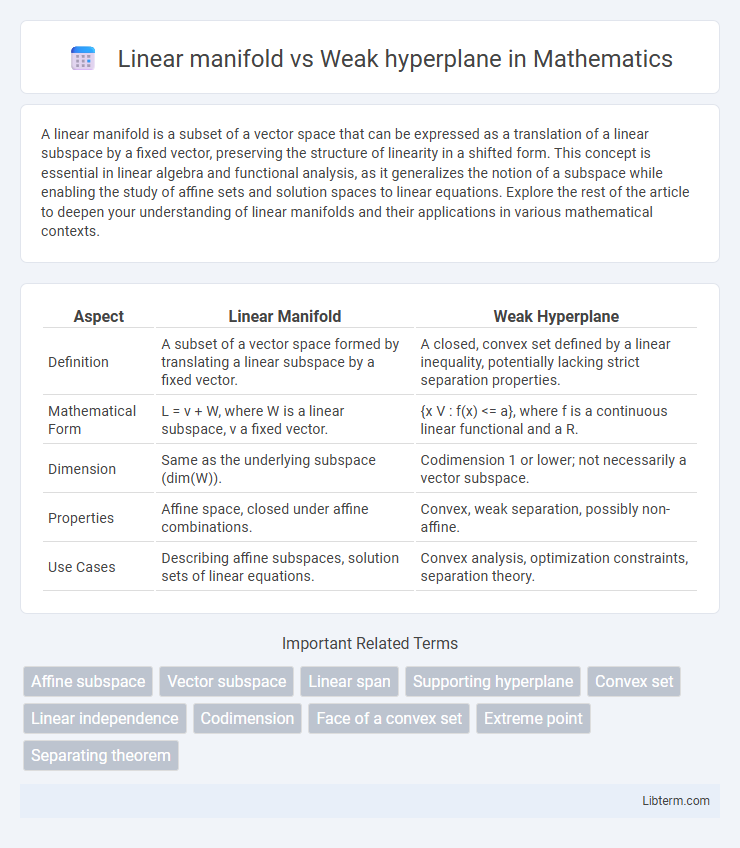
| Aspect | Linear Manifold | Weak Hyperplane |
|---|---|---|
| Definition | A subset of a vector space formed by translating a linear subspace by a fixed vector. | A closed, convex set defined by a linear inequality, potentially lacking strict separation properties. |
| Mathematical Form | L = v + W, where W is a linear subspace, v a fixed vector. | {x V : f(x) <= a}, where f is a continuous linear functional and a R. |
| Dimension | Same as the underlying subspace (dim(W)). | Codimension 1 or lower; not necessarily a vector subspace. |
| Properties | Affine space, closed under affine combinations. | Convex, weak separation, possibly non-affine. |
| Use Cases | Describing affine subspaces, solution sets of linear equations. | Convex analysis, optimization constraints, separation theory. |
Introduction to Linear Manifolds and Weak Hyperplanes
Linear manifolds are geometric structures representing affine subspaces in vector spaces, characterized by translation of linear subspaces by a fixed vector, enabling solutions to systems of linear equations. Weak hyperplanes generalize traditional hyperplanes by relaxing separation conditions, allowing for partial containment of points and broader applications in functional analysis and optimization theory. Understanding the distinction illuminates how linear manifolds provide exact affine representations, while weak hyperplanes accommodate approximate or weaker constraints in high-dimensional spaces.
Defining Linear Manifolds: Concepts and Properties
A linear manifold in a vector space is a translation of a linear subspace by a fixed vector, retaining the structure of an affine set without necessarily passing through the origin. It can be expressed as \( M = v + W \), where \( v \) is a fixed vector and \( W \) is a linear subspace, highlighting its role as an affine subset. Unlike weak hyperplanes, which are particular cases of linear manifolds with codimension one, linear manifolds encompass a broader category characterized by their dimension and affine properties.
What is a Weak Hyperplane? Key Characteristics
A weak hyperplane is a subspace in a vector space that may not be fully affine or linear but still separates points within a certain margin, making it crucial in optimization and machine learning contexts, particularly in support vector machines (SVMs). Unlike a linear manifold, which is a flat, affine subspace characterized by strict linearity and closure under vector addition and scalar multiplication, a weak hyperplane allows for a more flexible boundary that tolerates some margin of error or slack. Key characteristics of a weak hyperplane include its reliance on inequality constraints, the presence of margin violations, and its role in maximizing the separation margin between data classes while permitting some flexibility for non-linearly separable data.
Dimensionality: Linear Manifold vs Weak Hyperplane
Linear manifolds generalize linear subspaces by allowing affine shifts, maintaining a dimension equal to that of their underlying subspace, which can range from zero up to the ambient space dimension. Weak hyperplanes, often defined as subsets of codimension one, have a dimension exactly one less than the ambient space, representing critical boundaries in high-dimensional geometry. This distinction in dimensionality affects their roles in data separation, with linear manifolds enabling flexible affine transformations while weak hyperplanes act as minimal separators or decision boundaries.
Algebraic Structure and Representation
A linear manifold in a vector space is an affine subspace formed by translating a linear subspace, maintaining the algebraic structure of closure under vector addition and scalar multiplication within the subspace. Weak hyperplanes, often defined in infinite-dimensional spaces, lack strict linearity but still represent a codimension-one structure, serving as kernels of functionals that may be discontinuous or not fully bounded. The representation of linear manifolds relies on explicit vector addition and scalar operations, whereas weak hyperplanes are characterized algebraically through continuous or weak* topologies in dual spaces, emphasizing their role in functional analysis and operator theory.
Geometric Interpretation and Visualization
A linear manifold is a flat, affine subspace of a vector space that can be visualized as a translated linear subspace, characterized by parallelism and dimensionality equal to that of the underlying subspace. In contrast, a weak hyperplane is a boundary in a geometric space that may not have full dimensionality or strict linearity, often representing a relaxed constraint or generalized separating surface within vector spaces. Visualization of a linear manifold involves clear flatness and uniform direction, whereas a weak hyperplane appears as a less rigid, possibly curved or incomplete boundary demarcating distinct regions.
Role in Linear Algebra and Vector Spaces
A linear manifold in linear algebra represents a translation of a linear subspace by a fixed vector, forming an affine subset that preserves the vector space structure minus the origin. A weak hyperplane, often characterized as a codimension-one subspace or a nearly separating set, plays a crucial role in understanding boundaries and supports within vector spaces. Both concepts are fundamental in linear algebra, with linear manifolds facilitating affine geometry and weak hyperplanes aiding in the study of convexity and functional separation in vector spaces.
Applications in Data Science and Machine Learning
Linear manifolds are crucial in dimensionality reduction techniques like Principal Component Analysis (PCA), capturing data variance within subspaces for feature extraction and noise reduction. Weak hyperplanes, often utilized in support vector machines (SVMs), enable margin maximization in classification tasks despite data non-separability or noise, improving model robustness. Both concepts facilitate efficient data representation and decision boundaries, enhancing performance in clustering, classification, and regression models within machine learning pipelines.
Comparing Linear Independence and Span
A linear manifold is defined as a translation of a linear subspace, maintaining the properties of linear independence and span within its underlying vector space, whereas a weak hyperplane, often a subset that may not sustain full linear independence, represents a relaxed constraint that does not necessarily span the entire ambient space. Linear independence in a linear manifold guarantees that no vector can be represented as a combination of others, ensuring a well-defined dimension equal to the span of its basis vectors. In contrast, a weak hyperplane may allow dependencies among vectors, resulting in a lower or less strictly defined dimension and a potentially reduced or partial span within the vector space.
Summary: Key Differences and Implications
Linear manifolds are affine subspaces obtained by translating a linear subspace, preserving linearity and dimensionality within vector spaces. Weak hyperplanes are generalized boundaries that may lack strict linearity but serve as critical separators in optimization and geometric analysis. Understanding these distinctions informs applications in machine learning, convex analysis, and signal processing where linear structure versus flexibility affects solution strategies.
Linear manifold Infographic
 libterm.com
libterm.com