Lower bound refers to the smallest possible value or limit that a mathematical function, algorithm, or data set can take or achieve. Understanding lower bounds is crucial in optimization problems, algorithm analysis, and computational complexity to determine minimum performance thresholds. Explore the rest of the article to learn how lower bounds impact your computational and analytical tasks.
Table of Comparison
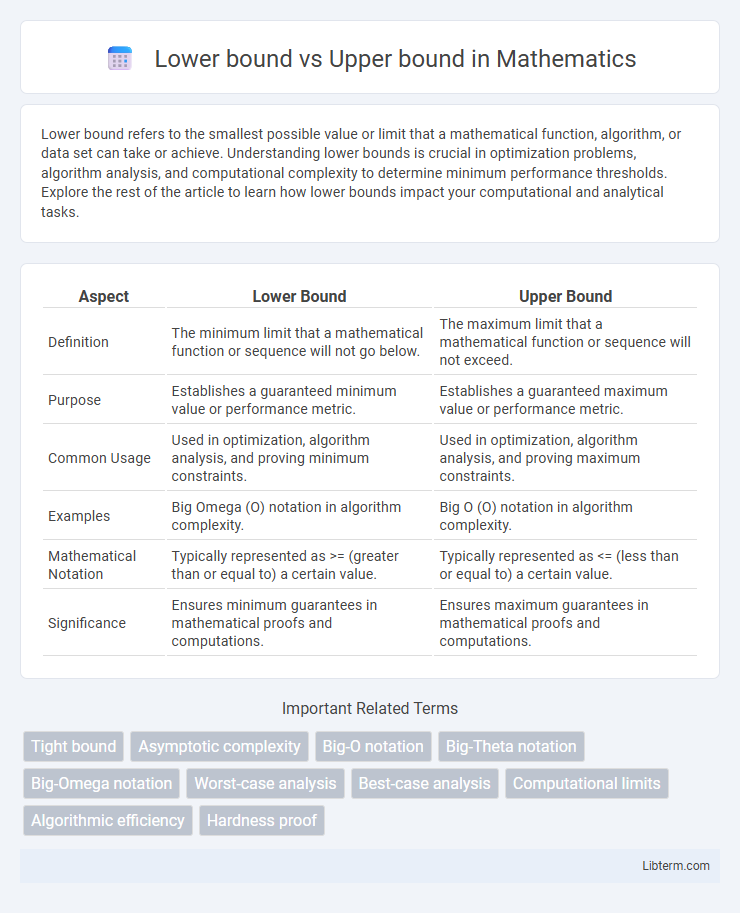
| Aspect | Lower Bound | Upper Bound |
|---|---|---|
| Definition | The minimum limit that a mathematical function or sequence will not go below. | The maximum limit that a mathematical function or sequence will not exceed. |
| Purpose | Establishes a guaranteed minimum value or performance metric. | Establishes a guaranteed maximum value or performance metric. |
| Common Usage | Used in optimization, algorithm analysis, and proving minimum constraints. | Used in optimization, algorithm analysis, and proving maximum constraints. |
| Examples | Big Omega (O) notation in algorithm complexity. | Big O (O) notation in algorithm complexity. |
| Mathematical Notation | Typically represented as >= (greater than or equal to) a certain value. | Typically represented as <= (less than or equal to) a certain value. |
| Significance | Ensures minimum guarantees in mathematical proofs and computations. | Ensures maximum guarantees in mathematical proofs and computations. |
Introduction to Bounds in Mathematics
Lower bound and upper bound are fundamental concepts in mathematics that define the limits within which elements of a set or solutions to problems must lie. A lower bound represents the smallest value that is guaranteed to be less than or equal to every element in the set, while an upper bound is the largest value greater than or equal to every element. These bounds are essential in optimization, analysis, and proving convergence within various mathematical contexts.
Definition of Lower Bound
The lower bound in algorithm analysis defines the minimum limit on the running time or complexity that any algorithm solving a particular problem must have, ensuring no algorithm can perform better than this bound. It establishes a baseline metric for evaluating the efficiency of algorithms within computational complexity theory. Lower bounds are crucial for proving the inherent difficulty of problems, particularly in sorting, searching, and optimization tasks.
Definition of Upper Bound
Upper bound refers to the smallest value or limit that is greater than or equal to every element in a given set or sequence, ensuring no elements exceed this threshold. It is a critical concept in mathematics and computer science for establishing constraints within algorithms and data structures. Defining the upper bound helps optimize performance by limiting the scope of possible values for variables or functions.
Key Differences: Lower Bound vs Upper Bound
Lower bound represents the minimum possible value or limit that a function, algorithm, or dataset can take, ensuring performance or outcomes cannot be better than this threshold. Upper bound indicates the maximum achievable value or limit, defining the worst-case scenario or highest resource consumption expected. Key differences include that lower bound sets a theoretical minimum for complexity or size, while upper bound defines an absolute maximum, both crucial in algorithm analysis and problem-solving constraints.
Importance of Bounds in Problem Solving
Bounds in problem-solving define the limits within which solutions must be found, with lower bounds establishing minimum performance thresholds and upper bounds setting maximum constraints. Identifying tight bounds allows algorithms to be evaluated for efficiency and feasibility, ensuring resources are optimally utilized. Precise bounding supports complexity analysis, enabling the determination of whether problems are tractable or require approximation methods.
Examples of Lower and Upper Bounds
Lower bounds represent the minimum limit or worst-case scenario for an algorithm's performance, such as O(n log n) for comparison-based sorting which establishes that no algorithm can sort faster than this in the general case. Upper bounds denote the maximum time or resource consumption an algorithm might require, like O(n^2) for bubble sort, ensuring it won't exceed this runtime. Examples include binary search with a lower bound of O(1) and an upper bound of O(log n), reflecting its best and worst-case complexities respectively.
Applications of Bounds in Computer Science
Lower bound and upper bound concepts are crucial in computer science for analyzing algorithm efficiency and performance limits. Lower bounds define the minimum time or space an algorithm requires to solve a problem, while upper bounds provide the maximum resources an algorithm will need in the worst case. These bounds guide the design and optimization of algorithms, ensuring feasibility and helping to identify computational complexity classes such as P, NP, and NP-complete.
Visualizing Bounds: Graphical Representation
Visualizing bounds involves plotting the lower bound and upper bound on a graph to illustrate the range within which a function, sequence, or dataset lies. The lower bound typically marks the minimum limit, while the upper bound indicates the maximum boundary, clearly defining the feasible region. This graphical representation aids in understanding convergence, error margins, and solution constraints in optimization and computational analysis.
Bounds in Optimization Problems
Bounds in optimization problems define the feasible region by specifying restrictions on variable values, where lower bounds set the minimum possible values and upper bounds establish the maximum limits. These constraints are crucial to ensure the solution satisfies all problem requirements and prevents the algorithm from exploring invalid or infinite regions. Properly defined bounds improve computational efficiency by reducing the search space and guiding optimization algorithms toward global or local optima within acceptable limits.
Summary: Choosing Between Lower and Upper Bounds
Lower bounds define the minimum performance or value guarantee for an algorithm or function, while upper bounds establish the maximum limit for its behavior. Selecting between lower and upper bounds depends on whether one aims to ensure a baseline performance or prevent worst-case scenarios. Understanding both bounds is crucial for optimizing algorithms, as it guides efficiency and robustness assessments within computational complexity or numerical analysis contexts.
Lower bound Infographic
 libterm.com
libterm.com