Arc is a versatile architectural element that enhances both structural integrity and aesthetic appeal in buildings, bridges, and doorways. Its curved design efficiently distributes weight, making it a crucial feature in engineering and construction projects. Explore how arcs can transform your space and learn about their various applications in the following article.
Table of Comparison
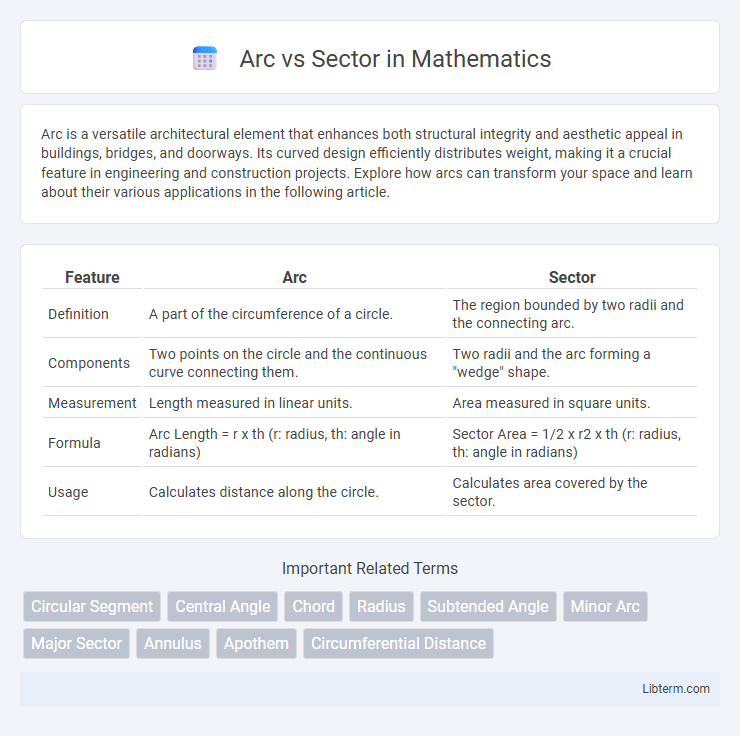
| Feature | Arc | Sector |
|---|---|---|
| Definition | A part of the circumference of a circle. | The region bounded by two radii and the connecting arc. |
| Components | Two points on the circle and the continuous curve connecting them. | Two radii and the arc forming a "wedge" shape. |
| Measurement | Length measured in linear units. | Area measured in square units. |
| Formula | Arc Length = r x th (r: radius, th: angle in radians) | Sector Area = 1/2 x r2 x th (r: radius, th: angle in radians) |
| Usage | Calculates distance along the circle. | Calculates area covered by the sector. |
Introduction to Arc vs Sector
An arc is a portion of the circumference of a circle defined by two endpoints, while a sector is the region enclosed by two radii and the corresponding arc. The arc measures the length along the circle's edge, whereas the sector represents the area within that segment. Understanding the distinction between arc length and sector area is essential for solving geometric problems related to circles.
Defining Arc in Geometry
An arc in geometry is a continuous portion of the circumference of a circle, defined by two endpoints on the circle. It measures the distance along the curved path between these two points and is often expressed in degrees or radians. Unlike a sector, which includes the area enclosed by two radii and their intercepted arc, an arc refers solely to the curved line segment itself.
Understanding the Sector of a Circle
The sector of a circle is a portion enclosed by two radii and the corresponding arc, representing a "slice" of the circle. Unlike an arc, which measures only the curved boundary length between two points on the circle, the sector includes the area between those points and the center. Understanding sectors is essential in calculating areas and angles related to pie charts, circular segments, and engineering designs involving circular components.
Key Differences Between Arc and Sector
An arc is a portion of the circumference of a circle defined by two endpoints, while a sector is the region enclosed by two radii and the arc between them. Arcs represent a one-dimensional curved line segment, whereas sectors cover a two-dimensional area of the circle. The measurement of an arc is given in degrees or radians as its central angle, whereas a sector's measurement includes both the central angle and the area bounded by the arc and radii.
Mathematical Formulas for Arc and Sector
The formula for the length of an arc is \( L = r\theta \), where \( r \) is the radius of the circle and \( \theta \) is the central angle in radians. The area of a sector is given by \( A = \frac{1}{2} r^2 \theta \), using the same parameters. Both formulas rely on the central angle \( \theta \) measured in radians to accurately describe the arc length and sector area in a circle.
Real-life Applications of Arcs
Arcs play a crucial role in engineering and architecture, particularly in designing bridges, arches, and domes where load distribution relies on curved structures. In automotive and aerospace industries, arcs are essential for creating aerodynamic shapes that reduce drag and enhance fuel efficiency. Additionally, arcs are integral in navigation systems and map-making for calculating distances along curved surfaces like the Earth's circumference.
Practical Uses of Sectors
Sectors are widely used in fields like engineering, architecture, and agriculture to calculate areas for design and land measurement. Unlike arcs, sectors provide precise information about the portion of a circle's area, essential for resource allocation and space planning. Practical applications include irrigation system design, pie chart creation, and determining land plots in circular layouts.
Visual Representation: Arc vs Sector
An arc is a curved line segment representing a portion of the circumference of a circle, while a sector is a geometric region enclosed by two radii and the arc between them. Visually, an arc appears as a simple curved boundary without enclosed area, whereas a sector resembles a pie-shaped wedge containing both the curved boundary and the two radii. The distinction is critical in geometry, with arcs defining length and sectors defining area within circular shapes.
Common Mistakes and Misconceptions
Many confuse an arc with a sector, mistakenly treating them as interchangeable; however, an arc is simply a portion of a circle's circumference, while a sector represents the area enclosed by two radii and the included arc. Another common mistake is to assume the length of an arc equals the perimeter of the sector, ignoring the radii that complete the sector's boundary. Misunderstandings also arise when calculating measurements, with errors in applying formulas for arc length \( L = r\theta \) (where \(\theta\) is in radians) versus sector area \( A = \frac{1}{2} r^2 \theta \).
Conclusion: Arc vs Sector – A Comparative Summary
An arc represents a portion of the circumference of a circle, measured in degrees or radians, while a sector is the area enclosed by two radii and the arc itself. Understanding the differences is crucial for accurate calculations in geometry, where arc length determines linear distance along the circle and sector area measures the two-dimensional space within the slice. Mastery of these concepts supports applications in fields like engineering, navigation, and computer graphics.
Arc Infographic
 libterm.com
libterm.com