A neutral Tannakian category is a rigid abelian tensor category equipped with a fiber functor to the category of vector spaces over a field, which allows it to be realized as the category of representations of an affine group scheme. This framework enables the study of group schemes through their linear representations and provides a powerful tool in algebraic geometry and number theory. Explore the rest of the article to understand how neutral Tannakian categories connect abstract categorical concepts with concrete algebraic structures.
Table of Comparison
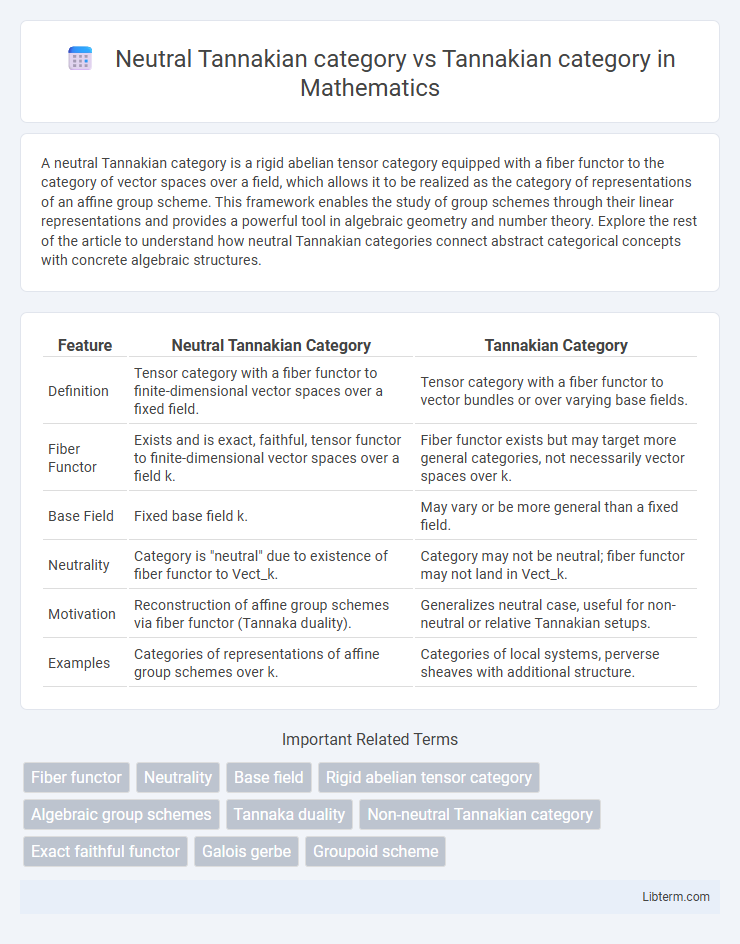
| Feature | Neutral Tannakian Category | Tannakian Category |
|---|---|---|
| Definition | Tensor category with a fiber functor to finite-dimensional vector spaces over a fixed field. | Tensor category with a fiber functor to vector bundles or over varying base fields. |
| Fiber Functor | Exists and is exact, faithful, tensor functor to finite-dimensional vector spaces over a field k. | Fiber functor exists but may target more general categories, not necessarily vector spaces over k. |
| Base Field | Fixed base field k. | May vary or be more general than a fixed field. |
| Neutrality | Category is "neutral" due to existence of fiber functor to Vect_k. | Category may not be neutral; fiber functor may not land in Vect_k. |
| Motivation | Reconstruction of affine group schemes via fiber functor (Tannaka duality). | Generalizes neutral case, useful for non-neutral or relative Tannakian setups. |
| Examples | Categories of representations of affine group schemes over k. | Categories of local systems, perverse sheaves with additional structure. |
Understanding Tannakian Categories
Neutral Tannakian categories refer to Tannakian categories equipped with a fiber functor to the category of vector spaces over a fixed field, allowing a direct reconstruction of an affine group scheme through Tannaka duality. General Tannakian categories may lack such a neutral fiber functor, requiring base change or extensions to realize the equivalence with the category of representations of an affine group scheme. Understanding these categories involves the study of tensor categories with rigid structures, fiber functors, and their representations, which connect algebraic geometry, group theory, and category theory in a unified framework.
Defining Neutral Tannakian Categories
Neutral Tannakian categories are Tannakian categories equipped with a fiber functor to the category of finite-dimensional vector spaces over a fixed field, enabling an equivalence with the category of representations of an affine group scheme. This fiber functor is a k-linear, exact, faithful, tensor functor that preserves the tensor structure and allows reconstruction of the group scheme via Tannaka duality. Unlike general Tannakian categories, which may lack a neutral fiber functor, neutral Tannakian categories provide a concrete realization of abstract tensor categories as representation categories of pro-algebraic groups.
Key Distinctions: Neutral vs Non-Neutral Tannakian
Neutral Tannakian categories admit a fiber functor to the category of finite-dimensional vector spaces over a base field, enabling an explicit equivalence with the category of representations of an affine group scheme over that field. Non-neutral Tannakian categories lack such a fiber functor over the base field, often requiring extension to a larger field or a more general tensor category for their fiber functor to exist. The key distinction lies in the existence of this fiber functor over the base field, which governs the realization and reconstruction of the underlying affine group scheme.
The Role of Fiber Functors in Neutrality
Neutral Tannakian categories are distinguished by the existence of a fiber functor to the category of finite-dimensional vector spaces over a fixed field, enabling a concrete realization of the category as representations of an affine group scheme. This fiber functor acts as a tensor exact faithful functor, providing a pivotal link that encodes the Tannakian category's abstract data into linear-algebraic terms, establishing neutrality. In contrast, general Tannakian categories may lack such a fiber functor defined over the base field, requiring extension of scalars or more complex constructions to achieve an equivalence with representation categories.
Structural Properties of Tannakian Categories
Neutral Tannakian categories are rigid abelian tensor categories equipped with a fiber functor to the category of finite-dimensional vector spaces over a fixed field, enabling their equivalence to the representation category of an affine group scheme. Tannakian categories, in general, require only a fiber functor to a more general neutral Tannakian category, lacking a fixed ground field, which reflects in their structural complexity and the absence of a canonical fiber functor. Key structural properties include the presence of duals, exact tensor functors, and rigidity, which ensure the reconstruction of group schemes from these categories through Tannaka duality.
Criteria for Neutrality in Tannakian Theory
Neutral Tannakian categories require the existence of a fiber functor to the category of finite-dimensional vector spaces over a fixed field, establishing an equivalence with the category of representations of an affine group scheme. The primary criterion for neutrality is the presence of a fiber functor defined over the base field, ensuring that the Tannakian category can be described by a pro-algebraic group scheme through Tannaka duality. In contrast, general Tannakian categories may only admit fiber functors over field extensions, lacking neutrality unless such a functor exists over the original base field.
Base Field Considerations and Neutral Tannakian Categories
Neutral Tannakian categories are defined over a specific base field \( k \) with a fiber functor taking values in finite-dimensional vector spaces over \( k \), enabling an equivalence with the category of representations of an affine group scheme over \( k \). In contrast, general Tannakian categories may lack a fiber functor over the base field itself, requiring extension to a larger field or algebraic closure to realize such an equivalence. The presence of a neutral fiber functor over the base field ensures the category is neutral Tannakian, highlighting the critical role of base field considerations in the classification and structure of Tannakian categories.
Applications of Neutral and Non-Neutral Tannakian Categories
Neutral Tannakian categories, characterized by the existence of a fiber functor to vector spaces over a fixed field, find crucial applications in decoding the representation theory of affine group schemes and facilitating the reconstruction of algebraic groups via Tannakian duality. Non-neutral Tannakian categories, lacking such a fiber functor, are pivotal in arithmetic geometry and the study of motives, where they model categories of sheaves or perverse sheaves without requiring a fixed base field. Both frameworks enable deep structural insights in areas such as algebraic geometry, number theory, and quantum groups, transforming categorical data into group-theoretic or geometric objects.
Examples Illustrating Neutral vs Non-Neutral Tannakian
Neutral Tannakian categories are characterized by the existence of a fiber functor to the category of vector spaces over the base field, facilitating a direct equivalence with the category of representations of an affine group scheme. Examples include the category of finite-dimensional representations of an affine group scheme over a field, such as the category of finite-dimensional representations of a reductive algebraic group over the complex numbers. Non-neutral Tannakian categories arise when there is no fiber functor to vector spaces over the base field but only after a field extension, as seen in certain categories of motives or variations of Hodge structures defined over non-algebraically closed fields.
Summary: Choosing Between Neutral and General Tannakian Categories
Neutral Tannakian categories are characterized by the existence of a fiber functor to the category of vector spaces over a field, enabling an equivalence with the category of representations of a pro-algebraic group. General Tannakian categories lack a specified fiber functor, requiring more complex approaches for reconstruction of associated group schemes. Choosing between neutral and general Tannakian categories depends on the availability of such fiber functors and the desired ease in category-group correspondence for applications in algebraic geometry and representation theory.
Neutral Tannakian category Infographic
 libterm.com
libterm.com