Matrix algebra forms the foundation of numerous applications in computer science, physics, and engineering by enabling efficient manipulation of arrays of numbers. It includes operations such as addition, multiplication, and finding determinants or inverses of matrices, which are critical for solving linear equations and transforming data sets. Explore this article to deepen your understanding of matrix algebra and its practical uses in various fields.
Table of Comparison
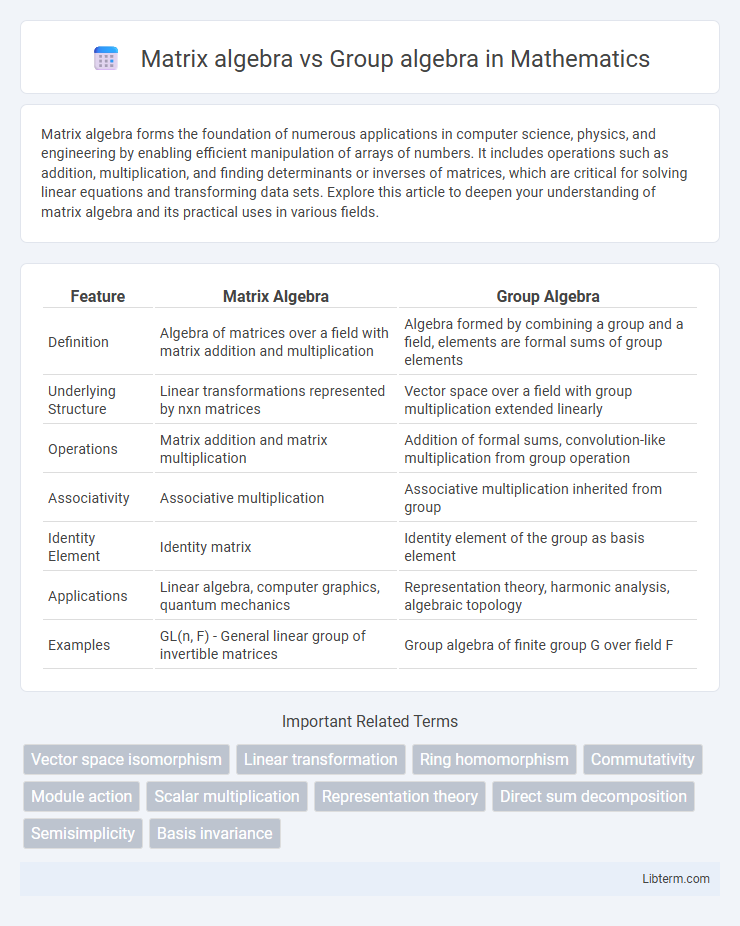
| Feature | Matrix Algebra | Group Algebra |
|---|---|---|
| Definition | Algebra of matrices over a field with matrix addition and multiplication | Algebra formed by combining a group and a field, elements are formal sums of group elements |
| Underlying Structure | Linear transformations represented by nxn matrices | Vector space over a field with group multiplication extended linearly |
| Operations | Matrix addition and matrix multiplication | Addition of formal sums, convolution-like multiplication from group operation |
| Associativity | Associative multiplication | Associative multiplication inherited from group |
| Identity Element | Identity matrix | Identity element of the group as basis element |
| Applications | Linear algebra, computer graphics, quantum mechanics | Representation theory, harmonic analysis, algebraic topology |
| Examples | GL(n, F) - General linear group of invertible matrices | Group algebra of finite group G over field F |
Introduction to Matrix Algebra and Group Algebra
Matrix algebra involves the study of matrices and operations such as addition, multiplication, and inversion that apply to these rectangular arrays of numbers, essential in solving linear equations and transforming geometric data. Group algebra combines group theory with algebraic structures, focusing on algebraic operations within a group and exploring elements paired with coefficients from a field or ring, often used in representation theory. Understanding matrix algebra provides computational tools for linear transformations, while group algebra offers a framework to analyze symmetries and abstract algebraic structures.
Fundamental Concepts: Definitions and Structures
Matrix algebra involves the study of matrices as linear transformations with operations including addition, multiplication, and inversion, forming a vector space over a field. Group algebra, constructed from a group and a field, combines group elements with field coefficients to form an algebraic structure that encodes group symmetries and supports convolution-like multiplication. Both structures emphasize different algebraic foundations: matrix algebra focuses on linearity and dimensionality, while group algebra centers on abstract group operations and their algebraic representations.
Key Differences Between Matrix Algebra and Group Algebra
Matrix algebra involves operations on matrices, including addition, multiplication, and inversion, primarily dealing with linear transformations and vector spaces. Group algebra extends a group's structure by forming linear combinations of group elements with coefficients from a field, capturing both algebraic and group properties in a unified framework. The key differences lie in matrix algebra's focus on numerical arrays and linear mappings, whereas group algebra emphasizes algebraic structures built from group elements and their scalar combinations.
Applications of Matrix Algebra in Mathematics and Science
Matrix algebra plays a crucial role in applications such as solving linear systems, computer graphics transformations, quantum mechanics, and data analysis through eigenvalues and eigenvectors. It enables efficient handling of large datasets and complex computations in fields like machine learning, physics, and engineering. The structured approach of matrix algebra facilitates the study of linear mappings and vector spaces, integral to mathematical modeling and scientific simulations.
Applications of Group Algebra in Abstract Algebra and Beyond
Group algebra serves as a fundamental bridge connecting abstract algebraic structures with linear representations, enabling the study of group actions on vector spaces. Its applications extend to character theory, representation theory, and the classification of finite groups, providing tools for analyzing symmetry in chemistry and physics. Moreover, group algebras facilitate the encoding of combinatorial and computational problems, proving essential in coding theory, cryptography, and the design of algorithms.
Dimensionality and Basis: Comparing Structures
Matrix algebra operates within vector spaces of fixed dimensionality determined by the size of the matrices, utilizing a canonical basis formed by matrix units with a single element equal to one and others zero. Group algebra extends group structures into algebraic frameworks by constructing linear combinations of group elements, where the dimensionality equals the order of the group and the basis consists of all group elements. The distinction lies in matrix algebra's dependence on matrix dimensions and standard basis, whereas group algebra's dimensionality and basis directly reflect the underlying group's cardinality and elements.
Operations: Multiplication, Addition, and Inverses
Matrix algebra involves operations such as matrix multiplication, addition, and finding inverses, where multiplication is generally non-commutative and inverses exist only for invertible matrices. Group algebra, constructed from a group and a field, combines group elements with coefficients through addition and convolution-like multiplication, ensuring associativity and the existence of inverses based on group properties. The key difference lies in matrix algebra's structure as a vector space with linear transformations, while group algebra forms an algebra over a field that encodes the group's multiplicative structure.
Representations and Modules: Bridging the Algebras
Matrix algebra and group algebra connect deeply through the study of representations and modules, where matrix algebra provides concrete realizations of abstract group elements as linear transformations on vector spaces. Representations of groups can be viewed as modules over the group algebra, facilitating the translation of group operations into matrix multiplication frameworks. This interplay allows for powerful algebraic techniques to analyze group structures using matrix methods, enhancing the understanding of both algebraic systems.
Examples Demonstrating Practical Use Cases
Matrix algebra finds practical application in computer graphics, enabling transformations like rotations and scaling through matrix multiplication. Group algebra, exemplified by permutations in the symmetric group, is essential in cryptography for encoding and decoding messages based on group operations. Both algebras underpin quantum mechanics, with matrix algebra representing observables and group algebra describing symmetries in particle physics.
Summary: Choosing Between Matrix Algebra and Group Algebra
Matrix algebra excels in representing linear transformations and solving systems of linear equations through operations on arrays of numbers, offering concrete computational methods. Group algebra provides a framework for studying algebraic structures by extending groups into vector spaces, facilitating analysis of symmetry and abstract algebraic properties. Selecting between matrix algebra and group algebra depends on whether the focus is practical computation and applications in linear systems or theoretical exploration of group properties and representation theory.
Matrix algebra Infographic
 libterm.com
libterm.com