A probability measure quantifies the likelihood of events within a given sample space, assigning values between 0 and 1 to ensure consistency with probability axioms. This mathematical function underpins statistical analysis, enabling precise modeling of random phenomena and informed decision-making. Explore the rest of the article to deepen your understanding of how probability measures shape predictions and uncertainty assessments.
Table of Comparison
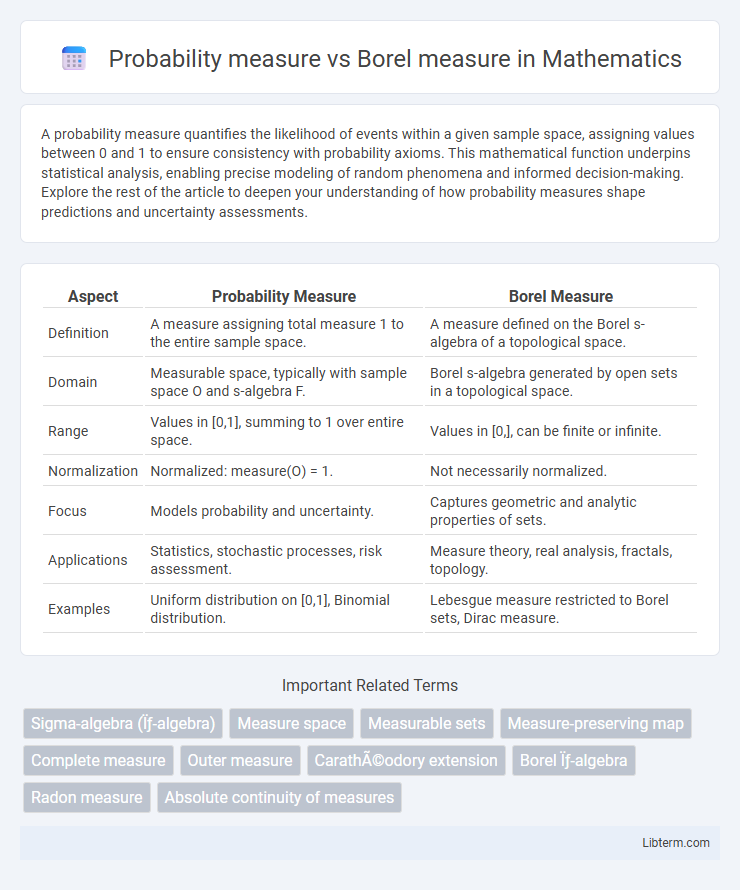
| Aspect | Probability Measure | Borel Measure |
|---|---|---|
| Definition | A measure assigning total measure 1 to the entire sample space. | A measure defined on the Borel s-algebra of a topological space. |
| Domain | Measurable space, typically with sample space O and s-algebra F. | Borel s-algebra generated by open sets in a topological space. |
| Range | Values in [0,1], summing to 1 over entire space. | Values in [0,], can be finite or infinite. |
| Normalization | Normalized: measure(O) = 1. | Not necessarily normalized. |
| Focus | Models probability and uncertainty. | Captures geometric and analytic properties of sets. |
| Applications | Statistics, stochastic processes, risk assessment. | Measure theory, real analysis, fractals, topology. |
| Examples | Uniform distribution on [0,1], Binomial distribution. | Lebesgue measure restricted to Borel sets, Dirac measure. |
Introduction to Probability Measures and Borel Measures
Probability measures assign values between 0 and 1 to events within a sigma-algebra, ensuring the total measure of the sample space is 1, which formalizes the concept of probability in measure theory. Borel measures are measures defined on the Borel sigma-algebra generated by open sets in a topological space, commonly used to measure subsets of real numbers and support various applications in analysis and probability. Understanding the distinction between probability measures and Borel measures is crucial for grasping how different measures are constructed and applied on measurable spaces, particularly in probability theory and real analysis.
Defining Probability Measures: Foundations and Properties
Probability measures are specialized Borel measures defined on a sigma-algebra of subsets within a measurable space, assigning a total measure of one to the entire sample space, ensuring normalization. These measures satisfy countable additivity, meaning the measure of a countable union of disjoint sets equals the sum of their measures, establishing a foundation for probability theory. Key properties include non-negativity, sigma-additivity, and total measure unity, making probability measures essential for modeling random phenomena in measure-theoretic probability.
Understanding Borel Measures: Basic Concepts
Borel measures are defined on the s-algebra generated by open sets in a topological space, allowing the measurement of Borel sets, which include intervals and more complex constructions. Probability measures are a specific type of Borel measure with total measure equal to one, making them essential for modeling random phenomena on spaces like the real line. Understanding Borel measures involves grasping concepts of s-algebras, outer measures, and the Caratheodory extension theorem, which ensures the consistent extension of measures from simpler sets to the full Borel s-algebra.
Key Differences Between Probability Measures and Borel Measures
Probability measures assign a total mass of one to the entire space, ensuring that probabilities sum up to one by definition, while Borel measures are more general and can assign infinite or finite values to Borel sets without this normalization constraint. Probability measures are defined on sigma-algebras generated by Borel sets, often called Borel sigma-algebras, specifically for probabilistic applications, whereas Borel measures encompass any measure defined on Borel sigma-algebras regardless of total measure or probabilistic interpretation. Key differences include the normalization property unique to probability measures and the broader applicability of Borel measures in various mathematical and analytical contexts beyond probability theory.
The Role of Sigma-Algebras in Measure Theory
Sigma-algebras provide the foundational structure for both probability measures and Borel measures by defining the collection of measurable sets on which these measures operate. In probability theory, sigma-algebras ensure that probability measures assign consistent probabilities to events, enabling the rigorous handling of random phenomena. For Borel measures, sigma-algebras generated by open sets in a topological space allow the extension of measures to complex sets while preserving countable additivity and measurability.
Applications of Probability Measures in Statistics
Probability measures quantify the likelihood of events within a sample space, providing a foundational framework for statistical inference, hypothesis testing, and predictive modeling. Borel measures, defined on Borel s-algebras generated by open sets in topological spaces, enable the rigorous treatment of continuous random variables and integration over complex event spaces. In statistics, probability measures facilitate the formulation of distributions, expectation values, and variance calculations crucial for parameter estimation, confidence intervals, and stochastic process analysis.
Borel Measures in Real Analysis and Topology
Borel measures in real analysis and topology assign measures to Borel s-algebras generated by open sets in topological spaces, providing a framework for integrating functions over these spaces. Unlike probability measures, which are finitely additive with total measure one, Borel measures can be infinite and are essential for studying properties of continuous functions and convergence in metric spaces. These measures enable detailed analysis of measurable sets and support key theorems such as the Riesz Representation Theorem, linking measures with continuous linear functionals on spaces of continuous functions.
Comparing Measurability: Probability vs. Borel Contexts
Probability measures assign values within the unit interval [0,1] to sets in a sigma-algebra, typically focusing on events in a probability space, while Borel measures are defined on Borel sigma-algebras generated by open sets in topological spaces, capturing a broader class of measurable sets. The measurability in probability contexts often hinges on events relevant to stochastic processes or random variables, emphasizing sigma-algebras compatible with probability distributions. Borel measures encompass more extensive topological structures, allowing for detailed measure assignments beyond probabilistic interpretations, crucial in analysis and geometry.
Example Scenarios: When to Use Probability or Borel Measures
Probability measures are used when modeling random events with total measure one, such as determining the likelihood of outcomes in coin tosses or stock price movements. Borel measures apply in scenarios requiring measure assignment to all Borel sets in a topological space, like analyzing Lebesgue measure on real intervals or defining measures on fractal sets. Choose probability measures for probabilistic events with normalized outcomes, and Borel measures for more general geometric or analytic measure assignments beyond probability contexts.
Conclusion: Choosing the Appropriate Measure
Selecting the appropriate measure depends on the context and purpose of the analysis. Probability measures are ideal for modeling random experiments and probabilistic events, ensuring total measure equals one, while Borel measures provide a broader framework for measuring subsets in topological spaces, particularly in real analysis. Understanding the specific requirements of the problem, such as normalization in probability or measure-theoretic properties in analysis, guides the choice between a probability measure and a Borel measure.
Probability measure Infographic
 libterm.com
libterm.com