The Stiefel-Whitney class is a fundamental concept in algebraic topology that assigns cohomology classes to real vector bundles, revealing crucial information about their structure and properties. These characteristic classes help detect whether bundles are orientable and provide insights into their topological invariants. Explore the rest of the article to understand how Stiefel-Whitney classes influence manifold theory and applications in geometry.
Table of Comparison
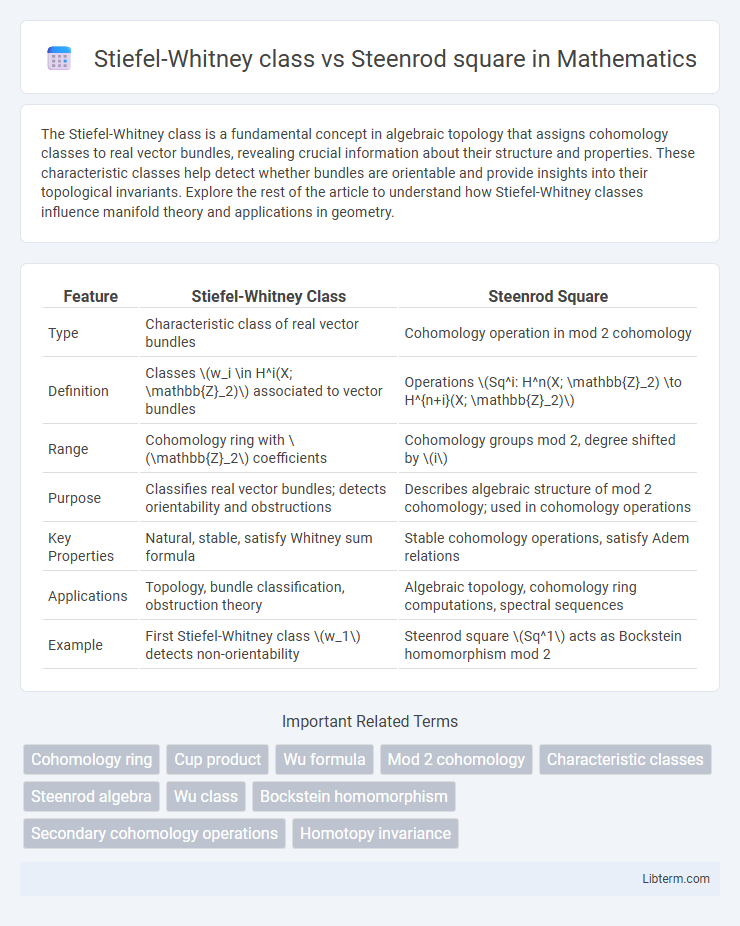
| Feature | Stiefel-Whitney Class | Steenrod Square |
|---|---|---|
| Type | Characteristic class of real vector bundles | Cohomology operation in mod 2 cohomology |
| Definition | Classes \(w_i \in H^i(X; \mathbb{Z}_2)\) associated to vector bundles | Operations \(Sq^i: H^n(X; \mathbb{Z}_2) \to H^{n+i}(X; \mathbb{Z}_2)\) |
| Range | Cohomology ring with \(\mathbb{Z}_2\) coefficients | Cohomology groups mod 2, degree shifted by \(i\) |
| Purpose | Classifies real vector bundles; detects orientability and obstructions | Describes algebraic structure of mod 2 cohomology; used in cohomology operations |
| Key Properties | Natural, stable, satisfy Whitney sum formula | Stable cohomology operations, satisfy Adem relations |
| Applications | Topology, bundle classification, obstruction theory | Algebraic topology, cohomology ring computations, spectral sequences |
| Example | First Stiefel-Whitney class \(w_1\) detects non-orientability | Steenrod square \(Sq^1\) acts as Bockstein homomorphism mod 2 |
Introduction to Stiefel-Whitney Classes and Steenrod Squares
Stiefel-Whitney classes are characteristic classes associated with real vector bundles, providing topological invariants that detect obstructions to finding non-vanishing sections. Steenrod squares are cohomology operations defined in mod 2 cohomology, acting on cohomology classes to produce new invariants that capture finer algebraic structures. The interplay between Stiefel-Whitney classes and Steenrod squares reveals deep relationships in algebraic topology, where Steenrod squares can describe properties of Stiefel-Whitney classes and enhance the study of vector bundle classification.
Historical Background and Mathematical Context
The Stiefel-Whitney classes, introduced by Eduard Stiefel and Hassler Whitney in the 1930s, represent characteristic classes that assign to each real vector bundle a sequence of cohomology classes with coefficients in Z/2Z, capturing topological invariants such as orientability and obstruction to the existence of sections. Steenrod squares, developed by Norman Steenrod in the mid-1940s, are cohomology operations acting on mod 2 cohomology and provide a key tool for algebraic topologists to study the structure of cohomology rings and relations between characteristic classes. The interplay between Stiefel-Whitney classes and Steenrod squares is fundamental in algebraic topology, where Steenrod squares are used to express relations and calculate the Stiefel-Whitney classes, thus deepening the understanding of vector bundles and manifold invariants.
Fundamental Definitions: Stiefel-Whitney Classes
Stiefel-Whitney classes are characteristic classes associated with real vector bundles, defined as elements in the mod 2 cohomology ring that measure the nontriviality of these bundles. They provide obstructions to the existence of certain sections and orientations, encoding topological information about vector bundles over a given base space. Steenrod squares are cohomology operations acting on mod 2 cohomology classes, and they interact with Stiefel-Whitney classes by providing algebraic tools to compute and understand these characteristic classes.
Core Concepts: Steenrod Squares Explained
Steenrod squares are cohomology operations that act on the mod 2 cohomology of topological spaces, providing algebraic invariants essential in algebraic topology. Stiefel-Whitney classes are characteristic classes associated with real vector bundles, constructed using Steenrod squares to capture information about the bundle's orientability and structure. The interaction between Steenrod squares and Stiefel-Whitney classes allows the computation of cohomological invariants that detect subtle geometric and topological properties of manifolds.
Algebraic Structure and Properties Comparison
Stiefel-Whitney classes are characteristic classes associated with real vector bundles, providing cohomology classes in mod 2 cohomology that capture topological information about the bundle's structure. Steenrod squares form a family of stable cohomology operations acting on mod 2 cohomology groups, with algebraic properties defined by the Adem relations and Cartan formula, enabling the construction of new cohomology classes from existing ones. The interaction between Stiefel-Whitney classes and Steenrod squares is fundamental, with Steenrod squares generating relations among Stiefel-Whitney classes and revealing deeper algebraic invariants in the cohomology ring.
Interactions: Steenrod Squares Acting on Stiefel-Whitney Classes
Steenrod squares act naturally on Stiefel-Whitney classes, revealing intricate algebraic structures in the cohomology of topological spaces. Specifically, the Steenrod square operations Sq^i applied to a Stiefel-Whitney class w_j satisfy the Wu formula, linking Sq^i(w_j) to sums of Stiefel-Whitney classes and exposing their role in characteristic class theory. This interaction enables the calculation of secondary characteristic classes and encodes geometric information about vector bundles and manifolds.
Applications in Topology and Geometry
Stiefel-Whitney classes provide essential invariants that classify vector bundles and detect obstructions to sections, critical in manifold theory and characteristic class calculations. Steenrod squares act as cohomology operations that refine invariants derived from Stiefel-Whitney classes, enabling the detection of subtle topological properties and facilitating computations in mod 2 cohomology rings. Together, they underpin major results in obstruction theory, characteristic classes, and the topology of fiber bundles, influencing fields like surgery theory and immersion problems.
Computational Examples and Key Results
Stiefel-Whitney classes and Steenrod squares both play fundamental roles in algebraic topology, particularly in characteristic class computation and cohomology operations. Computational examples frequently illustrate the application of Steenrod squares on Stiefel-Whitney classes, such as the relation Sq^i(w_j) = _{k=0}^i \binom{j-k}{i-k} w_{j-k} w_k, which encodes how Steenrod squares act on these characteristic classes. Key results include the Wu formula, which links Steenrod squares to Stiefel-Whitney classes via the Wu classes, enabling effective calculation of characteristic classes in smooth manifolds.
Differences and Similarities: A Comparative Analysis
Stiefel-Whitney classes and Steenrod squares both arise in algebraic topology as cohomology operations related to vector bundles and manifold invariants, but they differ fundamentally in their construction and applications. Stiefel-Whitney classes are characteristic classes defined for real vector bundles capturing obstruction information in mod 2 cohomology, while Steenrod squares are cohomology operations acting on mod 2 cohomology rings, generalizing the cup product structure. Both share compatibility in mod 2 cohomology and engage with topological invariants, yet Stiefel-Whitney classes provide geometric bundle data, whereas Steenrod squares function as algebraic tools to manipulate cohomological classes.
Conclusion: Significance in Modern Algebraic Topology
Stiefel-Whitney classes serve as fundamental invariants characterizing vector bundles and their orientability, while Steenrod squares form a family of cohomology operations enriching the algebraic structure of cohomology rings. The interaction between these constructs enables deeper insight into the topology of manifolds, facilitating classification problems and detecting subtle geometric properties. Their combined significance underpins modern advances in algebraic topology, influencing fields such as cobordism theory and homotopy theory.
Stiefel-Whitney class Infographic
 libterm.com
libterm.com