Covering space refers to the concept in topology where one space maps onto another in a way that locally resembles a direct product, allowing complex shapes to be studied through simpler, overlapping pieces. Understanding covering spaces is crucial for analyzing fundamental groups and unraveling properties of geometric structures. Dive into the rest of the article to explore how covering spaces unlock powerful tools for your mathematical toolkit.
Table of Comparison
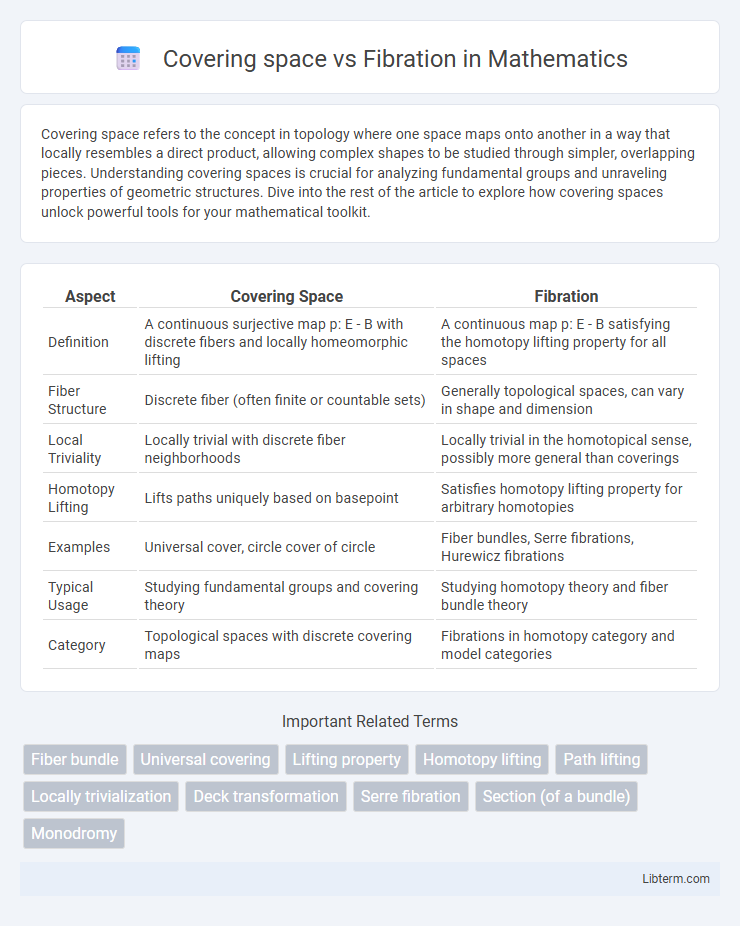
| Aspect | Covering Space | Fibration |
|---|---|---|
| Definition | A continuous surjective map p: E - B with discrete fibers and locally homeomorphic lifting | A continuous map p: E - B satisfying the homotopy lifting property for all spaces |
| Fiber Structure | Discrete fiber (often finite or countable sets) | Generally topological spaces, can vary in shape and dimension |
| Local Triviality | Locally trivial with discrete fiber neighborhoods | Locally trivial in the homotopical sense, possibly more general than coverings |
| Homotopy Lifting | Lifts paths uniquely based on basepoint | Satisfies homotopy lifting property for arbitrary homotopies |
| Examples | Universal cover, circle cover of circle | Fiber bundles, Serre fibrations, Hurewicz fibrations |
| Typical Usage | Studying fundamental groups and covering theory | Studying homotopy theory and fiber bundle theory |
| Category | Topological spaces with discrete covering maps | Fibrations in homotopy category and model categories |
Introduction to Covering Spaces and Fibrations
Covering spaces are topological spaces that map onto another space in a locally trivial way, with discrete fibers resembling "sheets" that locally look like a product space, fundamental in studying the fundamental group and lifting properties. Fibrations generalize covering spaces by allowing fibers to vary continuously and possessing a homotopy lifting property critical for fiber bundle theory and homotopy theory. Both concepts play essential roles in algebraic topology, with covering spaces serving as special cases of fibrations where the fiber is discrete and the base space is path-connected.
Fundamental Concepts and Definitions
Covering spaces involve a continuous surjective map p: E - B where for every point b in B, there exists an open neighborhood U such that p-1(U) is a disjoint union of open sets in E, each homeomorphic to U, emphasizing the local triviality and unique path lifting property. Fibrations generalize this idea, defined by a map p: E - B satisfying the homotopy lifting property for every space X, ensuring that homotopies in B can be lifted to E, with fibrations often characterized by their fibers and homotopy-theoretic behavior. The fundamental group plays a central role in covering space theory through monodromy actions, while fibrations extend these concepts to more flexible homotopy contexts, making them essential in algebraic topology for studying fiber bundles and spectral sequences.
Historical Background and Development
Covering spaces emerged in the early 20th century through the works of mathematicians like Heinz Hopf and Eduard Cech, providing foundational tools for studying topological spaces via locally homeomorphic projections. Fibrations evolved later from the concept of fiber bundles in the mid-20th century, notably formalized by Jean-Pierre Serre, to systematically explore homotopy-theoretic properties and generalize covering space theory. The development of fibrations significantly expanded algebraic topology by enabling the analysis of spaces with complex local-to-global structures beyond those addressed by classical covering space theory.
Key Differences Between Covering Spaces and Fibrations
Covering spaces are special types of fibrations where the fiber is discrete and the projection map is a local homeomorphism, ensuring each point in the base space has an evenly covered neighborhood. Fibrations generalize covering spaces by allowing fibers to be more complex topological spaces and requiring only the homotopy lifting property, which provides stronger control over homotopies but weaker local triviality conditions. Key differences include the discreteness of fibers in coverings versus the potentially continuous structure of fibers in fibrations, and the fact that coverings guarantee a fixed number of sheets locally, while fibrations may have varying fiber structure depending on the base space.
Properties and Examples of Covering Spaces
Covering spaces are topological spaces that project onto another space via a continuous surjective map with discrete fibers, preserving local homeomorphisms, unlike fibrations which allow more flexible lifting properties without requiring local triviality over discrete fibers. Key properties of covering spaces include path lifting, unique lifting of homotopies, and local triviality over evenly covered neighborhoods, exemplified by the classic covering of the circle \( S^1 \) by the real line \( \mathbb{R} \) or the universal cover of a topological space. These properties distinguish covering spaces in algebraic topology, facilitating computations of fundamental groups and classification of connected covers through group actions.
Properties and Examples of Fibrations
Fibrations generalize covering spaces by allowing fibers with varying topology, characterized by the homotopy lifting property essential for algebraic topology and homotopy theory. Key properties include the existence of a continuous map p: E - B with the homotopy lifting property for every space, making fibrations fundamental in the study of fiber bundles and Serre fibrations. Typical examples are fiber bundles like the Hopf fibration S^3 - S^2 with fiber S^1, which illustrates nontrivial topology beyond covering spaces that have discrete fibers and local homeomorphisms.
Homotopy Lifting and Path Lifting Properties
Covering spaces guarantee unique path lifting and homotopy lifting properties due to their discrete fiber structure and local homeomorphisms onto the base space, ensuring every path or homotopy in the base uniquely lifts to the covering space. Fibrations generalize this concept by allowing continuous lifting of homotopies, characterized by the homotopy lifting property (HLP) with respect to all spaces, but path lifting in fibrations may not be unique without additional conditions such as the fiber being a homotopy fiber. The distinction lies in uniqueness: covering spaces provide unique lifts for paths and homotopies, while fibrations ensure existence of lifts, crucial for analyzing fiber bundle structures and homotopy-theoretic invariants.
Applications in Topology and Geometry
Covering spaces provide fundamental tools in algebraic topology for studying the properties of spaces via their universal covers and deck transformations, enabling classification of surfaces and analysis of fundamental groups. Fibrations extend these concepts by incorporating homotopy lifting properties, crucial for fiber bundle theory and spectral sequences that facilitate computations in homotopy and cohomology groups. Applications in geometry include the use of covering spaces for analyzing Riemann surfaces and orbifolds, while fibrations underpin modern approaches to fiber bundles, characteristic classes, and classification problems in differential geometry.
Interrelations and Overlapping Features
Covering spaces and fibrations both serve as fundamental constructions in algebraic topology that enable the study of continuous mappings with specific lifting properties. Covering spaces are characterized by locally trivial projections admitting unique path-lifting, while fibrations generalize this concept through homotopy lifting properties, often captured by the Serre or Hurewicz axioms. The overlap arises in instances where covering spaces act as particular cases of fibrations with discrete fibers, highlighting deep interrelations in fiber bundle theory and homotopy theory frameworks.
Choosing Between Covering Space and Fibration Approaches
Choosing between covering space and fibration approaches depends on the topological complexity and the homotopical information required. Covering spaces are ideal for studying discrete symmetries and fundamental groups, providing simple local homeomorphisms with evenly covered neighborhoods. Fibrations generalize this by capturing fiber bundle structures with homotopy lifting properties, making them suitable for analyzing continuous variation of fibers over a base space in homotopy theory.
Covering space Infographic
 libterm.com
libterm.com