Lebesgue measure is a fundamental concept in real analysis that generalizes the notion of length, area, and volume to more complex sets than simple intervals. It provides a rigorous way to assign a "size" to subsets of Euclidean space, making it essential for integration theory and probability. Explore the rest of the article to understand how Lebesgue measure underpins modern mathematical analysis and its applications.
Table of Comparison
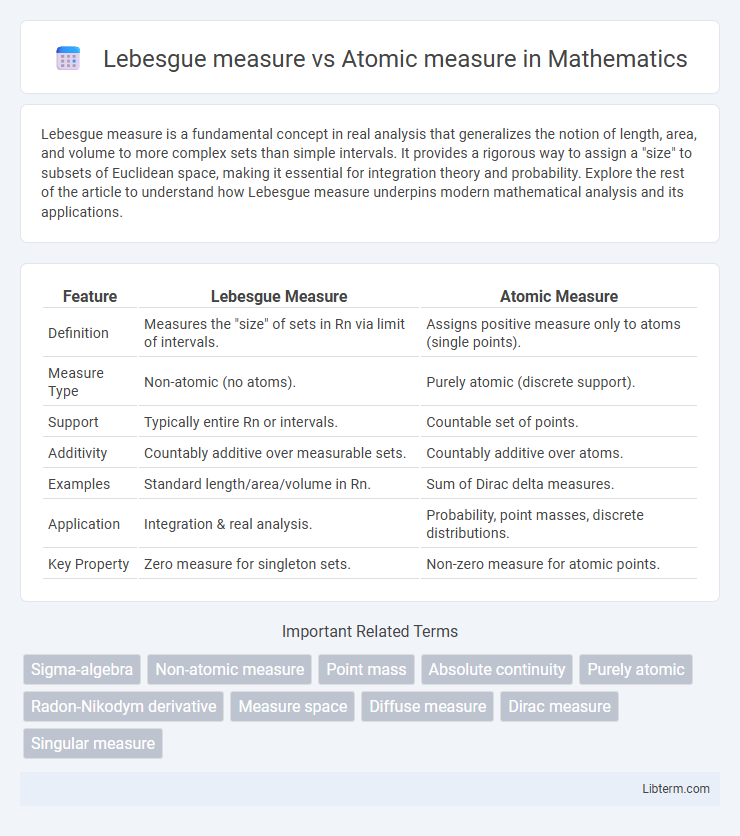
| Feature | Lebesgue Measure | Atomic Measure |
|---|---|---|
| Definition | Measures the "size" of sets in Rn via limit of intervals. | Assigns positive measure only to atoms (single points). |
| Measure Type | Non-atomic (no atoms). | Purely atomic (discrete support). |
| Support | Typically entire Rn or intervals. | Countable set of points. |
| Additivity | Countably additive over measurable sets. | Countably additive over atoms. |
| Examples | Standard length/area/volume in Rn. | Sum of Dirac delta measures. |
| Application | Integration & real analysis. | Probability, point masses, discrete distributions. |
| Key Property | Zero measure for singleton sets. | Non-zero measure for atomic points. |
Introduction to Measure Theory
Lebesgue measure is a fundamental concept in measure theory that assigns a non-negative size to subsets of Euclidean space, capturing the intuitive notion of length, area, and volume. Atomic measures, in contrast, concentrate mass on countable sets called atoms, where each atom has a positive measure and the measure of any subset without atoms is zero. Understanding the distinction between Lebesgue and atomic measures is crucial for analyzing measurable functions, integration, and the decomposition of measures in advanced mathematical analysis.
Understanding the Lebesgue Measure
Lebesgue measure formalizes the concept of "length" for subsets of the real line, extending beyond simple intervals to more complex sets by assigning a non-negative real number representing their size. Unlike atomic measures, which concentrate mass on individual points or atoms, Lebesgue measure is nonatomic, meaning it assigns zero measure to singletons and distributes measure continuously across intervals. This distinction allows Lebesgue measure to effectively analyze and integrate functions with respect to continuous distributions, making it fundamental in real analysis and probability theory.
Defining Atomic Measure
Atomic measure is a type of measure defined by the presence of atoms, which are measurable sets with positive measure that contain no smaller subsets of positive measure. Unlike Lebesgue measure, which is nonatomic and assigns zero measure to singletons, atomic measures concentrate mass on discrete points or atoms. This fundamental difference makes atomic measures ideal for modeling phenomena with distinct, isolated values, whereas Lebesgue measure excels in continuous settings.
Key Differences Between Lebesgue and Atomic Measures
Lebesgue measure assigns sizes to subsets of real numbers based on length, accommodating both continuous intervals and more complex sets, whereas atomic measure concentrates on discrete points with positive measure, called atoms. Lebesgue measure is nonatomic, meaning no single point has positive measure, while atomic measures are purely atomic, assigning all measure to individual points. This fundamental difference makes Lebesgue measure ideal for analyzing continuous phenomena and atomic measures suitable for discrete distributions.
Properties of Lebesgue Measure
Lebesgue measure is a complete, translation-invariant measure defined on the s-algebra of Lebesgue measurable sets in Rn, assigning measure zero to singletons, contrasting with atomic measures that concentrate positive measure on individual points. It is countably additive, respects monotonicity, and is regular, meaning measurable sets can be approximated by open or closed sets in terms of measure. These properties ensure Lebesgue measure provides a rigorous foundation for integration and probability theory, particularly in continuous spaces.
Properties of Atomic Measure
Atomic measures assign positive measure to singletons, making them purely discrete with support contained in countable sets, contrasting with Lebesgue measure's nonatomic, continuous nature. These measures are s-additive and concentrate mass on isolated points, enabling precise quantification of atoms in measurable spaces. Atomic measures lack translation invariance and do not assign measure to intervals like Lebesgue measure but fully characterize measures supported on countable atomic sets.
Examples Illustrating Each Measure
The Lebesgue measure assigns a nonzero measure to intervals like [0,1], capturing the "length" of continuous sets and exemplified by the measure of the unit interval as 1. Atomic measures concentrate mass at discrete points, such as the Dirac measure d_x, which assigns measure 1 to the singleton set {x} and 0 elsewhere. These examples highlight the Lebesgue measure's ability to quantify "volume" over continuous domains versus atomic measures' focus on isolated points.
Applications in Real Analysis
Lebesgue measure is fundamental in real analysis for integrating functions over continuous intervals, enabling the rigorous treatment of limits and convergence in spaces like L^p. Atomic measures concentrate mass on discrete points, playing a crucial role in probability theory and spectral analysis by representing distributions with isolated atoms. Applications of Lebesgue measure dominate in differentiation and integration theory, while atomic measures are essential in studying singular measures and decomposing measures into discrete and continuous parts.
Implications in Probability and Statistics
Lebesgue measure, as a continuous measure, allows for the modeling of probabilities over continuous sample spaces, enabling the application of integral-based techniques in probability theory and statistical inference. Atomic measures concentrate probability mass on discrete points, facilitating analysis of discrete random variables and simplifying computations in scenarios such as count data or categorical distributions. Understanding these differences impacts the choice of probability models, influences the formulation of likelihood functions, and determines the applicability of statistical methods like density estimation or hypothesis testing.
Conclusion: Choosing the Right Measure
Choosing between Lebesgue measure and atomic measure depends on the nature of the set being studied and the type of analysis required. Lebesgue measure excels in applications involving continuous data and intervals because it can accurately quantify the "size" of subsets of Euclidean space, while atomic measures are ideal for discrete or countable sets where the measure is concentrated on isolated points. Understanding the underlying structure of the space allows for selecting the measure that best captures the essential properties, ensuring precise integration and probability calculations.
Lebesgue measure Infographic
 libterm.com
libterm.com