A null set, also known as an empty set, contains no elements and is symbolized by {} or in mathematics. Understanding the properties and significance of null sets is essential for grasping foundational concepts in set theory and logic. Discover how this fundamental idea influences various mathematical principles by reading the rest of the article.
Table of Comparison
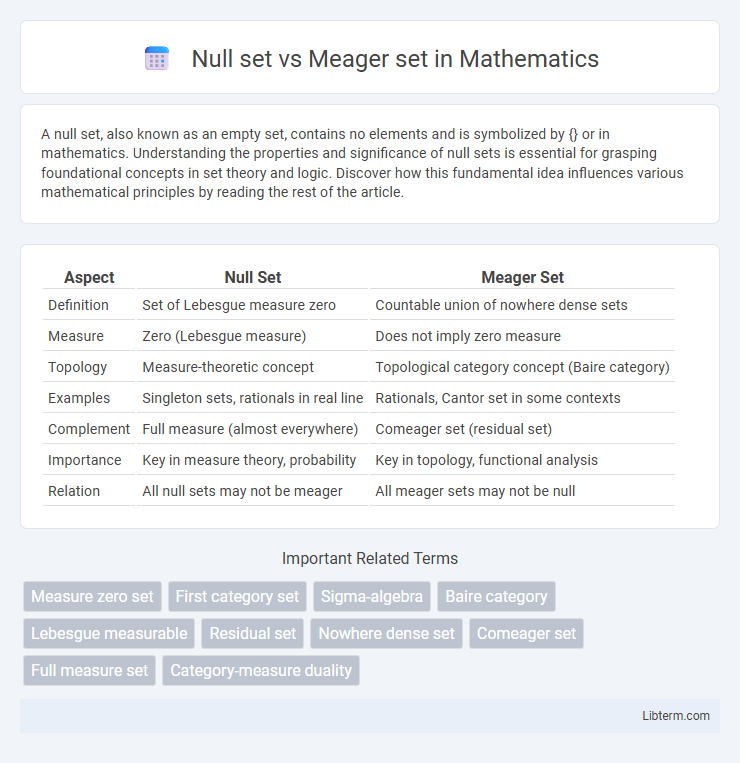
| Aspect | Null Set | Meager Set |
|---|---|---|
| Definition | Set of Lebesgue measure zero | Countable union of nowhere dense sets |
| Measure | Zero (Lebesgue measure) | Does not imply zero measure |
| Topology | Measure-theoretic concept | Topological category concept (Baire category) |
| Examples | Singleton sets, rationals in real line | Rationals, Cantor set in some contexts |
| Complement | Full measure (almost everywhere) | Comeager set (residual set) |
| Importance | Key in measure theory, probability | Key in topology, functional analysis |
| Relation | All null sets may not be meager | All meager sets may not be null |
Introduction to Null Sets and Meager Sets
Null sets, also known as sets of measure zero, consist of points in a space whose total Lebesgue measure is zero, making them negligible in terms of volume. Meager sets, or sets of first category, are formed by countable unions of nowhere dense sets, indicating their topological smallness despite possibly having positive measure. Understanding null and meager sets is crucial in measure theory and topology, as they capture distinct notions of smallness--measure-theoretic and category-theoretic, respectively.
Formal Definitions: Null Sets vs Meager Sets
Null sets, defined in measure theory, are subsets of a given measure space that have measure zero, meaning their total "size" in terms of the measure is negligible. Meager sets, in contrast, arise in topology and are defined as countable unions of nowhere dense sets, representing sets that are "small" in the sense of category rather than measure. While null sets focus on measure and size, meager sets emphasize topological denseness and category, leading to different notions of "smallness" in mathematical analysis.
Measure Theory: Understanding Null Sets
Null sets in measure theory are subsets of a measure space with measure zero, meaning they are "negligible" in terms of volume or size under a given measure, often the Lebesgue measure on real numbers. Meager sets, also called sets of the first category, are topologically small, being countable unions of nowhere dense sets, but not necessarily having measure zero. Understanding null sets emphasizes their significance in integration and probability theory, where events of measure zero can be ignored for practical purposes, contrasting with meager sets that relate more to topological properties rather than measure.
Category Theory: Understanding Meager Sets
In category theory, meager sets are defined as countable unions of nowhere dense sets, representing "small" or "thin" sets in a topological space, distinct from null sets which measure size in terms of measure zero. Meager sets capture the notion of topological "smallness" versus the measure-theoretic "smallness" of null sets, providing insight into the Baire category theorem and its implications in analysis and topology. Understanding meager sets in category theory helps analyze the structure of spaces where traditional measures fail to classify exceptional sets effectively.
Key Differences Between Null and Meager Sets
Null sets are subsets of a measure space with Lebesgue measure zero, meaning they occupy no volume in terms of measure theory. Meager sets, also known as sets of the first category, are subsets of a topological space that can be expressed as a countable union of nowhere dense sets, emphasizing their topological smallness rather than measure. The key difference lies in their defining properties: null sets are measure-theoretic constructs with zero measure, while meager sets are topological constructs characterized by their lack of density in any open set.
Examples of Null Sets in Real Analysis
Null sets in real analysis include classic examples such as the Cantor set, which has Lebesgue measure zero despite being uncountably infinite. Finite and countable sets, like the set of rational numbers within any interval, also qualify as null sets due to their measure zero property. These examples illustrate how null sets differ from meager sets, which are defined by topological size rather than measure.
Examples of Meager Sets in Topology
Meager sets in topology include countable unions of nowhere dense sets, such as the rationals in the real numbers, which form a classic example of a meager set despite having Lebesgue measure zero as well. Another example is the set of all sequences with finitely many nonzero terms in the space of all real sequences, demonstrating how meager sets can be large in cardinality but "small" in topological structure. Unlike null sets that focus on measure, meager sets emphasize category, highlighting the difference between measure-theoretic smallness and topological smallness.
Intersection and Union Properties
Null sets, defined by having Lebesgue measure zero, and meager sets, characterized as countable unions of nowhere dense sets, exhibit distinct intersection and union properties. The intersection of countably many null sets remains a null set, while the union of countably many null sets also has measure zero, preserving the null property under countable operations. In contrast, the intersection of meager sets is meager, and the union of countably many meager sets is meager, reflecting the Baire category theorem's emphasis on category rather than measure.
Applications in Mathematics and Analysis
Null sets, characterized by having Lebesgue measure zero, are crucial in real analysis and probability theory for identifying events of negligible size or almost everywhere properties. Meager sets, defined by being countable unions of nowhere dense sets, play a significant role in topology and functional analysis by distinguishing typical or generic properties in Baire category theory. Both concepts are instrumental in ergodic theory, harmonic analysis, and descriptive set theory, where they help classify sets according to measure-theoretic and topological smallness, influencing convergence, continuity, and genericity results.
Summary: Choosing Between Null and Meager Sets
Null sets, defined by having Lebesgue measure zero, are central in measure theory and highlight negligible size in terms of volume, while meager sets, characterized as countable unions of nowhere dense sets, relate to category and topological structure rather than measure. The choice between null and meager sets depends on the mathematical context: null sets are preferred in measure theory and probability for focusing on negligible measure, whereas meager sets are favored in topology and functional analysis for studying generic properties and typical behavior. Understanding the distinction and application of null versus meager sets is crucial for rigorous analysis in real analysis, descriptive set theory, and dynamical systems.
Null set Infographic
 libterm.com
libterm.com