Coinitial is a leading provider of API security solutions designed to protect your digital assets from evolving cyber threats. Their advanced technology ensures seamless integration and real-time threat detection, enhancing your organization's cybersecurity posture without compromising performance. Explore the rest of the article to discover how Coinitial can safeguard your business and improve your security strategy.
Table of Comparison
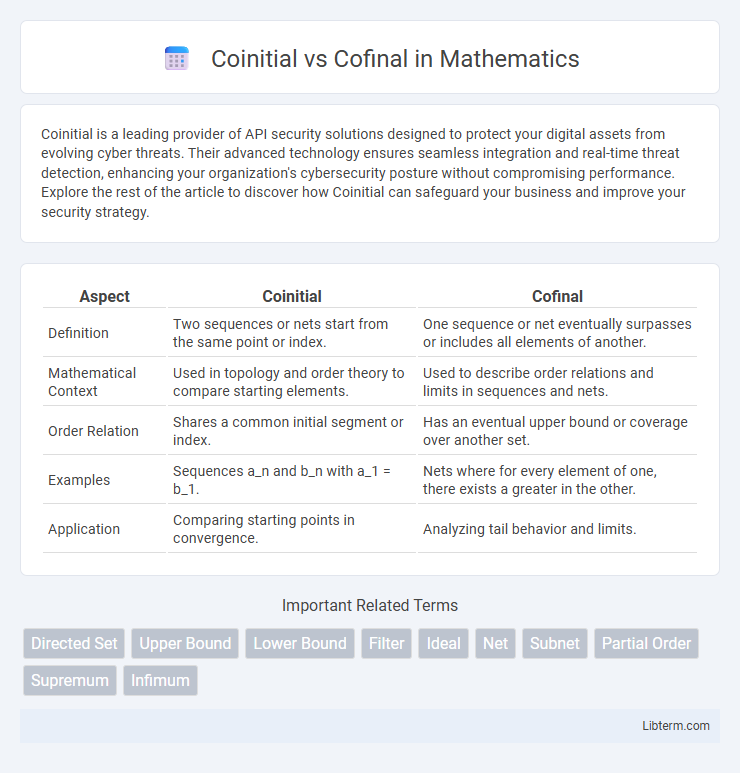
| Aspect | Coinitial | Cofinal |
|---|---|---|
| Definition | Two sequences or nets start from the same point or index. | One sequence or net eventually surpasses or includes all elements of another. |
| Mathematical Context | Used in topology and order theory to compare starting elements. | Used to describe order relations and limits in sequences and nets. |
| Order Relation | Shares a common initial segment or index. | Has an eventual upper bound or coverage over another set. |
| Examples | Sequences a_n and b_n with a_1 = b_1. | Nets where for every element of one, there exists a greater in the other. |
| Application | Comparing starting points in convergence. | Analyzing tail behavior and limits. |
Introduction to Coinitial and Cofinal Concepts
Coinitial and cofinal concepts relate to the ordering of elements within partially ordered sets or sequences. A subset is coinitial in an ordered set if every element in the set has a smaller or equal element in the subset, while a subset is cofinal if every element in the set has a larger or equal element in the subset. These concepts are fundamental in order theory and topology for understanding bounds, limits, and convergence behavior of sequences and nets.
Definitions: Coinitial vs. Cofinal
Coinitial refers to two subsets of a partially ordered set where each element of one subset is greater than or equal to some element of the other, establishing a mutual lower bound relation. Cofinal describes a subset whose elements are always greater than or equal to elements of another subset, ensuring that for every element in the latter, there exists an element in the cofinal subset that is larger or equal. These concepts play a crucial role in order theory, particularly in analyzing directed sets and nets.
Historical Background and Origin
Coinitial and cofinal concepts originate from order theory in mathematics, with roots tracing back to early 20th-century set theory researchers such as Georg Cantor and Felix Hausdorff. Historians highlight that cofinality was formalized to describe the minimal ordinal type of unbounded subsets in partially ordered sets, playing a crucial role in studying infinite cardinalities and their structure. The term coinitial emerged to characterize initial segments in ordered sets, complementing cofinality by focusing on minimal elements and foundational structures in linear orders.
Mathematical Contexts: Order Theory and Beyond
Coinitial and cofinal subsets play crucial roles in order theory, where a coinitial subset of a partially ordered set contains elements that are less than or equal to every element of the larger set, while a cofinal subset includes elements greater than or equal to every element of the set. These concepts extend beyond order theory to areas like lattice theory and topology, influencing the behavior of filters, ideals, and nets. Understanding the interplay between coinitial and cofinal subsets aids in characterizing completeness properties and constructing limits in various mathematical structures.
Key Differences Between Coinitial and Cofinal
Coinitial refers to two or more sequences or sets sharing the same initial element or starting point, while cofinal describes sequences or subsets where one is contained within or extends beyond another towards infinity in ordered structures. The key difference lies in their positional relation: coinitial emphasizes a shared beginning, cofinal emphasizes an eventual overlap or inclusion irrespective of the start. In set theory and order theory, recognizing coinitial subsets helps analyze initial segment behavior, whereas cofinal subsets are crucial for understanding limit points and supremum considerations.
Illustrative Examples and Visualizations
Coinitial segments in order theory refer to subsets containing all elements less than or equal to a certain point, exemplified by intervals like [0, a] in real numbers, visualized as left-closed segments extending from the start of the set up to a given element. Cofinal segments include all elements greater than or equal to a particular point, such as [b, ) in real numbers, depicted as right-closed rays moving towards infinity. Visualizing these concepts on a number line highlights the contrast: coinitial sets are anchored at the beginning and extend to a boundary, while cofinal sets start at a boundary and extend indefinitely toward the upper limit.
Importance in Category Theory
Coinitial and cofinal subcategories play a crucial role in simplifying limits and colimits calculations within category theory, enabling the replacement of complex diagrams with more manageable subdiagrams. A cofinal functor ensures the colimit over a larger category is isomorphic to the colimit over the cofinal subcategory, preserving colimit computations, while a coinitial functor guarantees similar preservation for limits. Understanding these concepts allows mathematicians to leverage subcategory structures for efficient analysis of categorical constructions and universal properties.
Applications in Algebra and Topology
Coinitial and cofinal subsets play crucial roles in algebra and topology by describing ordered structures and limits. In algebra, cofinal subsets help characterize directed systems and filtrations, impacting module theory and homological algebra. Topologically, cofinality influences the study of nets and convergence, essential for understanding compactness and continuity in general spaces.
Common Pitfalls and Misconceptions
Coinitial and cofinal are often confused in order theory, where coinitial refers to sets whose elements are arbitrarily small, and cofinal involves elements arbitrarily large. A common misconception is treating these concepts interchangeably, which can lead to incorrect conclusions about the structure or limits of ordered sets. Understanding that coinitial subsets approach the minimal bounds while cofinal subsets approach maximal bounds is crucial to avoid errors in proofs and applications.
Conclusion and Further Reading
Coinitial sets share a common lower bound, whereas cofinal sets share a common upper bound, essential concepts in order theory and lattice structures. Understanding these properties helps in analyzing directed sets, filters, and nets, which are fundamental in topology and functional analysis. For deeper insights, consult advanced texts like "Introduction to Lattices and Order" by Davey and Priestley or "General Topology" by John L. Kelley.
Coinitial Infographic
 libterm.com
libterm.com