A class group fosters collaboration and communication among students, enhancing learning experiences and promoting academic success. Understanding the dynamics of class groups can help you navigate peer interactions and improve teamwork skills. Explore the rest of the article to discover effective strategies for forming and managing class groups.
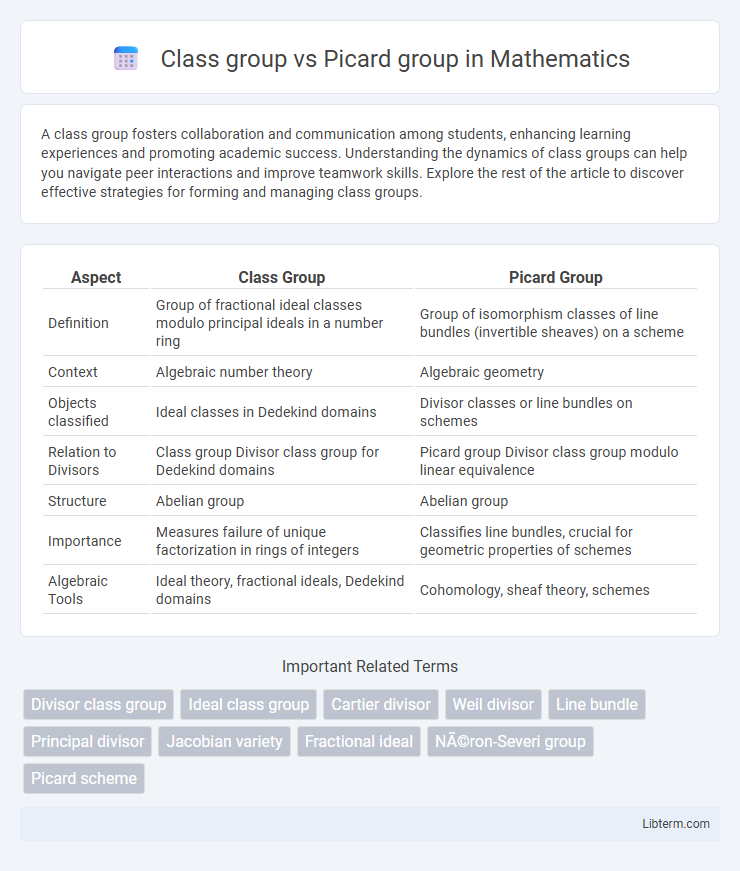
Table of Comparison
| Aspect | Class Group | Picard Group |
|---|---|---|
| Definition | Group of fractional ideal classes modulo principal ideals in a number ring | Group of isomorphism classes of line bundles (invertible sheaves) on a scheme |
| Context | Algebraic number theory | Algebraic geometry |
| Objects classified | Ideal classes in Dedekind domains | Divisor classes or line bundles on schemes |
| Relation to Divisors | Class group Divisor class group for Dedekind domains | Picard group Divisor class group modulo linear equivalence |
| Structure | Abelian group | Abelian group |
| Importance | Measures failure of unique factorization in rings of integers | Classifies line bundles, crucial for geometric properties of schemes |
| Algebraic Tools | Ideal theory, fractional ideals, Dedekind domains | Cohomology, sheaf theory, schemes |
Introduction to Class Group and Picard Group
The Class group measures the failure of unique factorization in the ring of integers of a number field, classifying fractional ideals modulo principal ideals. The Picard group generalizes this concept to algebraic geometry by classifying isomorphism classes of line bundles, or equivalently, invertible sheaves on a variety. Both groups provide essential insights into the arithmetic and geometric structure of algebraic objects through their ideal or line bundle classes.
Historical Development and Motivation
The Class group emerged in algebraic number theory to study unique factorization failures in rings of integers of number fields, capturing ideal equivalence classes to measure this deviation. The Picard group, introduced in algebraic geometry, classifies line bundles or divisor classes on algebraic varieties, generalizing the notion of the class group from number fields to geometric objects. Both concepts evolved to address problems of factorization and divisor equivalence, illustrating deep connections between arithmetic and geometry in modern mathematics.
Definition of the Class Group
The class group of a number field is defined as the quotient of the group of fractional ideals by the subgroup of principal ideals, measuring the failure of unique factorization in the ring of integers. It is a finite abelian group encoding ideal class equivalence, pivotal in algebraic number theory. Unlike the Picard group, which classifies line bundles or divisors up to linear equivalence on algebraic varieties, the class group centers on ideal classes in number fields.
Definition of the Picard Group
The Picard group of a scheme or variety is defined as the group of isomorphism classes of line bundles (or invertible sheaves) equipped with the operation of tensor product. This group captures important geometric information by classifying divisors modulo linear equivalence and generalizing the divisor class group in algebraic geometry. Unlike the class group, which primarily deals with Weil divisors and their equivalence classes, the Picard group emphasizes the role of line bundles and their cohomological properties.
Algebraic Structures: Comparing Class and Picard Groups
Class groups measure the failure of unique factorization in the ring of integers of a number field by classifying fractional ideals modulo principal ideals, forming a finite abelian group. Picard groups generalize this concept to algebraic geometry by classifying line bundles (invertible sheaves) on a scheme, capturing geometric information about divisor classes up to linear equivalence. Both groups serve as fundamental algebraic structures reflecting intrinsic properties of arithmetic and geometric objects through ideal and divisor class representations.
Geometric Interpretations and Examples
The class group of a number field measures the failure of unique factorization in its ring of integers, classifying ideal classes up to principal ideals, while the Picard group of a scheme parametrizes line bundles or invertible sheaves, reflecting geometric divisor classes. In algebraic geometry, the Picard group captures divisors modulo linear equivalence on varieties, corresponding to the group of isomorphism classes of line bundles, exemplified by curves where the Picard group encodes degree and line bundle data. For example, on a smooth projective curve, the Picard group is isomorphic to the divisor class group, whereas in the arithmetic setting, the ideal class group of the ring of integers parallels these notions by classifying fractional ideals modulo principal ideals, connecting algebraic and geometric viewpoints.
Key Differences between Class Group and Picard Group
The Class group of a number field measures the failure of unique factorization in its ring of integers by classifying fractional ideals modulo principal ideals, while the Picard group captures the isomorphism classes of line bundles or divisor classes on an algebraic variety or scheme. The Class group is typically defined in algebraic number theory, focusing on ideal-theoretic properties, whereas the Picard group arises in algebraic geometry, encoding geometric information through Cartier divisors and line bundles. Key differences include their domains of definition--rings of integers versus algebraic varieties--and their interpretations, with the Class group centered on arithmetic ideal theory and the Picard group on geometric divisor theory.
Applications in Algebraic Number Theory
The class group and Picard group both measure the failure of unique factorization, with the class group classifying fractional ideal classes in number fields and the Picard group describing isomorphism classes of line bundles on algebraic varieties. In algebraic number theory, the class group plays a crucial role in understanding the arithmetic of rings of integers, including factorization properties and the distribution of prime ideals. The Picard group's geometric perspective provides powerful tools for studying Diophantine equations, Galois cohomology, and the arithmetic of schemes, bridging number theory with algebraic geometry.
Applications in Algebraic Geometry
Class groups and Picard groups play crucial roles in algebraic geometry by capturing divisorial and line bundle information on algebraic varieties. The class group, defined as the group of Weil divisors modulo linear equivalence, provides insight into the singularity structure and factorization properties of varieties, especially in the study of normal schemes. The Picard group classifies invertible sheaves or line bundles, facilitating the analysis of morphisms, line bundle cohomology, and the construction of moduli spaces, thereby enabling deeper understanding of variety deformations and embedding properties.
Summary and Further Reading
The class group and Picard group are fundamental objects in algebraic number theory and algebraic geometry, respectively, measuring obstructions to unique factorization and line bundle classification. The class group characterizes fractional ideal classes in a number field, while the Picard group classifies isomorphism classes of line bundles on a scheme or variety. For deeper insights, reference "Algebraic Number Theory" by Neukirch and "Hartshorne's Algebraic Geometry" for comprehensive treatments on these groups and their applications.
Class group Infographic
 libterm.com
libterm.com