Associative algebra is a mathematical structure combining elements of algebraic operations and vector spaces, where multiplication is associative, meaning the order of grouping does not affect the outcome. This concept is fundamental in various fields, including abstract algebra, functional analysis, and quantum mechanics, offering a framework for understanding complex systems. Explore the rest of the article to deepen your understanding of associative algebra and its wide-ranging applications.
Table of Comparison
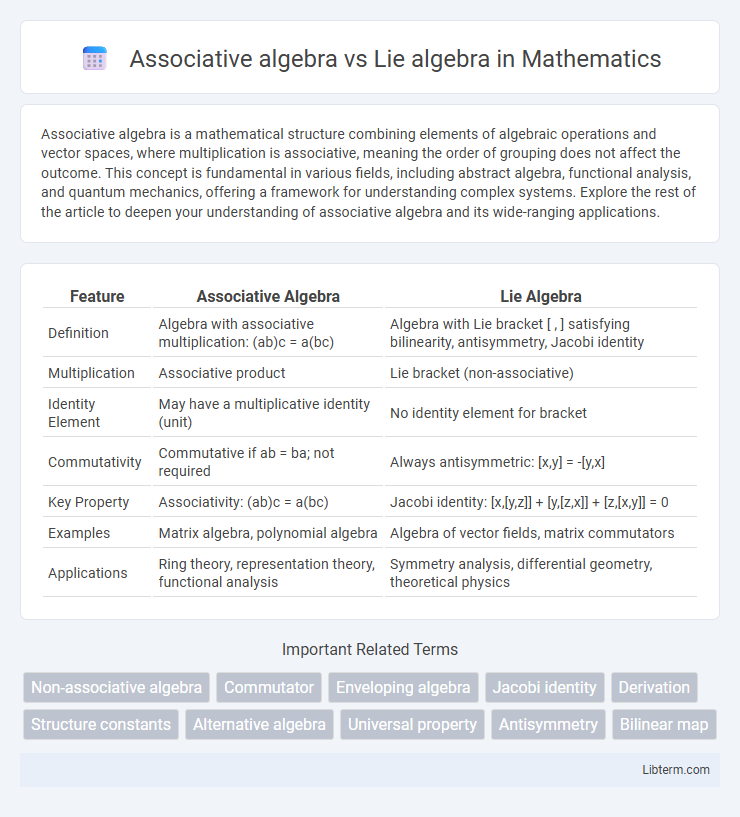
| Feature | Associative Algebra | Lie Algebra |
|---|---|---|
| Definition | Algebra with associative multiplication: (ab)c = a(bc) | Algebra with Lie bracket [ , ] satisfying bilinearity, antisymmetry, Jacobi identity |
| Multiplication | Associative product | Lie bracket (non-associative) |
| Identity Element | May have a multiplicative identity (unit) | No identity element for bracket |
| Commutativity | Commutative if ab = ba; not required | Always antisymmetric: [x,y] = -[y,x] |
| Key Property | Associativity: (ab)c = a(bc) | Jacobi identity: [x,[y,z]] + [y,[z,x]] + [z,[x,y]] = 0 |
| Examples | Matrix algebra, polynomial algebra | Algebra of vector fields, matrix commutators |
| Applications | Ring theory, representation theory, functional analysis | Symmetry analysis, differential geometry, theoretical physics |
Introduction to Algebraic Structures
Associative algebras are algebraic structures equipped with a bilinear, associative multiplication operation, extending concepts of rings and vector spaces, while Lie algebras feature a bilinear, antisymmetric bracket operation satisfying the Jacobi identity representing the algebraic abstraction of infinitesimal transformations. In the context of algebraic structures, associative algebras facilitate the study of modules, representations, and algebraic identities, whereas Lie algebras play a crucial role in describing symmetries and conserved quantities in physics and geometry. Understanding the differences in their defining operations and underlying axioms is fundamental when exploring linear algebraic systems and their applications in advanced mathematical frameworks.
Defining Associative Algebras
Associative algebras are algebraic structures equipped with a bilinear, associative multiplication operation, meaning for elements a, b, c, the equation (ab)c = a(bc) always holds. Unlike Lie algebras, associative algebras emphasize the multiplicative structure mimicking ring-like behavior, where the product is not necessarily anti-commutative or satisfying the Jacobi identity. Key examples include matrix algebras and polynomial algebras, which provide foundational frameworks for representation theory and algebraic geometry.
Understanding Lie Algebras
Lie algebras are algebraic structures characterized by a Lie bracket, a bilinear operation that is antisymmetric and satisfies the Jacobi identity, distinguishing them from associative algebras where multiplication is associative. Understanding Lie algebras involves exploring their role in describing the infinitesimal symmetries of differentiable manifolds and their applications in theoretical physics, particularly in the study of Lie groups and particle physics. Key concepts include the classification of simple Lie algebras, representation theory, and the correspondence between Lie algebras and Lie groups via the exponential map.
Key Differences Between Associative and Lie Algebras
Associative algebras possess a bilinear multiplication that satisfies the associative property, ensuring (ab)c = a(bc) for all elements a, b, c, whereas Lie algebras feature a bilinear Lie bracket operation [a, b] characterized by antisymmetry ([a, b] = -[b, a]) and the Jacobi identity. Associative algebras can be viewed as algebraic structures supporting ring-like multiplication, while Lie algebras are designed to capture the concept of infinitesimal transformations and symmetries in differential geometry and theoretical physics. The key difference lies in the type of multiplication and structural identities each algebra satisfies, impacting their applications and representation theories.
Algebraic Operations: Associativity vs. Lie Bracket
Associative algebras feature a binary operation combining elements that satisfies associativity, meaning (ab)c = a(bc) for any elements a, b, and c, enabling straightforward algebraic manipulations. Lie algebras, in contrast, use the Lie bracket, a bilinear operation that is anti-symmetric and fulfills the Jacobi identity, formalized as [a,[b,c]] + [b,[c,a]] + [c,[a,b]] = 0. This fundamental difference in algebraic operations drives distinct structures and applications, with associative algebras underpinning ring theory and Lie algebras playing a key role in studying symmetries and differential equations.
Examples of Associative Algebras
Examples of associative algebras include matrix algebras, polynomial algebras, and group algebras, each characterized by an associative multiplication operation. Matrix algebras such as M_n(F) consist of nxn matrices over a field F with matrix multiplication that satisfies associativity. Group algebras combine a group G with a field F to form an algebra where the multiplication extends the group operation linearly, maintaining associativity unlike Lie algebras, which rely on a non-associative Lie bracket.
Examples of Lie Algebras
Lie algebras are algebraic structures characterized by a bilinear, antisymmetric bracket operation satisfying the Jacobi identity, commonly exemplified by the algebra of all \( n \times n \) skew-symmetric matrices under the commutator bracket. Another fundamental example is the special linear Lie algebra \(\mathfrak{sl}_n(\mathbb{R})\) consisting of all \( n \times n \) matrices with zero trace, capturing essential symmetries in differential equations and quantum mechanics. These Lie algebras contrast with associative algebras, where the multiplication operation is associative, as in matrix algebra \( M_n(\mathbb{R}) \) with standard matrix multiplication.
Applications in Mathematics and Physics
Associative algebras provide a foundational framework for ring theory and module theory, playing a crucial role in algebraic geometry and representation theory by enabling detailed structural analysis and classification of algebraic objects. Lie algebras, characterized by their anti-commutative Lie bracket, are indispensable in studying symmetries and conservation laws in theoretical physics, particularly in quantum mechanics and gauge theory, where they model the behavior of infinitesimal transformations. Both algebraic structures underpin advanced mathematical physics, with associative algebras often describing observable algebras and Lie algebras governing the dynamics of particle interactions and field theories.
Structural Properties and Representations
Associative algebras are characterized by the associative property of their multiplication operation, enabling the construction of modules that behave like vector spaces with compatible linear maps, while Lie algebras are defined by a bilinear, antisymmetric bracket satisfying the Jacobi identity, leading to representations through Lie algebra modules or actions by derivations. Structural properties of associative algebras include ideals and centers that influence decomposition into simple components, whereas Lie algebras emphasize Cartan subalgebras, root systems, and nilpotent elements to describe their structure. Representation theory for associative algebras often involves module categories and homomorphisms preserving multiplication, contrasted with Lie algebra representations that focus on linear actions compatible with the Lie bracket and use tools like weights and highest weight modules.
Choosing Between Associative and Lie Algebras
Choosing between associative and Lie algebras depends on the algebraic structure and applications involved. Associative algebras feature a binary operation satisfying associativity, making them suitable for modeling matrix algebra and functional analysis, while Lie algebras emphasize the Lie bracket operation, capturing the essence of symmetry and infinitesimal transformations in physics and geometry. Understanding the context, such as representation theory or differential equations, guides the selection of the appropriate algebraic framework.
Associative algebra Infographic
 libterm.com
libterm.com