A simplicial complex is a mathematical structure used to study shapes and spaces through the combination of points, line segments, triangles, and higher-dimensional simplices. This concept plays a crucial role in topology and computational geometry, helping to analyze complex data and spatial relationships. Explore the rest of the article to understand how simplicial complexes can be applied in your fields of interest.
Table of Comparison
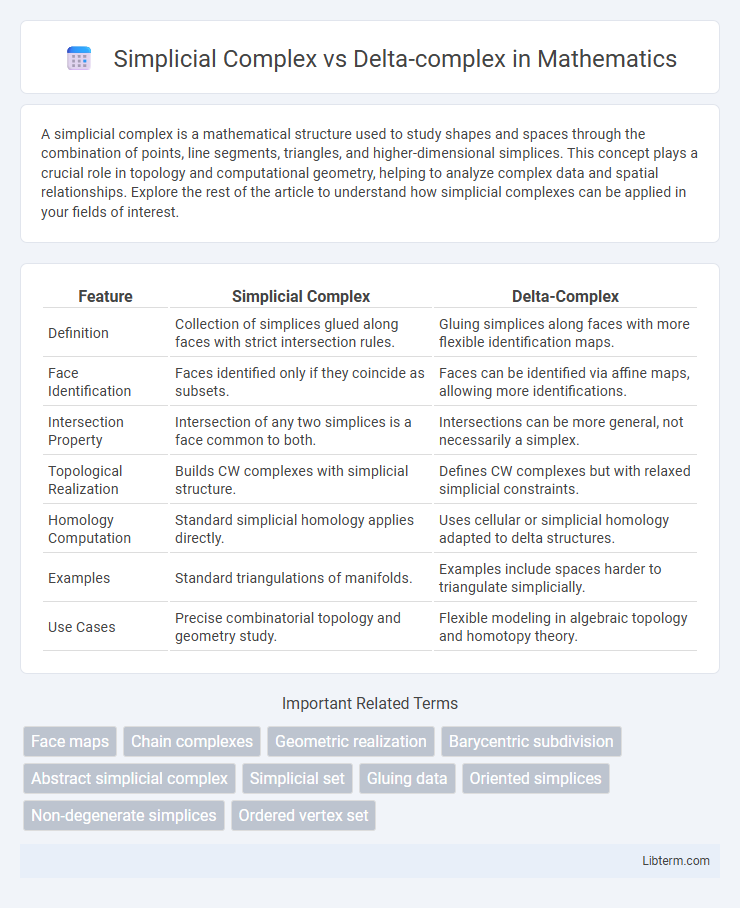
| Feature | Simplicial Complex | Delta-Complex |
|---|---|---|
| Definition | Collection of simplices glued along faces with strict intersection rules. | Gluing simplices along faces with more flexible identification maps. |
| Face Identification | Faces identified only if they coincide as subsets. | Faces can be identified via affine maps, allowing more identifications. |
| Intersection Property | Intersection of any two simplices is a face common to both. | Intersections can be more general, not necessarily a simplex. |
| Topological Realization | Builds CW complexes with simplicial structure. | Defines CW complexes but with relaxed simplicial constraints. |
| Homology Computation | Standard simplicial homology applies directly. | Uses cellular or simplicial homology adapted to delta structures. |
| Examples | Standard triangulations of manifolds. | Examples include spaces harder to triangulate simplicially. |
| Use Cases | Precise combinatorial topology and geometry study. | Flexible modeling in algebraic topology and homotopy theory. |
Introduction to Simplicial Complexes and Delta-complexes
Simplicial complexes are combinatorial structures built from vertices, edges, triangles, and higher-dimensional simplices that fit together in a way satisfying specific face and intersection properties. Delta-complexes generalize simplicial complexes by allowing simplices to be glued together along faces without strict injectivity, enabling more flexible topological constructions. Understanding the foundational definitions highlights that simplicial complexes require unique simplices for each face combination while delta-complexes permit identifications that model spaces with milder combinatorial restrictions.
Historical Background and Mathematical Motivation
Simplicial complexes originated from classical algebraic topology to provide a combinatorial framework for studying topological spaces using simplices glued along faces, formalized in the early 20th century. Delta-complexes, introduced by R.H. Fox and further developed by Eilenberg and Zilber, generalize simplicial complexes by permitting more flexible gluings of simplices, allowing identifications of faces beyond embeddings. This broader framework of delta-complexes arose to better capture homotopy types and to facilitate computations in simplicial sets and CW complexes, bridging combinatorial and algebraic approaches in topology.
Formal Definitions: Simplicial Complex
A simplicial complex is a set of simplices such that every face of a simplex in the complex is also in the complex, and the intersection of any two simplices is either empty or a common face. Formally, a simplicial complex K consists of a collection of simplices {s} satisfying these closure conditions on faces and intersections. This strict combinatorial structure contrasts with delta-complexes, which allow more flexible identifications of simplices but lack the rigid face inclusion property.
Formal Definitions: Delta-complex
A delta-complex is formally defined as a collection of simplices glued together by face maps compatible with the standard simplicial identities, providing a combinatorial structure for topological spaces. Unlike simplicial complexes, delta-complexes allow simplices to share faces without the restrictions of ordering or intersection requirements, enabling more flexible cell attachments. Each n-simplex in a delta-complex is associated with a continuous map from the standard n-simplex, respecting face inclusions, which facilitates the combinatorial analysis of the space's topology.
Key Differences Between Simplicial Complexes and Delta-complexes
Simplicial complexes are collections of simplices glued together along shared faces that must satisfy strict intersection properties, ensuring that any nonempty intersection of two simplices is a single common face. Delta-complexes generalize simplicial complexes by allowing simplices to be glued along faces via arbitrary face maps, which can identify vertices and edges more flexibly, potentially creating overlaps that are forbidden in simplicial complexes. The key difference lies in the intersection conditions and face identifications: simplicial complexes enforce unique gluing along faces without face identifications, whereas delta-complexes permit more general identifications, leading to a richer combinatorial structure.
Examples and Visual Representations
A simplicial complex consists of simplices glued together along shared faces, with examples including triangulations of surfaces like spheres or tori, represented visually by collections of triangles meeting only at vertices, edges, or faces. Delta-complexes, used in algebraic topology, allow more flexible gluings, such as identifying multiple edges from a simplex to form structures like the Klein bottle, visually depicted by polygons with edges labeled and glued in specified patterns. The key difference is that simplicial complexes require strict intersection rules, producing clearer, more rigid visuals, while delta-complexes enable more generalized gluings reflected in their polygonal diagrams with edge identifications.
Topological Properties and Applications
Simplicial complexes provide a combinatorial structure for studying topological spaces through collections of simplices adhering to strict face intersection rules, ensuring strong topological invariants like homology and homotopy types. Delta-complexes relax these conditions by allowing identification of faces in a more flexible manner, enabling easier modeling of geometric structures that are not strictly simplicial but still retain computable topological properties. Applications of simplicial complexes dominate in computational topology and persistent homology, while delta-complexes find use in algebraic topology for simplifying cell decompositions and constructing fundamental groups more intuitively.
Advantages and Limitations of Each Structure
Simplicial complexes offer a straightforward combinatorial structure with well-defined incidence relations, facilitating computations in algebraic topology and ensuring strong geometric realizations, but their rigidity limits modeling more general spaces. Delta-complexes provide greater flexibility by allowing simplices to be glued along faces without strict injectivity conditions, enabling representation of a broader class of topological spaces; however, this flexibility can complicate homological calculations and weaken certain combinatorial properties. The choice between simplicial complexes and delta-complexes depends on balancing computational tractability against the need for modeling complex topologies.
Use Cases in Algebraic Topology
Simplicial complexes are widely used in algebraic topology for their well-defined combinatorial structure, enabling straightforward computation of homology and cohomology groups. Delta-complexes generalize simplicial complexes by allowing simplices to be glued together along faces in a more flexible way, which is advantageous for modeling spaces with singularities or non-manifold features. These structures facilitate the study of topological invariants and enable algorithms for persistent homology in data analysis and computational topology.
Summary and Comparison Table
Simplicial complexes and delta-complexes are both combinatorial structures used to study topological spaces through simplexes, but they differ in their definitions and flexibility. A simplicial complex consists of simplexes joined only along shared faces that are subsets of vertices, ensuring no identification of multiple simplexes along the same face, resulting in a stricter, well-defined geometric realization. In contrast, a delta-complex allows for more general face identifications and multiple gluings along the same simplex, providing greater flexibility in modeling spaces but at the cost of more complex combinatorial data. | Feature | Simplicial Complex | Delta-Complex | |------------------------|------------------------------------|--------------------------------------| | Face identification | Unique face identification | Allows multiple face identifications | | Vertex set definition | Vertices fixed and shared | Vertices form ordered sets in faces | | Geometric realization | Standard simplicial topology | More general, possibly non-regular | | Flexibility | Less flexible, stricter structure | More flexible, richer attachment rules | | Use case | Well-suited for homology and homotopy | Enables modeling of more general cell complexes |
Simplicial Complex Infographic
 libterm.com
libterm.com