Affine transformations preserve points, straight lines, and planes while maintaining parallelism and ratios of distances along parallel lines. This property makes them crucial in computer graphics, image processing, and geometric modeling for scaling, rotating, translating, and skewing objects without distorting their shapes. Explore the rest of the article to understand how affine transformations can enhance your projects and applications.
Table of Comparison
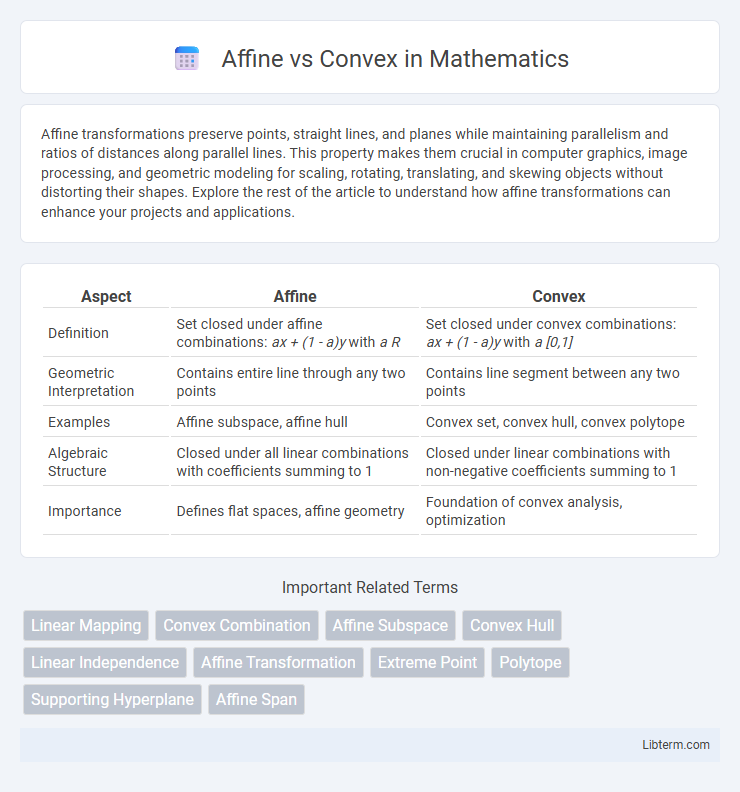
| Aspect | Affine | Convex |
|---|---|---|
| Definition | Set closed under affine combinations: ax + (1 - a)y with a R | Set closed under convex combinations: ax + (1 - a)y with a [0,1] |
| Geometric Interpretation | Contains entire line through any two points | Contains line segment between any two points |
| Examples | Affine subspace, affine hull | Convex set, convex hull, convex polytope |
| Algebraic Structure | Closed under all linear combinations with coefficients summing to 1 | Closed under linear combinations with non-negative coefficients summing to 1 |
| Importance | Defines flat spaces, affine geometry | Foundation of convex analysis, optimization |
Introduction to Affine and Convex Concepts
Affine sets consist of points formed by affine combinations of given points, maintaining linearity without necessarily being convex, whereas convex sets include all convex combinations of points, ensuring every line segment between any two points lies entirely within the set. Affine spaces generalize linear subspaces by allowing translations, while convexity imposes a stricter geometric constraint related to interpolation between points. Understanding the distinction between these concepts is fundamental in optimization, geometry, and linear algebra applications.
Defining Affine Functions and Sets
Affine functions are mappings defined by a linear transformation followed by a translation, expressed as f(x) = Ax + b, where A is a matrix and b is a vector. An affine set contains every affine combination of its points, meaning any weighted sum of its elements where the coefficients sum to one also lies within the set. This contrasts with convex sets, which require that every convex combination, with coefficients non-negative and summing to one, remains within the set, making affine sets broader in scope.
Understanding Convex Functions and Sets
Convex functions are characterized by the property that their epigraphs form convex sets, ensuring that for any two points in the domain, the line segment connecting them lies above or on the graph. Affine functions, a subset of convex functions, have linearity combined with a constant term, making their graphs straight lines or planes that exactly align with any segment between two points in the domain. Understanding convex sets involves recognizing that any linear combination of points within the set, with coefficients summing to one and non-negative, remains inside the set, which is crucial for optimization problems and guaranteeing global minima.
Key Differences Between Affine and Convex Structures
Affine structures represent sets closed under affine combinations, meaning any weighted sum where weights sum to one, allowing for both positive and negative coefficients, while convex structures require non-negative weights summing to one, ensuring all points lie within the "filled-in" region between elements. Affine sets are linear manifolds that can extend infinitely in both directions, whereas convex sets form convex hulls that are always bounded or semi-bounded, containing all line segments between any two points within the set. The key distinction lies in affine sets preserving linear relations without restriction on the sign of coefficients, whereas convex sets restrict combinations to positive coefficients, maintaining the property of convexity essential in optimization problems.
Geometric Interpretation of Affine vs Convex Sets
Affine sets correspond to flat geometric structures such as lines and planes, characterized by the property that any affine combination of points within the set remains inside the set. Convex sets extend this concept by including all points on the straight line segment connecting any two points in the set, resulting in shapes like polygons or ellipsoids that curve inward without indentations. The geometric interpretation distinguishes affine sets as flat subspaces, while convex sets may exhibit curved boundaries but always contain entire line segments between their points.
Mathematical Properties and Theorems
Affine sets are characterized by containing all affine combinations of their points, meaning any linear combination where coefficients sum to one, and they exhibit linearity without curvature. Convex sets include all convex combinations, where the coefficients are non-negative and sum to one, ensuring the set contains all line segments connecting any pair of points within it. Theorems such as the supporting hyperplane theorem apply to both affine and convex sets, but convexity guarantees properties like separation and projection uniqueness, which do not necessarily hold for affine sets.
Applications in Optimization Problems
Affine sets, defined by linear equations and inequalities, play a crucial role in optimization by providing structure to problems involving linear constraints, ensuring feasible regions are flat and predictable. Convex sets, encompassing affine sets as a subset, are fundamental in optimization because they guarantee local minima are global minima, enabling efficient algorithms like gradient descent and interior-point methods. Applications in optimization leverage these properties to solve problems in fields such as machine learning, finance, and engineering design with reliable convergence and solution optimality.
Affine vs Convex in Machine Learning
Affine functions, defined as linear transformations followed by translations, form the basis of many machine learning models by preserving points, straight lines, and planes. Convex functions, characterized by their shape where a line segment between any two points lies above the graph, ensure global minima are attainable through optimization algorithms, crucial for model training. Affine transformations often serve as building blocks in defining convex sets and convex functions, facilitating efficient learning in algorithms such as support vector machines and convex neural networks.
Advantages and Limitations of Each Approach
Affine optimization offers computational efficiency and simpler modeling due to its linear structure, making it suitable for problems where constraints and objectives are linear combinations of variables. Its limitation lies in the inability to handle nonlinearities and non-convexities, which restricts its applicability to more complex real-world scenarios. Convex optimization benefits from guaranteed global optimality and robustness in a broader class of problems, but the increased complexity can lead to higher computational costs and requires more sophisticated algorithms to solve effectively.
Summary and Practical Implications
Affine sets are defined by linear equations and include all points satisfying specific equalities, making them flat and infinitely extending in space. Convex sets contain all line segments connecting any two points within the set, ensuring that weighted averages remain inside, which is crucial for optimization problems. In practice, affine sets simplify constraint representation, while convex sets guarantee global optima in optimization tasks, enhancing solution reliability and computational efficiency.
Affine Infographic
 libterm.com
libterm.com