Trivial tasks may seem insignificant but can impact your productivity and focus throughout the day. Recognizing and managing these minor activities helps in prioritizing what truly matters. Explore the rest of the article to discover effective strategies for handling trivial matters efficiently.
Table of Comparison
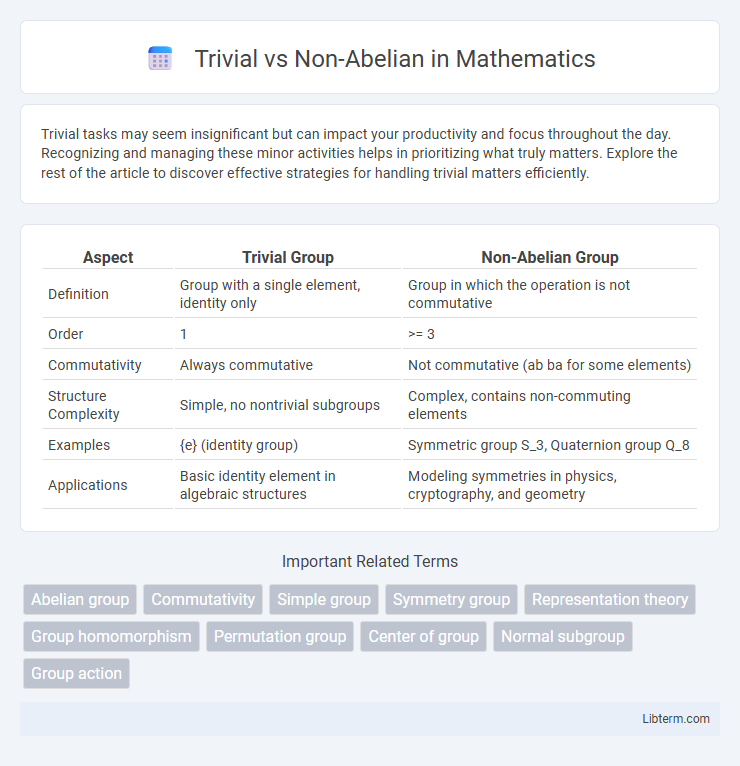
| Aspect | Trivial Group | Non-Abelian Group |
|---|---|---|
| Definition | Group with a single element, identity only | Group in which the operation is not commutative |
| Order | 1 | >= 3 |
| Commutativity | Always commutative | Not commutative (ab ba for some elements) |
| Structure Complexity | Simple, no nontrivial subgroups | Complex, contains non-commuting elements |
| Examples | {e} (identity group) | Symmetric group S_3, Quaternion group Q_8 |
| Applications | Basic identity element in algebraic structures | Modeling symmetries in physics, cryptography, and geometry |
Understanding Trivial and Non-Abelian Concepts
Trivial groups contain only the identity element, representing the simplest algebraic structures with no complexity in operation. Non-Abelian groups have elements whose operations do not commute, meaning the order affects the outcome and introduces richer structural properties. Understanding the distinction between trivial and non-Abelian groups is essential for grasping symmetry, group actions, and their applications in mathematics and physics.
Mathematical Definitions: Trivial vs Non-Abelian
A trivial group in mathematics is defined as a group containing only the identity element, making its operation commutative and structurally simple. Non-Abelian groups are characterized by at least two elements whose operations do not commute, meaning the order of multiplication affects the outcome. This fundamental difference impacts group theory applications, with trivial groups representing the simplest cases and non-Abelian groups modeling more complex symmetries and algebraic structures.
Group Theory: Key Differences
Trivial groups consist of a single element, serving as the identity element, while non-Abelian groups have multiple elements with non-commutative operations. In non-Abelian groups, the order of multiplication affects the outcome, unlike trivial groups where operations are inherently commutative due to the single element. Key examples of non-Abelian groups include symmetric groups \( S_n \) for \( n \geq 3 \), which illustrate complex symmetry structures beyond trivial behavior.
Trivial Groups Explained
Trivial groups consist of a single element where every group operation results in that element, making them the simplest possible groups in abstract algebra. They serve as the identity element in the category of groups and provide a baseline for understanding more complex structures like non-Abelian groups, which feature non-commutative operations. The trivial group's properties highlight fundamental concepts such as closure, associativity, identity, and inverses without introducing complexity from multiple elements or non-commutative operations.
Non-Abelian Groups: An Overview
Non-Abelian groups, characterized by their non-commutative operation where the order of elements affects the result, play a pivotal role in modern algebra and theoretical physics. These groups encompass fundamental structures such as permutation groups and matrix groups, which underpin symmetries in particle physics and quantum mechanics. Their complex algebraic properties enable the modeling of phenomena that trivial, commutative groups cannot capture, highlighting the importance of non-Abelian groups in advanced mathematical frameworks.
Properties of Trivial Structures
Trivial structures possess the defining property of containing a single identity element that commutes with itself, resulting in an abelian group with no nontrivial substructures. Their simplicity ensures that all operations are inherently associative and commutative, leading to straightforward algebraic behavior. In contrast, non-abelian groups exhibit more complex properties such as non-commutative operations and richer subgroup lattices.
Non-Abelian Characteristics and Examples
Non-Abelian groups are characterized by their non-commutative property, meaning the group operation does not satisfy the commutative law (ab ba for some elements a and b). Prominent examples include the symmetric group S_n for n >= 3, which governs permutations, and matrix groups like the special linear group SL(2, R), essential in quantum mechanics and gauge theory. These non-Abelian structures play a critical role in modern mathematics and physics due to their complex symmetry properties and applications in particle interactions and crystallography.
Real-World Applications
Trivial groups, characterized by their single-element structure, serve foundational roles in basic symmetry and identity operations within computer science algorithms and cryptographic primitives. Non-Abelian groups, with complex non-commutative properties, underpin advanced real-world applications such as particle physics symmetry groups in the Standard Model and robotics path planning through Lie groups. The distinction between trivial and non-Abelian structures is critical in quantum computing for designing error-correcting codes and understanding topological quantum states.
Comparing Trivial and Non-Abelian in Algebra
Trivial groups contain only the identity element, exhibiting no nontrivial group operations, whereas non-Abelian groups have elements that do not commute under the group operation, meaning \(ab \neq ba\) for some elements \(a\) and \(b\). In algebra, trivial groups represent the simplest structure with a single element, serving as the identity for group homomorphisms, while non-Abelian groups embody complexity found in symmetry groups such as the dihedral group \(D_n\) and the symmetric group \(S_n\). Comparing trivial and non-Abelian groups highlights the difference in structural properties, where trivial groups are always Abelian, and non-Abelian groups demonstrate rich, non-commutative behavior fundamental to fields like quantum mechanics and crystallography.
Summary: Importance in Mathematics
Trivial groups serve as the fundamental baseline in group theory, representing the simplest structure with only the identity element. Non-Abelian groups exhibit complex properties due to their non-commutative operations, crucial for understanding symmetry in advanced mathematics and theoretical physics. The distinction between trivial and non-Abelian groups is essential for classifying mathematical structures and analyzing algebraic systems.
Trivial Infographic
 libterm.com
libterm.com