Understanding the concept of limits is essential in calculus as it describes the behavior of a function as its input approaches a particular point. Limits help in defining derivatives and integrals, forming the foundation for advanced mathematical analysis. Explore the rest of the article to deepen your understanding of limits and their applications.
Table of Comparison
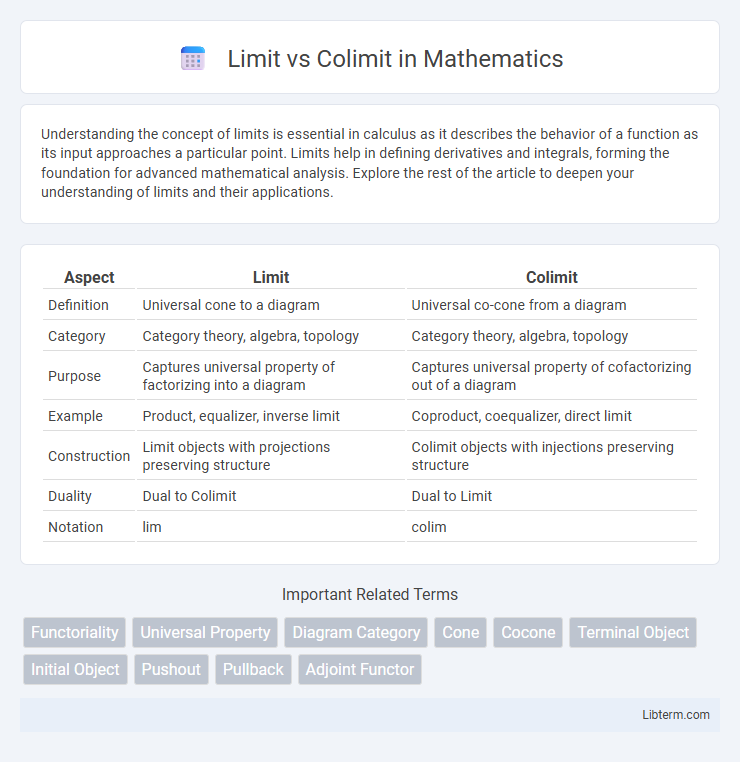
| Aspect | Limit | Colimit |
|---|---|---|
| Definition | Universal cone to a diagram | Universal co-cone from a diagram |
| Category | Category theory, algebra, topology | Category theory, algebra, topology |
| Purpose | Captures universal property of factorizing into a diagram | Captures universal property of cofactorizing out of a diagram |
| Example | Product, equalizer, inverse limit | Coproduct, coequalizer, direct limit |
| Construction | Limit objects with projections preserving structure | Colimit objects with injections preserving structure |
| Duality | Dual to Colimit | Dual to Limit |
| Notation | lim | colim |
Introduction to Limits and Colimits
Limits and colimits are fundamental concepts in category theory used to generalize constructions such as products, coproducts, intersections, and unions. A limit captures the notion of a universal cone to a diagram, representing the most general object mapping into the given diagram consistently, while a colimit is the universal co-cone, representing the most general object receiving maps from that diagram. Understanding limits and colimits enables the abstract formulation of constructions across various mathematical contexts, providing a unified framework for analyzing and comparing different categorical structures.
Fundamental Definitions
Limits in category theory represent universal cones, capturing the notion of a universal construction that factors through all other cones to a given diagram. Colimits, dually, are universal co-cones that generalize constructions like coproducts and pushouts by universally co-factoring through all co-cones from a diagram. Both limits and colimits provide foundational tools for understanding and expressing universal properties and constructions in various mathematical contexts.
Key Differences Between Limits and Colimits
Limits in category theory represent universal cones that capture the notion of a product, pullback, or inverse limit, emphasizing the construction of objects through diagrams converging into a single object. Colimits, conversely, are universal co-cones that generalize concepts like coproducts, pushouts, or direct limits, focusing on the amalgamation of objects via a diagram into a coalesced object. The key difference lies in directionality: limits collect data through natural transformations into an apex object, while colimits distribute data from a base object outwards, reflecting dual constructions.
Universal Properties Explained
Limits and colimits in category theory are defined by their universal properties, where a limit represents a universal cone converging to a diagram, capturing the notion of the "best approximation" from above, while a colimit represents a universal co-cone diverging from a diagram, capturing the "best approximation" from below. The universal property of a limit ensures a unique morphism from any other cone to the limit, making it a terminal object in the category of cones, whereas the universal property of a colimit guarantees a unique morphism from the colimit to any other co-cone, making it an initial object in the category of co-cones. These universal properties provide a precise and highly structured way to characterize constructions like products, pullbacks, coproducts, and pushouts in terms of morphism uniqueness and naturality.
Common Examples of Limits
Common examples of limits in category theory include products, pullbacks, and equalizers, each representing a universal construction that generalizes familiar operations in set theory and algebra. Products correspond to the categorical version of Cartesian products, allowing the combination of objects with projection maps. Pullbacks serve as a universal fibered product, capturing the intersection of morphisms, while equalizers identify objects that equalize parallel morphisms, reflecting solutions to equations within categories.
Common Examples of Colimits
Colimits in category theory often generalize constructions like coproducts, pushouts, and coequalizers, which are vital in algebra and topology. A pushout combines two objects along a shared subobject, modeling gluing processes, while coproducts represent categorical sums or disjoint unions. Important examples include quotients in sets, amalgamated sums in groups, and attaching cells in topological spaces, illustrating the versatility of colimits in various mathematical contexts.
Construction Techniques
Limits and colimits in category theory are constructed using universal properties that characterize objects as optimal solutions to diagrams. Limits are typically realized through products and equalizers, combining cones that factor uniquely through given diagrams, whereas colimits are built using coproducts and coequalizers, merging cocones to serve as universal co-cones. Understanding these constructions enables effective manipulation of objects in categories like sets, topological spaces, or modules, facilitating solutions to complex diagrammatic constraints.
Importance in Category Theory
Limits and colimits are fundamental constructions in category theory that generalize universal properties and provide a framework for defining objects via diagrams. Limits capture the notion of universal cones and represent objects like products and pullbacks, guiding the unification of data coherently. Colimits, dually, describe universal co-cones including coproducts and pushouts, playing a crucial role in the study of cohomology, sheaf theory, and the formulation of adjoint functors.
Real World Applications
Limits and colimits play a crucial role in database theory for schema design and data integration, providing frameworks for unifying data from diverse sources while preserving consistency. In computer science, limits help model state and computation through fixed-point semantics, whereas colimits facilitate the composition of processes and systems in concurrency theory. Applied category theory uses limits and colimits to optimize networks and signal processing, enabling efficient resource allocation and system synthesis in engineering problems.
Summary and Further Reading
Limits and colimits are fundamental concepts in category theory representing universal constructions: limits generalize notions like products and pullbacks, while colimits encompass coproducts and pushouts. They serve as tools for unifying and analyzing structures and diagrams within categories, with limits capturing universal cones and colimits capturing universal co-cones. For deeper exploration, consult "Categories for the Working Mathematician" by Saunders Mac Lane and the online resources at nLab and the Stanford Encyclopedia of Philosophy.
Limit Infographic
 libterm.com
libterm.com