A dense set in mathematics is a subset of a space where every point in the space is either in the set or arbitrarily close to a point in the set, ensuring no isolated gaps exist. Understanding the properties of dense sets is crucial for fields like topology, analysis, and real algebraic geometry. Explore the rest of this article to deepen your grasp of dense sets and their applications in various mathematical contexts.
Table of Comparison
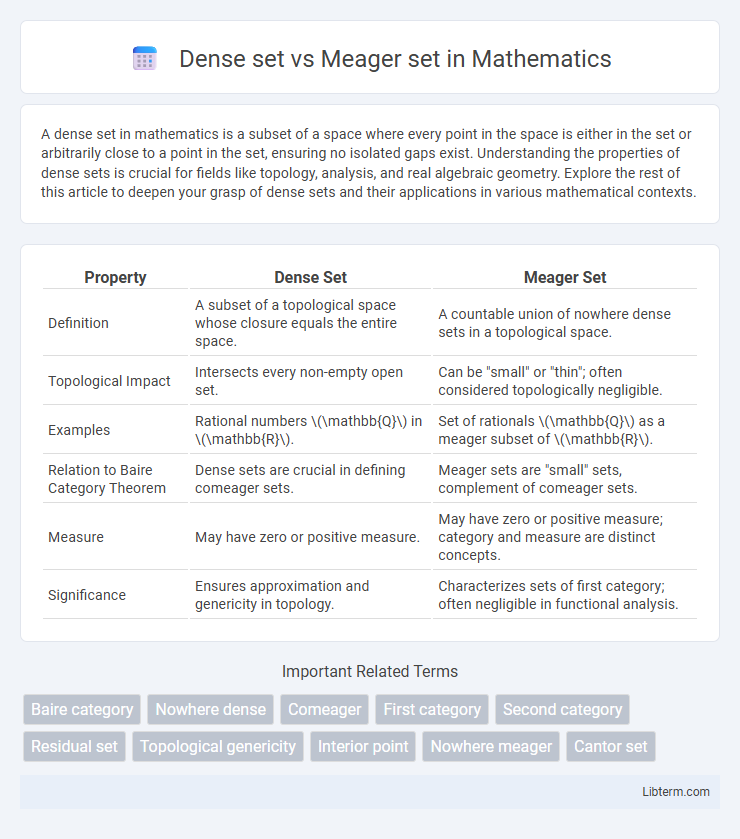
| Property | Dense Set | Meager Set |
|---|---|---|
| Definition | A subset of a topological space whose closure equals the entire space. | A countable union of nowhere dense sets in a topological space. |
| Topological Impact | Intersects every non-empty open set. | Can be "small" or "thin"; often considered topologically negligible. |
| Examples | Rational numbers \(\mathbb{Q}\) in \(\mathbb{R}\). | Set of rationals \(\mathbb{Q}\) as a meager subset of \(\mathbb{R}\). |
| Relation to Baire Category Theorem | Dense sets are crucial in defining comeager sets. | Meager sets are "small" sets, complement of comeager sets. |
| Measure | May have zero or positive measure. | May have zero or positive measure; category and measure are distinct concepts. |
| Significance | Ensures approximation and genericity in topology. | Characterizes sets of first category; often negligible in functional analysis. |
Introduction to Dense and Meager Sets
Dense sets in a topological space are those whose closure is the entire space, meaning they contain points arbitrarily close to every location in the space. Meager sets, also known as sets of first category, are countable unions of nowhere dense sets that do not significantly "fill" the space despite potentially being large in number. Understanding the distinction between dense and meager sets is fundamental in topology and Baire category theory, as dense sets are prevalent while meager sets are considered "small" or negligible.
Formal Definitions
A dense set in a topological space X is a subset A whose closure equals X, meaning every open set in X intersects A. A meager set, also called a set of first category, is a countable union of nowhere dense sets, where each nowhere dense set has an empty interior in X. These formal definitions highlight the contrasting properties: density implies pervasive presence in every open neighborhood, while meagerness reflects a topological smallness or thinness.
Key Differences Between Dense and Meager Sets
A dense set in a topological space is characterized by having its closure equal to the entire space, meaning every open set contains at least one point from the dense set. In contrast, a meager set, also known as a set of the first category, is a countable union of nowhere dense sets and is considered "small" in the sense of Baire category. The key difference lies in their topological size: dense sets are large and pervasive, while meager sets are topologically negligible despite possibly being uncountable.
Examples of Dense Sets in Topology
Examples of dense sets in topology include the set of rational numbers Q within the real numbers R under the standard topology, where every open interval contains infinitely many rationals, making Q dense in R. Another example is the set of algebraic numbers, which is dense in R because every real number can be approximated arbitrarily closely by algebraic numbers. The Cantor set, despite having measure zero, is nowhere dense, contrasting with dense sets that intersect every non-empty open set in a topological space.
Examples of Meager Sets
Examples of meager sets include the rationals within the real numbers, which form a countable union of nowhere dense singletons, and the Cantor set, which is constructed as a perfect nowhere dense set. These sets are "small" in the sense of Baire category despite possibly being dense or uncountable, highlighting their classification as meager or first category sets. Understanding meager sets is crucial in topology and functional analysis, especially when analyzing generic properties and the Baire category theorem.
Properties of Dense Sets
Dense sets in topology are characterized by having their closure equal to the entire space, implying every open set intersects with them. These sets exhibit the property that any point in the space can be approximated arbitrarily closely by elements of the dense set. Unlike meager sets, dense sets are large in the topological sense, ensuring no region of the space is devoid of their presence.
Properties of Meager Sets
Meager sets, also known as sets of first category, are characterized by being countable unions of nowhere dense sets, highlighting their "smallness" in a topological sense despite possibly being dense in a space. These sets have the property that their complement is comeager, meaning the complement is dense and contains a countable intersection of open dense sets. In complete metric spaces, the Baire Category Theorem ensures that meager sets cannot be comeager, emphasizing their negligible size relative to the space they inhabit.
Role in Baire Category Theorem
Dense sets play a crucial role in the Baire Category Theorem by ensuring that the intersection of countably many open dense sets in a complete metric space is dense, which implies the space is not meager. Meager sets, also known as sets of the first category, are characterized as countable unions of nowhere dense sets and represent "small" or topologically negligible subsets. The theorem leverages the distinction between dense and meager sets to establish fundamental properties of completeness and typicality in functional analysis and topology.
Applications in Analysis and Topology
Dense sets are crucial in analysis and topology because they ensure every point in a space can be approximated arbitrarily closely by points from the set, which underpins concepts like continuity, limits, and function approximation. Meager sets, often called sets of the first category, are significant in Baire category theory; they characterize 'small' or 'negligible' sets, helping distinguish generic properties in complete metric spaces. Understanding the interplay between dense and meager sets facilitates proofs in functional analysis, especially within the study of generic properties and residual subsets in topological vector spaces.
Summary and Conclusion
A dense set in a topological space is one whose closure equals the entire space, meaning every open set contains at least one point from the dense set, ensuring its pervasive presence. A meager set, also known as a first category set, is a countable union of nowhere dense sets, representing a "small" or topologically negligible subset. The fundamental distinction lies in their topological size: dense sets are large in terms of coverage, while meager sets are considered sparse or negligible in the Baire category context.
Dense set Infographic
 libterm.com
libterm.com