A cubical set is a mathematical structure used in algebraic topology and category theory to study higher-dimensional shapes and spaces. It consists of collections of cubes of varying dimensions that are connected via face and degeneracy maps, enabling the modeling of complex geometric and topological phenomena. Explore the rest of the article to understand how cubical sets apply to modern mathematics and computational structures.
Table of Comparison
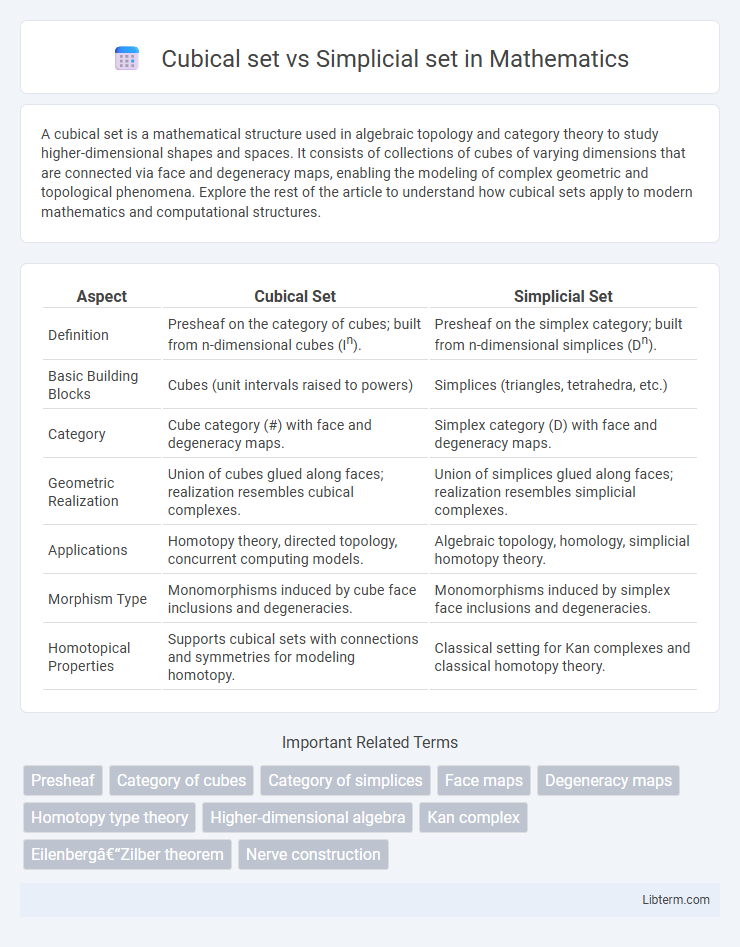
| Aspect | Cubical Set | Simplicial Set |
|---|---|---|
| Definition | Presheaf on the category of cubes; built from n-dimensional cubes (In). | Presheaf on the simplex category; built from n-dimensional simplices (Dn). |
| Basic Building Blocks | Cubes (unit intervals raised to powers) | Simplices (triangles, tetrahedra, etc.) |
| Category | Cube category (#) with face and degeneracy maps. | Simplex category (D) with face and degeneracy maps. |
| Geometric Realization | Union of cubes glued along faces; realization resembles cubical complexes. | Union of simplices glued along faces; realization resembles simplicial complexes. |
| Applications | Homotopy theory, directed topology, concurrent computing models. | Algebraic topology, homology, simplicial homotopy theory. |
| Morphism Type | Monomorphisms induced by cube face inclusions and degeneracies. | Monomorphisms induced by simplex face inclusions and degeneracies. |
| Homotopical Properties | Supports cubical sets with connections and symmetries for modeling homotopy. | Classical setting for Kan complexes and classical homotopy theory. |
Introduction to Cubical and Simplicial Sets
Cubical sets are combinatorial structures built from n-dimensional cubes, providing a framework for modeling higher-dimensional spaces and homotopies through face and degeneracy maps. Simplicial sets, composed of n-simplices connected via face and degeneracy maps, serve as fundamental tools in algebraic topology for representing topological spaces and their homotopy types. Both cubical and simplicial sets enable the study of homotopical and categorical properties, with cubical sets offering advantages in handling connections and symmetries absent in simplicial complexes.
Historical Context and Development
Cubical sets and simplicial sets emerged from category theory and algebraic topology, with simplicial sets developed in the early 20th century by mathematicians like Eilenberg and Zilber to model homotopy types and topological spaces using simplices. Cubical sets gained prominence later, particularly in the 1960s and 1970s, as an alternative combinatorial structure based on cubes, offering advantages in certain computational and homotopical contexts. The development of cubical sets was influenced by efforts to simplify constructions in homotopy theory and provide a more intuitive geometric interpretation compared to simplicial methods.
Defining Simplicial Sets
A simplicial set is a contravariant functor from the simplex category D to the category of sets, capturing geometric shapes via simplices and their face and degeneracy maps. Unlike cubical sets that use cubes as basic building blocks, simplicial sets model spaces using n-dimensional simplices connected through face and degeneracy relations. The combinatorial nature of simplicial sets enables efficient encoding of homotopical and topological information in algebraic topology and category theory.
Defining Cubical Sets
Cubical sets are presheaves on the category of cubes, constructed from objects representing n-dimensional cubes with face and degeneracy maps encoding their geometric structure. Unlike simplicial sets built from simplices, cubical sets use n-cubes as building blocks, which align naturally with concepts in higher category theory and homotopy theory. The defining structure of cubical sets facilitates modeling of concurrent processes and directed spaces due to their inherent product structure and explicit handling of symmetries.
Geometric Realizations: Cubical vs Simplicial
Geometric realizations of cubical sets involve gluing standard cubes along their faces, creating spaces naturally equipped with product-like structures useful in modeling higher-dimensional cubes and transformations. Simplicial sets realize geometric shapes by assembling simplices, resulting in spaces with intrinsic simplicial complex properties fundamental in algebraic topology and homotopy theory. The key distinction lies in the combinatorial building blocks: cubical sets emphasize cube-based constructions facilitating applications in concurrency and directed topology, while simplicial sets rely on simplices suited for classical topological and categorical frameworks.
Comparisons of Categorical Structures
Cubical sets and simplicial sets serve as foundational structures in category theory and algebraic topology, each providing different combinatorial models for spaces. Cubical sets utilize n-dimensional cubes as their building blocks, supporting strict composition laws and enabling a straightforward description of homotopies and higher categorical structures. Simplicial sets, constructed from n-simplices, offer flexible and well-studied frameworks with rich connections to homotopy theory and model categories, allowing for elegant descriptions of higher categorical limits and colimits.
Homotopy Theory in Cubical and Simplicial Settings
Cubical sets and simplicial sets both serve as combinatorial models for spaces in homotopy theory, with simplicial sets traditionally dominating due to their well-established Quillen model structure and extensive use in classical homotopy and higher category theory. Cubical sets offer alternative advantages by incorporating connections and symmetry operations, enabling more flexible and algebraically natural models for homotopy types, particularly in constructive and computational contexts such as Homotopy Type Theory (HoTT). The study of homotopy theory in cubical versus simplicial settings reveals nuanced differences in Kan condition formulations and fibrancy criteria, influencing the development of higher-dimensional algebraic structures and the interpretation of path objects within their respective model categories.
Applications in Topology and Homotopy Type Theory
Cubical sets provide a combinatorial framework well-suited for modeling higher-dimensional structures in homotopy type theory, enabling constructive interpretations of identity types and supporting path-based reasoning. Simplicial sets have been traditionally utilized in algebraic topology to study homotopy types due to their rich geometric intuition and effective handling of simplicial complexes. While simplicial sets excel in classical homotopy theory, cubical sets offer enhanced computational advantages in formalizing homotopy-theoretic constructions within type-theoretic settings.
Advantages and Limitations of Each Approach
Cubical sets offer a natural framework for modeling higher-dimensional cubes, providing intuitive representations for concurrency and homotopy types, with advantages in computational and algorithmic implementations due to their product structure. However, their complexity increases exponentially with dimension, and they may lack some of the elegant combinatorial properties found in simplicial sets. Simplicial sets excel in algebraic topology due to their simplices' well-understood face and degeneracy maps, supporting rich homotopical and categorical structures, but can be less intuitive for modeling certain geometric constructions and may pose challenges in computational contexts.
Future Perspectives and Research Directions
Future research on cubical sets and simplicial sets is poised to deepen their applications in homotopy theory and higher category theory, particularly through enhanced computational models and algorithmic frameworks. Investigations into their comparative algebraic structures and geometric realizations could unlock innovative approaches in type theory and constructive mathematics. Advancements in computational homotopy and applied topology may leverage the unique combinatorial properties of both sets to optimize data analysis and formal verification processes.
Cubical set Infographic
 libterm.com
libterm.com