A saddle point is a critical point on a surface or graph where the curvature changes direction, resembling a saddle shape. It is neither a local maximum nor a minimum but represents a point of equilibrium that can be crucial in optimization and game theory problems. Explore the rest of this article to understand how saddle points influence various scientific and mathematical applications.
Table of Comparison
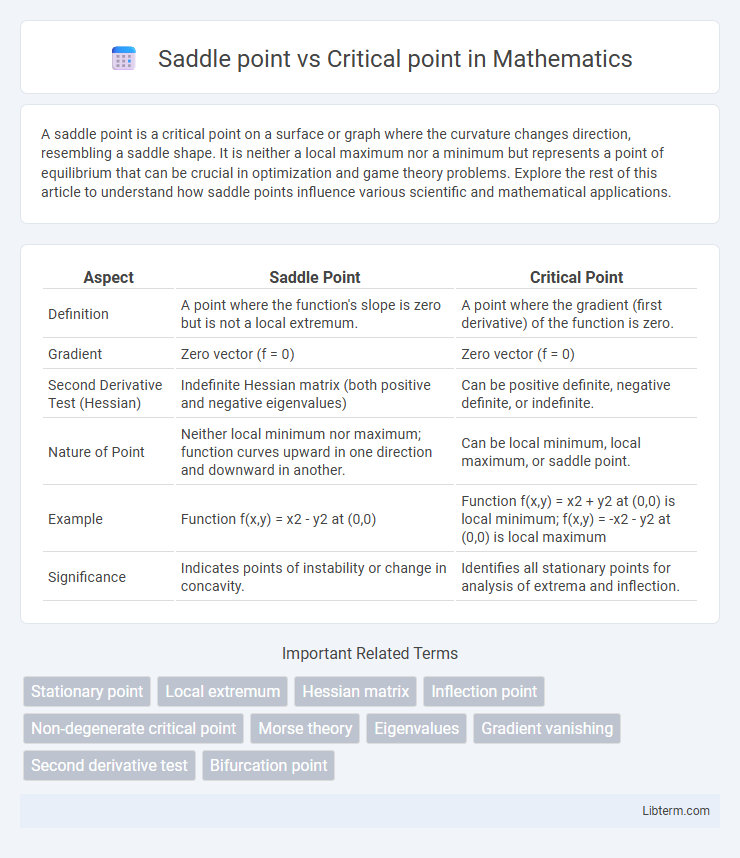
| Aspect | Saddle Point | Critical Point |
|---|---|---|
| Definition | A point where the function's slope is zero but is not a local extremum. | A point where the gradient (first derivative) of the function is zero. |
| Gradient | Zero vector (f = 0) | Zero vector (f = 0) |
| Second Derivative Test (Hessian) | Indefinite Hessian matrix (both positive and negative eigenvalues) | Can be positive definite, negative definite, or indefinite. |
| Nature of Point | Neither local minimum nor maximum; function curves upward in one direction and downward in another. | Can be local minimum, local maximum, or saddle point. |
| Example | Function f(x,y) = x2 - y2 at (0,0) | Function f(x,y) = x2 + y2 at (0,0) is local minimum; f(x,y) = -x2 - y2 at (0,0) is local maximum |
| Significance | Indicates points of instability or change in concavity. | Identifies all stationary points for analysis of extrema and inflection. |
Introduction to Saddle Points and Critical Points
Saddle points are specific types of critical points in multivariable calculus where the function has a stationary value but is neither a local maximum nor a local minimum, often identified by a Hessian matrix with both positive and negative eigenvalues. Critical points occur at locations where the gradient of a function is zero or undefined, representing potential local maxima, minima, or saddle points. Understanding the distinction between saddle and critical points is essential for analyzing function behavior and optimization in higher-dimensional spaces.
Definition of Critical Points in Mathematics
Critical points in mathematics are specific points on a graph where the derivative of a function is zero or undefined, indicating potential locations for local maxima, minima, or saddle points. These points are essential in calculus for identifying where a function's slope changes and determining its behavior. A saddle point, a type of critical point, is characterized by a zero gradient but does not correspond to a local extremum, instead resembling a point of inflection on the surface.
Understanding Saddle Points: Key Concepts
Saddle points are a type of critical point where the first derivative is zero but the second derivative test yields mixed signs, indicating directions of both concave up and concave down curvature. Unlike local maxima or minima, saddle points do not represent extrema but rather points of equilibrium with slope zero in multiple directions. Understanding saddle points is essential in optimization and machine learning, particularly for analyzing the behavior of loss functions and convergence in gradient-based algorithms.
Differences Between Saddle Points and Other Critical Points
Saddle points differ from other critical points such as local maxima and minima by their unique curvature properties, where the Hessian matrix has both positive and negative eigenvalues, indicating directions of ascent and descent. Unlike local extrema, saddle points do not represent a local extreme value but rather a point of equilibrium that is unstable. This distinction is crucial in optimization and multivariable calculus, as saddle points can mislead gradient-based methods and require careful analysis of the Hessian to identify.
Geometric Interpretation of Saddle and Critical Points
A saddle point in a multivariable function is characterized by a surface that curves upwards in one direction and downwards in another, resembling a horse saddle, where the function shows neither a local maximum nor minimum. Critical points occur where the gradient of the function is zero, indicating potential local maxima, minima, or saddle points depending on the Hessian matrix's eigenvalues. Geometrically, saddle points reveal a hyperbolic contour pattern with intersecting concave and convex curvatures, whereas other critical points display purely concave or convex surfaces.
Role in Optimization and Calculus
Saddle points and critical points both occur where the gradient of a function is zero, but their roles in optimization and calculus differ significantly. Critical points include local minima, maxima, and saddle points, with saddle points representing neither maxima nor minima but locations where the function curves upwards in one direction and downwards in another. In optimization, saddle points are crucial because they indicate points of instability and non-optimality, often requiring advanced methods like second-derivative tests or Hessian matrix analysis to distinguish from true extrema.
Examples Illustrating Saddle and Critical Points
In calculus, a saddle point example is the function f(x, y) = x2 - y2, where the surface curves upward in the x-direction and downward in the y-direction, indicating neither a local maximum nor minimum. A critical point example is f(x, y) = x2 + y2, which has a local minimum at (0,0) since the function value increases in every surrounding direction. The distinction lies in the Hessian matrix's eigenvalues: saddle points have both positive and negative eigenvalues, whereas critical points such as minima or maxima have eigenvalues all positive or all negative.
Applications in Machine Learning and Physics
Saddle points in machine learning often represent challenges in optimization algorithms, as gradient-based methods can stall near these points due to zero gradients but non-minimal curvature, affecting convergence in neural network training. Critical points, encompassing minima, maxima, and saddle points, provide essential information about the topology of loss landscapes or potential energy surfaces, thus guiding model parameter tuning and understanding phase transitions in physics. In physics, saddle points correspond to transition states in reaction pathways, critical for calculating activation energy and modeling dynamic systems under equilibrium and non-equilibrium conditions.
Identifying Saddle vs Critical Points in Functions
Saddle points occur where a function's gradient is zero but the Hessian matrix has both positive and negative eigenvalues, indicating a point that is neither a local maximum nor minimum. Critical points are identified by setting the function's first derivatives to zero, and their nature--minimum, maximum, or saddle--is determined by analyzing the Hessian's eigenvalues or definiteness. Functions with positive definite Hessians at critical points correspond to local minima, negative definite to local maxima, and indefinite Hessians indicate saddle points.
Summary: Choosing the Right Terminology
A saddle point is a specific type of critical point where the function's gradient is zero but does not represent a local extremum, showing curvature that changes sign. Critical points encompass all points where the gradient vanishes, including local minima, maxima, and saddle points. Using the term "critical point" is appropriate for general analysis, while "saddle point" precisely describes points exhibiting mixed concavity essential in optimization and dynamical systems.
Saddle point Infographic
 libterm.com
libterm.com