Lagrangian mechanics offers a powerful framework for analyzing the dynamics of physical systems by focusing on energy differences rather than forces. It transforms complex equations of motion into more manageable forms through the use of generalized coordinates, making it essential in fields like classical mechanics, quantum mechanics, and engineering. Discover how understanding the Lagrangian can enhance your grasp of physical phenomena in the rest of this article.
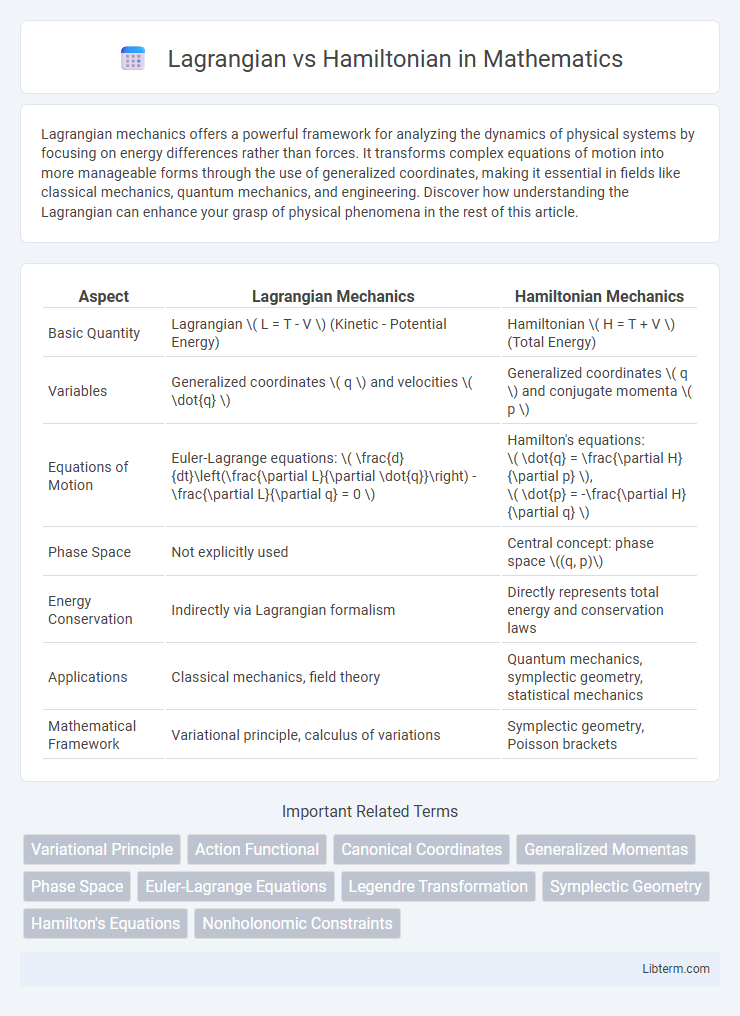
Table of Comparison
| Aspect | Lagrangian Mechanics | Hamiltonian Mechanics |
|---|---|---|
| Basic Quantity | Lagrangian \( L = T - V \) (Kinetic - Potential Energy) | Hamiltonian \( H = T + V \) (Total Energy) |
| Variables | Generalized coordinates \( q \) and velocities \( \dot{q} \) | Generalized coordinates \( q \) and conjugate momenta \( p \) |
| Equations of Motion | Euler-Lagrange equations: \( \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}}\right) - \frac{\partial L}{\partial q} = 0 \) | Hamilton's equations:
\( \dot{q} = \frac{\partial H}{\partial p} \), \( \dot{p} = -\frac{\partial H}{\partial q} \) |
| Phase Space | Not explicitly used | Central concept: phase space \((q, p)\) |
| Energy Conservation | Indirectly via Lagrangian formalism | Directly represents total energy and conservation laws |
| Applications | Classical mechanics, field theory | Quantum mechanics, symplectic geometry, statistical mechanics |
| Mathematical Framework | Variational principle, calculus of variations | Symplectic geometry, Poisson brackets |
Introduction to Lagrangian and Hamiltonian Mechanics
Lagrangian mechanics formulates dynamics through the principle of least action, using the Lagrangian function defined as the difference between kinetic and potential energy (L = T - V). Hamiltonian mechanics reformulates the system in terms of generalized coordinates and conjugate momenta, with the Hamiltonian representing the total energy (H = T + V) of the system. Both approaches are fundamental frameworks in classical mechanics, providing powerful tools for analyzing physical systems and transitions to quantum mechanics.
Historical Development of Analytical Mechanics
The historical development of analytical mechanics began with Joseph-Louis Lagrange's formulation of the Lagrangian mechanics in 1788, which introduced generalized coordinates and the principle of stationary action to simplify the study of dynamic systems. William Rowan Hamilton expanded this framework in the 1830s through Hamiltonian mechanics, creating a powerful reformulation based on canonical coordinates and Hamilton's equations, which laid the groundwork for modern classical and quantum mechanics. These foundational advances transformed the mathematical description of physics by linking variational principles with symplectic geometry and phase space analysis.
Fundamental Concepts: Configuration Space and Phase Space
Lagrangian mechanics describes system dynamics using configuration space, where generalized coordinates represent all possible positions of a system. Hamiltonian mechanics reformulates the problem in phase space, which includes both generalized coordinates and conjugate momenta, offering a complete state representation. This transition from configuration to phase space enables powerful methods in analysis, including symplectic geometry and conservation laws.
The Lagrangian Formalism: Principles and Equations
The Lagrangian formalism is founded on the principle of stationary action, expressing dynamics through the Lagrangian function \( L = T - V \), where \( T \) is kinetic energy and \( V \) is potential energy. The Euler-Lagrange equations, derived from the variational principle, govern the motion: \( \frac{d}{dt} \left( \frac{\partial L}{\partial \dot{q}_i} \right) - \frac{\partial L}{\partial q_i} = 0 \), where \( q_i \) are generalized coordinates. This framework provides a coordinate-independent method to describe conservative systems by focusing on energy differences rather than forces.
The Hamiltonian Approach: Structure and Significance
The Hamiltonian approach reformulates classical mechanics by expressing the system's total energy as a function of generalized coordinates and their conjugate momenta, providing a symplectic structure essential for phase space analysis. This method yields Hamilton's equations, which are first-order differential equations that describe the time evolution of the system more naturally than the second-order Euler-Lagrange equations. The significance of the Hamiltonian framework lies in its pivotal role in bridging classical and quantum mechanics, facilitating canonical quantization and advanced studies in dynamical systems and statistical mechanics.
Comparing Core Equations: Euler-Lagrange vs. Hamilton’s Equations
The Euler-Lagrange equation, derived from the principle of stationary action, governs the dynamics in the Lagrangian formalism by relating generalized coordinates and their velocities through partial derivatives of the Lagrangian function. In contrast, Hamilton's equations transform the problem into a set of first-order differential equations involving generalized coordinates and conjugate momenta, derived from the Hamiltonian function via Legendre transformation. While the Euler-Lagrange equation focuses on minimizing the action integral, Hamilton's equations emphasize the system's evolution in phase space, allowing symplectic structure and conservation laws to be explicitly analyzed.
Advantages of the Lagrangian Method
The Lagrangian method simplifies the analysis of mechanical systems by using generalized coordinates, allowing for easier handling of complex constraints compared to the Hamiltonian approach. It directly applies the principle of least action, enabling the derivation of equations of motion without explicitly computing forces. This method is particularly advantageous in fields like classical mechanics, robotics, and theoretical physics, where coordinate transformations and non-Cartesian systems are common.
Strengths of the Hamiltonian Framework
The Hamiltonian framework excels in offering a clear geometric interpretation of classical mechanics through phase space, facilitating the analysis of conserved quantities and symmetries using Poisson brackets. Its formulation enables straightforward transitions to quantum mechanics via canonical quantization, making it essential for modern theoretical physics. Moreover, the Hamiltonian approach efficiently handles constrained systems and provides powerful tools for studying integrable systems and chaos theory.
Applications in Modern Physics and Engineering
Lagrangian mechanics provides a powerful framework for analyzing complex mechanical systems by focusing on energy differences, making it fundamental in fields like robotics, aerospace engineering, and analytical mechanics for deriving equations of motion. Hamiltonian mechanics, emphasizing phase space and energy conservation, is crucial in quantum mechanics, statistical physics, and advanced control theory, enabling precise system predictions and stability analysis. Both frameworks are essential in modern physics and engineering, with Lagrangian approaches often used in classical and continuum mechanics while Hamiltonian methods dominate in quantum systems and symplectic integration algorithms.
Choosing the Right Formalism: Key Considerations and Summary
Choosing between the Lagrangian and Hamiltonian formalisms depends on the specific problem's nature and desired outcomes, where the Lagrangian framework is typically preferred for systems described by generalized coordinates and velocity-dependent potentials, while the Hamiltonian formalism excels in phase space analysis and quantum mechanics applications. Key considerations include the ease of handling constraints, with Lagrangian mechanics naturally incorporating holonomic constraints, and the Hamiltonian approach providing a systematic procedure for canonical transformations and conservation laws via Poisson brackets. In summary, the Lagrangian formalism offers intuitive geometric insight and variational principles, whereas the Hamiltonian formalism enables powerful analytical techniques for integrability and quantization, guiding the choice based on problem complexity and computational convenience.
Lagrangian Infographic
 libterm.com
libterm.com