The scalar product, also known as the dot product, is a fundamental operation in vector algebra that results in a single number representing the magnitude of one vector projected onto another. Calculating the scalar product involves multiplying corresponding components of two vectors and summing the results, linking geometric and algebraic interpretations. Explore the rest of the article to deepen your understanding of the scalar product's applications and properties.
Table of Comparison
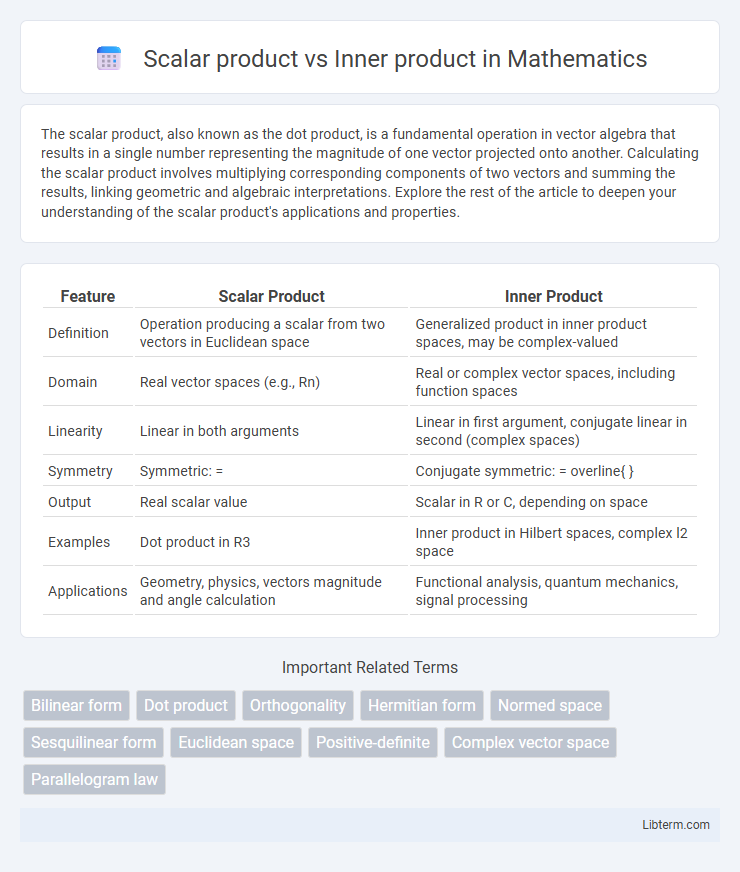
| Feature | Scalar Product | Inner Product |
|---|---|---|
| Definition | Operation producing a scalar from two vectors in Euclidean space | Generalized product in inner product spaces, may be complex-valued |
| Domain | Real vector spaces (e.g., Rn) | Real or complex vector spaces, including function spaces |
| Linearity | Linear in both arguments | Linear in first argument, conjugate linear in second (complex spaces) |
| Symmetry | Symmetric: |
Conjugate symmetric: |
| Output | Real scalar value | Scalar in R or C, depending on space |
| Examples | Dot product in R3 | Inner product in Hilbert spaces, complex l2 space |
| Applications | Geometry, physics, vectors magnitude and angle calculation | Functional analysis, quantum mechanics, signal processing |
Introduction to Scalar Product and Inner Product
The scalar product, also known as the dot product, measures the magnitude of two vectors multiplied component-wise and summed to yield a scalar value, reflecting their directional alignment in Euclidean space. The inner product generalizes this concept to abstract vector spaces, providing a way to define length and angle beyond real coordinate vectors by satisfying linearity, symmetry, and positive-definiteness properties. These products form the foundation for understanding geometric and algebraic relationships in various mathematical and physical applications.
Mathematical Definitions
The scalar product, also known as the dot product, is defined for Euclidean vectors as the sum of the products of their corresponding components, producing a scalar value. The inner product generalizes this concept to abstract vector spaces, satisfying properties of linearity, symmetry (or conjugate symmetry in complex spaces), and positive-definiteness. Unlike the scalar product restricted to finite-dimensional real vectors, inner products apply to complex vector spaces and function spaces, providing a broader framework for measuring angles and lengths.
Historical Background
The scalar product, historically rooted in Euclidean geometry, originated as the dot product used to determine the angle and projection between vectors in three-dimensional space. The concept of the inner product emerged later from abstract algebra and functional analysis, generalizing the scalar product to complex vector spaces and infinite-dimensional Hilbert spaces. Pioneers like Hermann Grassmann and David Hilbert significantly contributed to evolving these ideas from concrete geometric interpretations to abstract mathematical frameworks.
Key Differences Between Scalar Product and Inner Product
The scalar product, commonly known as the dot product, produces a single scalar value by multiplying corresponding components of two vectors and summing the results, primarily defined in Euclidean spaces. The inner product generalizes the scalar product to abstract vector spaces, incorporating properties like linearity, symmetry, and positive-definiteness, enabling the definition of length and angle in more complex contexts. Key differences include the inner product's applicability to complex vector spaces and function spaces, whereas the scalar product is restricted to finite-dimensional real vectors.
Properties and Axioms
The scalar product, often synonymous with the dot product, is a binary operation on vectors in Euclidean space that produces a real number and satisfies properties such as commutativity, distributivity over vector addition, and positive-definiteness. Inner products generalize scalar products to abstract vector spaces, defined by axioms including linearity in the first argument, conjugate symmetry, and positive definiteness, ensuring a complex or real-valued output depending on the field. These axioms guarantee inner product spaces support geometric concepts like length and angle, extending the familiar properties of scalar products beyond Euclidean contexts.
Applications in Physics
The scalar product, also known as the dot product, finds extensive use in classical mechanics for calculating work done by a force and determining projections of vectors. Inner product generalizes this concept in vector spaces, playing a critical role in quantum mechanics where it defines probability amplitudes between quantum states. Both products enable rigorous mathematical modeling of physical phenomena, with the inner product providing a framework for complex vector spaces essential in advanced physics applications.
Applications in Mathematics
The scalar product, commonly known as the dot product, is a specific type of inner product defined in Euclidean spaces used primarily in geometry and physics for calculating projections and angles between vectors. Inner products generalize this concept to abstract vector spaces, enabling the definition of length, orthogonality, and angles in functional analysis and Hilbert spaces. Applications in mathematics include solving differential equations, performing Fourier analysis, and optimizing quadratic forms in linear algebra.
Geometric Interpretations
The scalar product, or dot product, measures the magnitude projection of one vector onto another, resulting in a scalar representing the product of their lengths and the cosine of the angle between them. The inner product generalizes this concept to abstract vector spaces, providing a measure of orthogonality and length through a complex or real-valued function satisfying linearity, symmetry, and positive-definiteness. Geometrically, while the scalar product quantifies angles and lengths in Euclidean space, the inner product extends these geometric interpretations to more abstract spaces, preserving notions of angle and distance.
Common Misconceptions
Scalar product is often mistaken as synonymous with inner product, but while both refer to products of vectors, scalar product is specifically the dot product in Euclidean spaces yielding a scalar, whereas inner product generalizes this concept to abstract vector spaces and may involve complex numbers. A common misconception is that all inner products are commutative; however, inner products in complex vector spaces satisfy conjugate symmetry rather than simple symmetry. Many learners also wrongly assume scalar product always adheres to the Pythagorean theorem, which strictly applies only within Euclidean inner product spaces.
Conclusion and Summary
The scalar product, commonly known as the dot product, is a specific type of inner product defined in Euclidean spaces that produces a single scalar value representing the magnitude of projection between two vectors. Inner products generalize this concept to abstract vector spaces, incorporating additional properties such as linearity, conjugate symmetry, and positive-definiteness, which extend beyond Euclidean geometry. Understanding the distinction highlights that while all scalar products are inner products, not all inner products are scalar products, allowing for broader applications in functional analysis and quantum mechanics.
Scalar product Infographic
 libterm.com
libterm.com