A ring symbolizes commitment, love, and personal style, making it a timeless accessory for any occasion. Whether adorned with precious gems or crafted from sleek metals, rings can convey deep meaning and elevate your fashion statement. Discover the significance and variety of rings to find the perfect one for you in the rest of this article.
Table of Comparison
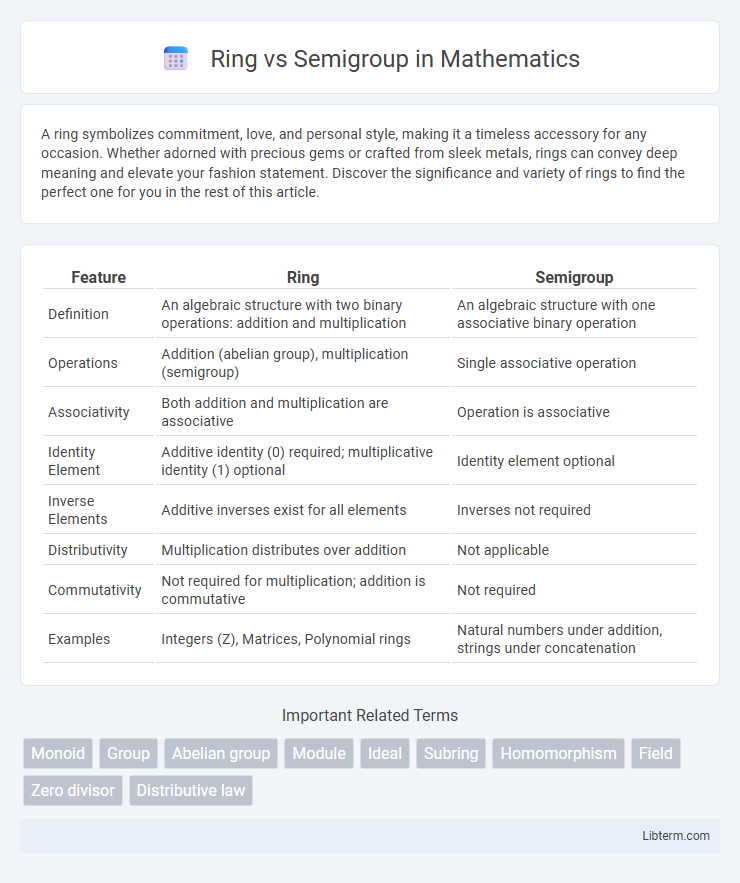
| Feature | Ring | Semigroup |
|---|---|---|
| Definition | An algebraic structure with two binary operations: addition and multiplication | An algebraic structure with one associative binary operation |
| Operations | Addition (abelian group), multiplication (semigroup) | Single associative operation |
| Associativity | Both addition and multiplication are associative | Operation is associative |
| Identity Element | Additive identity (0) required; multiplicative identity (1) optional | Identity element optional |
| Inverse Elements | Additive inverses exist for all elements | Inverses not required |
| Distributivity | Multiplication distributes over addition | Not applicable |
| Commutativity | Not required for multiplication; addition is commutative | Not required |
| Examples | Integers (Z), Matrices, Polynomial rings | Natural numbers under addition, strings under concatenation |
Introduction to Ring and Semigroup
A ring is an algebraic structure consisting of a set equipped with two binary operations: addition and multiplication, where addition forms an abelian group, multiplication is associative, and multiplication distributes over addition. A semigroup is a simpler algebraic structure with a set and a single associative binary operation, lacking requirements for identity or invertibility found in rings. Understanding these foundational differences clarifies the hierarchical relationship and application scope between rings, which model more complex algebraic systems, and semigroups, which capture the essence of associative operations.
Fundamental Concepts: Definitions
A ring is an algebraic structure consisting of a set equipped with two binary operations: addition and multiplication, where addition forms an abelian group, multiplication is associative, and multiplication distributes over addition. A semigroup is a simpler algebraic structure defined by a set with a single associative binary operation, lacking requirements for identity elements or inverses. Rings extend semigroups by incorporating additive identity and inverses, along with distributive laws, making rings fundamental in abstract algebra and number theory.
Key Properties of Semigroups
Semigroups are algebraic structures consisting of a non-empty set equipped with an associative binary operation, lacking the requirements of identity and inverses found in rings. Unlike rings, semigroups do not necessarily possess additive or multiplicative identities, nor do they require the existence of additive inverses. The focus on associativity alone makes semigroups a more general concept, where the binary operation's closure and associative properties are the key defining features.
Key Properties of Rings
Rings are algebraic structures equipped with two binary operations: addition and multiplication, where addition forms an abelian group and multiplication is associative. Unlike semigroups, rings require the existence of additive inverses and distributive laws linking the two operations. Key properties of rings include the existence of a zero element for addition, the presence of additive inverses for all elements, and the distributive property governing multiplication over addition.
Structural Differences Between Rings and Semigroups
Rings are algebraic structures equipped with two binary operations, addition and multiplication, where addition forms an abelian group and multiplication is associative, while semigroups consist of a single associative binary operation without the requirement for additive inverses or identity elements. Unlike semigroups, rings have distributive laws connecting addition and multiplication, ensuring that multiplication distributes over addition from both sides. This structural difference means every ring inherently contains a semigroup under multiplication, but semigroups lack the richer additive framework and distributive properties that characterize rings.
Examples of Semigroups in Algebra
Semigroups in algebra include sets like the natural numbers under addition, where the operation is associative but lacks an identity element, distinguishing them from rings which require both addition and multiplication with additional properties. Another example is the set of all non-empty strings over an alphabet under concatenation, forming a semigroup through associativity without necessarily possessing an additive identity or inverses. These examples highlight semigroups as foundational algebraic structures that generalize groups and rings by relaxing requirements such as the existence of an additive identity or multiplicative inverses.
Examples of Rings in Mathematics
Examples of rings in mathematics include the set of integers \(\mathbb{Z}\) with standard addition and multiplication, which forms a commutative ring with unity. Polynomial rings such as \(\mathbb{R}[x]\), the set of all polynomials with real coefficients, illustrate non-field rings important in algebraic geometry. Matrix rings \(M_n(\mathbb{R})\), consisting of \(n \times n\) real matrices, represent non-commutative rings widely used in linear algebra and functional analysis.
Homomorphisms: Ring vs Semigroup
Ring homomorphisms are structure-preserving maps that respect both addition and multiplication operations, ensuring the image of the additive identity and distributive laws hold. Semigroup homomorphisms, by contrast, only require preservation of the associative binary operation without an additive component or identity element. The richer algebraic structure of rings imposes stricter constraints on homomorphisms compared to semigroups, which affect morphism properties and kernel definitions.
Applications of Rings and Semigroups
Rings are fundamental in algebraic number theory, coding theory, and cryptography due to their structure combining addition and multiplication with distributive properties. Semigroups find applications in computer science, particularly in automata theory, formal languages, and the analysis of state transitions in systems. The versatility of rings supports polynomial factorization and module theory, while semigroups model processes with associative operations without requiring identity elements.
Conclusion: Choosing Between Ring and Semigroup
Choosing between a ring and a semigroup depends on the algebraic structure and operations required for the problem. Rings provide two binary operations (addition and multiplication) with properties such as distributivity and additive inverses, making them suitable for more complex algebraic contexts like module theory or polynomial arithmetic. Semigroups, defined by a single associative binary operation, offer simpler frameworks ideal for studying concatenation processes or partial algebraic systems without the necessity of additive or multiplicative identities.
Ring Infographic
 libterm.com
libterm.com