A finite automaton is a mathematical model used to recognize patterns within input strings by transitioning through a finite number of states. It plays a crucial role in computer science fields like lexical analysis, text processing, and designing digital circuits. Explore the rest of the article to understand how finite automata function and their practical applications in your projects.
Table of Comparison
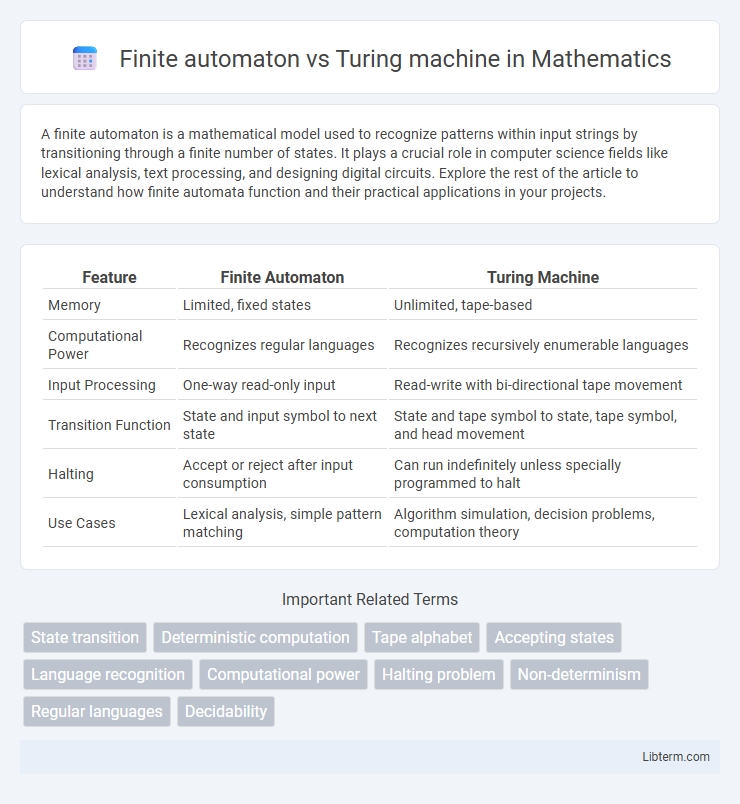
| Feature | Finite Automaton | Turing Machine |
|---|---|---|
| Memory | Limited, fixed states | Unlimited, tape-based |
| Computational Power | Recognizes regular languages | Recognizes recursively enumerable languages |
| Input Processing | One-way read-only input | Read-write with bi-directional tape movement |
| Transition Function | State and input symbol to next state | State and tape symbol to state, tape symbol, and head movement |
| Halting | Accept or reject after input consumption | Can run indefinitely unless specially programmed to halt |
| Use Cases | Lexical analysis, simple pattern matching | Algorithm simulation, decision problems, computation theory |
Introduction to Automata Theory
Finite automata are simple computational models used to recognize regular languages through a finite set of states and transitions, making them ideal for pattern matching and lexical analysis. In contrast, Turing machines, characterized by their infinite tape and read-write capability, provide a more powerful model that can simulate any algorithm, serving as a foundation for defining algorithmic computability. Automata theory explores these computational models, highlighting the limitations of finite automata and the extended capabilities of Turing machines in formal language recognition and decision problems.
What is a Finite Automaton?
A finite automaton is a mathematical model of computation consisting of a finite set of states, transitions between those states, an initial state, and a set of accept states used to recognize patterns or process input strings. It operates on an input tape by reading a single symbol at a time and changing states according to a transition function, making it ideal for regular language recognition and simpler computational tasks. Unlike Turing machines, finite automata have no memory beyond their current state, limiting their computational power to regular languages.
What is a Turing Machine?
A Turing machine is a theoretical computational model capable of simulating any algorithm's logic through an infinite tape divided into cells, a tape head for reading and writing symbols, and a finite set of states controlling its operations. Unlike finite automata, which have limited memory and can only recognize regular languages, Turing machines have unbounded memory, enabling them to recognize a broader class of languages, including recursively enumerable languages. This computational power makes Turing machines fundamental in the study of computability and complexity theory.
Key Differences Between Finite Automata and Turing Machines
Finite automata consist of a finite number of states with transitions based solely on input symbols, lacking the ability to modify or store data beyond their current state. Turing machines feature an infinite tape acting as memory, allowing them to read, write, and move the tape head in both directions, enabling them to simulate any computable function. The computational power of Turing machines surpasses finite automata, as finite automata can only recognize regular languages while Turing machines can decide a broader class of languages including recursively enumerable languages.
Computational Power Comparison
Finite automata have limited computational power, able to recognize only regular languages due to their finite memory and lack of unbounded storage. Turing machines possess greater computational power, capable of simulating any algorithm and recognizing recursively enumerable languages by utilizing an infinite tape as memory. This fundamental difference enables Turing machines to solve a broader range of problems that finite automata cannot address.
Memory and State Management
Finite automata utilize a fixed, finite amount of memory encoded in a limited set of states, restricting their ability to process only regular languages. Turing machines feature an infinite tape serving as unbounded external memory, enabling them to manage complex computations and simulate any algorithm through dynamic state transitions. This fundamental difference in memory capacity and state management makes Turing machines more powerful for recognizing recursively enumerable languages.
Language Recognition Capabilities
Finite automata recognize regular languages by processing input strings through a finite number of states without memory beyond the current state, making them efficient for pattern matching and lexical analysis. Turing machines possess an infinite tape acting as unlimited memory, enabling them to recognize a broader class of languages known as recursively enumerable languages, including context-free and context-sensitive languages. The enhanced computational power of Turing machines allows for solving complex decision problems that finite automata cannot address.
Real-World Applications
Finite automata excel in pattern recognition tasks such as lexical analysis in compilers and network protocol design due to their simplicity and efficiency. Turing machines underpin the theoretical foundation of modern computers, enabling the development of complex algorithms used in artificial intelligence, cryptography, and computational problem solving. While finite automata handle regular languages and simple input processing, Turing machines model general computation necessary for software development and automated reasoning systems.
Limitations of Finite Automata and Turing Machines
Finite automata are limited by their inability to recognize non-regular languages, lacking memory to process nested or recursive patterns, which Turing machines can handle due to their infinite tape and computational power. Turing machines, while more powerful, face practical limitations such as undecidability problems and non-termination in certain computations. The distinction highlights that finite automata are suited for simpler language recognition tasks, whereas Turing machines provide a theoretical foundation for general computation despite inherent theoretical constraints.
Conclusion: Choosing the Right Model
Finite automata are ideal for modeling systems with limited memory and simple state transitions, such as lexical analyzers and pattern matching, due to their efficiency and deterministic behavior. Turing machines provide a more powerful computation model capable of simulating any algorithm, making them essential for understanding computational theory and solving complex decision problems. Selecting the right model depends on the problem's complexity, with finite automata suited for regular languages and Turing machines necessary for context-sensitive or recursively enumerable languages.
Finite automaton Infographic
 libterm.com
libterm.com