Counting measure assigns a value to each subset by counting the number of elements it contains, making it a fundamental concept in measure theory. It is particularly useful in discrete mathematics and probability, where finite or countable sets are involved. Dive deeper into this article to understand how the counting measure operates and its applications in various mathematical fields.
Table of Comparison
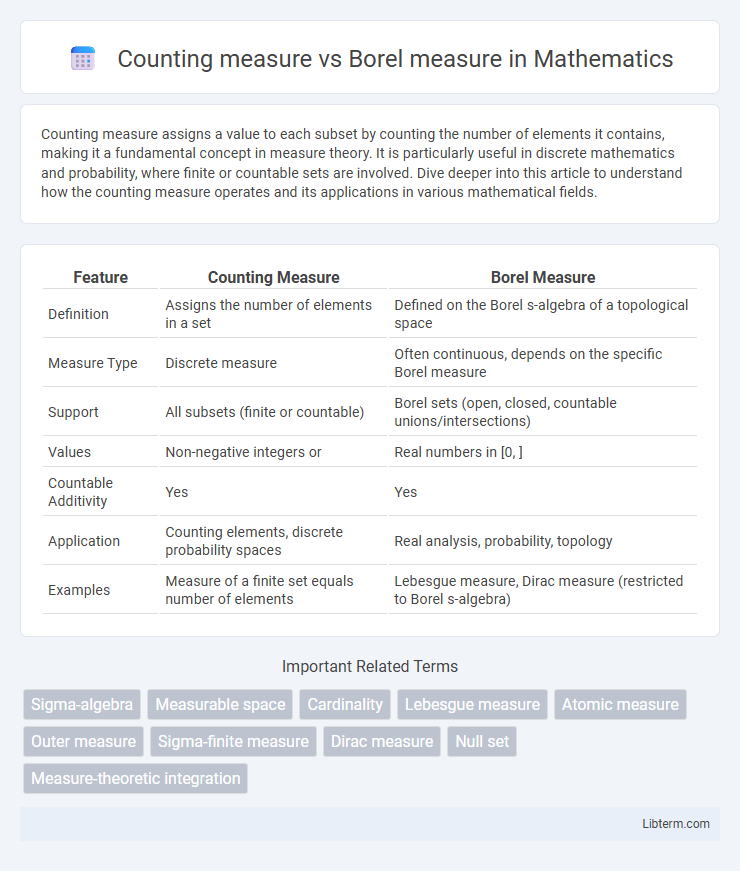
| Feature | Counting Measure | Borel Measure |
|---|---|---|
| Definition | Assigns the number of elements in a set | Defined on the Borel s-algebra of a topological space |
| Measure Type | Discrete measure | Often continuous, depends on the specific Borel measure |
| Support | All subsets (finite or countable) | Borel sets (open, closed, countable unions/intersections) |
| Values | Non-negative integers or | Real numbers in [0, ] |
| Countable Additivity | Yes | Yes |
| Application | Counting elements, discrete probability spaces | Real analysis, probability, topology |
| Examples | Measure of a finite set equals number of elements | Lebesgue measure, Dirac measure (restricted to Borel s-algebra) |
Introduction to Counting Measure and Borel Measure
Counting measure assigns to each subset of a given set the number of elements in that subset, interpreting the measure as the set's cardinality, and is particularly useful in discrete spaces. Borel measure, defined on Borel sigma-algebras generated by open sets in topological spaces like the real line, extends Lebesgue measure and captures sizes of more complex subsets, including intervals and fractals. Both measures serve foundational roles in measure theory, with counting measure primarily for discrete analysis and Borel measure for continuous settings.
Defining Counting Measure
Counting measure assigns to each set the number of elements it contains, providing a straightforward and discrete way to measure subsets of a given set. Unlike Borel measure, which is defined on the s-algebra generated by open sets in a topological space and often relates to length, area, or volume, counting measure is purely cardinal and equates measure with set cardinality. Its simplicity makes counting measure fundamental in discrete measure theory and combinatorial analysis, where measuring finite or countable sets is crucial.
Understanding Borel Measure
Borel measure extends the concept of counting measure by assigning measures to more complex sets beyond countable ones, specifically to Borel sets formed from open or closed sets in a topological space. Unlike counting measure, which only counts elements in discrete sets, Borel measure provides a framework for measuring sizes of subsets in continuous spaces, crucial for probability theory and real analysis. Understanding Borel measure involves grasping how sigma-algebras generated by open sets enable integration and measure on continuous domains, facilitating the study of functions and distributions across real numbers.
Fundamental Differences between Counting and Borel Measures
Counting measure assigns to each subset the number of its elements, making it inherently discrete and atomic, while Borel measure is defined on the s-algebra generated by open sets in a topological space, allowing for more complex, continuous measures. Counting measure is finite on finite sets and infinite on infinite sets, whereas Borel measures can assign finite, infinite, or even zero measure to sets based on their topological properties. The fundamental difference lies in their domains and behavior: counting measure applies to all subsets and reflects cardinality, while Borel measure depends on topology and supports nuanced, measure-theoretic concepts like continuity and outer regularity.
Mathematical Properties of Counting Measure
Counting measure assigns to each set the number of its elements, taking values in the extended non-negative integers, often including infinity for infinite sets. It is a discrete, s-finite measure defined on all subsets of a given set, making it a complete measure that assigns measure zero to the empty set and one to singletons. Unlike Borel measures, which are typically defined on s-algebras generated by open sets in topological spaces, counting measure operates on the power set, emphasizing cardinality rather than geometric or topological properties.
Mathematical Properties of Borel Measure
Borel measure is defined on the sigma-algebra generated by open sets in a topological space, making it central to measure theory and integration on R^n. It is countably additive, regular, and can assign finite measure to compact sets, unlike the counting measure, which assigns measure based solely on cardinality and is sigma-finite only on countable sets. The mathematical properties of Borel measure enable the use of key theorems such as Caratheodory's extension and the Riesz representation theorem, facilitating the link between measures and continuous linear functionals.
Applications of Counting Measure
Counting measure finds extensive applications in discrete mathematics and computer science, particularly in enumerating finite or countable sets such as graphs, networks, and combinatorial structures. It is essential in probability theory on countable sample spaces and analysis of algorithms where integral sums reduce to count measures. Counting measure simplifies measure-theoretic treatment of sequences and discrete random variables, contrasting with Borel measure which applies to continuous spaces and real analysis.
Applications of Borel Measure
Borel measure finds extensive applications in probability theory, functional analysis, and mathematical physics due to its ability to measure sets in topological spaces, particularly on the real line and Euclidean spaces. Unlike the counting measure, which assigns the cardinality of finite sets and is less suited for continuous spaces, Borel measure supports integration over complex geometries and underlies the rigorous formulation of Lebesgue integration. Its role is critical in defining probability distributions, spectral theory, and stochastic processes, where measurable sets correspond to Borel s-algebras generated by open or closed sets.
Examples: Using Counting and Borel Measures
Counting measure assigns to each subset the number of elements it contains, making it ideal for discrete spaces such as the set of integers, where the measure of a finite set is its cardinality. Borel measure extends Lebesgue measure to Borel sets on the real line, useful in continuous contexts like intervals [0,1] where the measure corresponds to length. For example, the counting measure of the set {1, 3, 5} is 3, while the Borel measure of the interval [0,1] is 1.
Comparing Counting Measure vs Borel Measure in Real Analysis
Counting measure assigns to each set the number of elements it contains, making it a discrete measure primarily used on countable sets, whereas Borel measure is defined on the sigma-algebra generated by open sets in a topological space, capturing more complex geometric structures. Counting measure is purely atomic with measure zero for infinite subsets if defined analogously, while Borel measure, such as Lebesgue measure, can assign positive measure to intervals and uncountable sets on the real line. In real analysis, counting measure is useful for summation of series and discrete distributions, while Borel measure underpins integration theory and the study of continuous probability distributions.
Counting measure Infographic
 libterm.com
libterm.com