Sublinear algorithms operate with time or space complexity less than linear, efficiently handling large datasets by processing only a fraction of the input. These algorithms are vital in fields like big data, streaming computations, and property testing, where full data access is costly or impractical. Explore the rest of the article to understand how sublinear methods can optimize Your computational tasks.
Table of Comparison
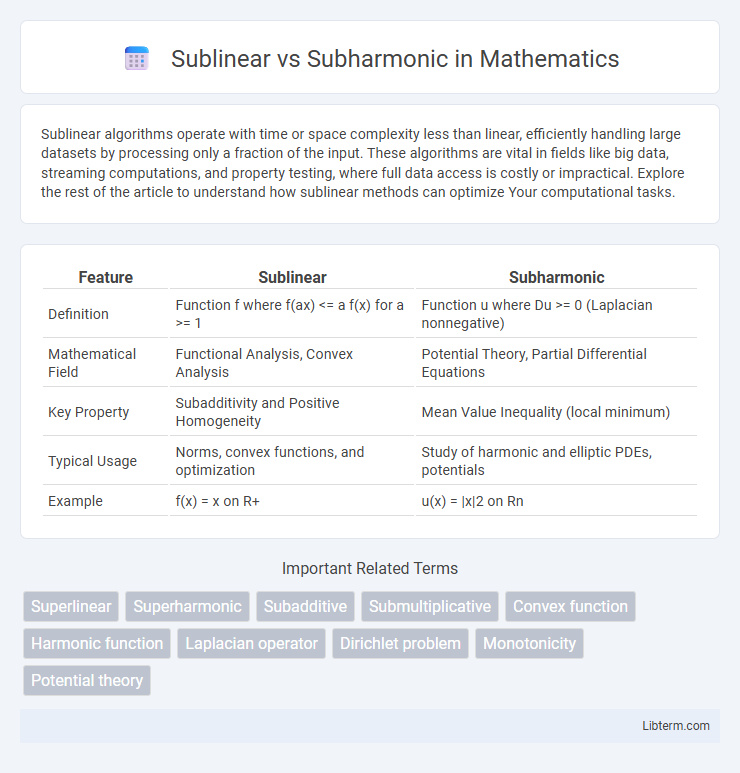
| Feature | Sublinear | Subharmonic |
|---|---|---|
| Definition | Function f where f(ax) <= a f(x) for a >= 1 | Function u where Du >= 0 (Laplacian nonnegative) |
| Mathematical Field | Functional Analysis, Convex Analysis | Potential Theory, Partial Differential Equations |
| Key Property | Subadditivity and Positive Homogeneity | Mean Value Inequality (local minimum) |
| Typical Usage | Norms, convex functions, and optimization | Study of harmonic and elliptic PDEs, potentials |
| Example | f(x) = x on R+ | u(x) = |x|2 on Rn |
Introduction to Sublinear and Subharmonic Concepts
Sublinear operators are mathematical functions exhibiting the property that the operator applied to a sum of inputs does not exceed the sum of the operator applied individually, reflecting a form of controlled growth commonly used in optimization and functional analysis. Subharmonic functions, defined on a domain in complex analysis or potential theory, are upper semi-continuous functions that satisfy the mean value inequality, indicating that their value at any point is less than or equal to the average over surrounding neighborhoods. Understanding these foundational concepts clarifies their roles in various fields such as partial differential equations, harmonic analysis, and convex optimization.
Defining Sublinear Functions
Sublinear functions are characterized by the properties of positive homogeneity and subadditivity, meaning f(ax) = af(x) for a >= 0 and f(x + y) <= f(x) + f(y). Subharmonic functions, in contrast, arise in the context of harmonic analysis and partial differential equations, defined by their mean value property and satisfying Laplace's inequality Du >= 0. The distinction lies in sublinear functions focusing on vector space mappings with linear bounds, while subharmonic functions pertain to scalar-valued functions describing potential theory and complex analysis phenomena.
Understanding Subharmonic Functions
Subharmonic functions are real-valued functions that satisfy the mean value property in an inequality form, meaning the value at any point is less than or equal to the average over any surrounding sphere, making them critical in potential theory and complex analysis. Unlike sublinear functions, which grow slower than a linear function and relate primarily to growth conditions, subharmonic functions are essential in solving partial differential equations, particularly Laplace's equation, by providing tools for maximum principle applications. Understanding subharmonic functions involves studying their behavior under the Laplacian operator, where they are characterized by a nonnegative Laplacian, reflecting their role in describing potential fields and harmonic measure distributions.
Key Differences Between Sublinear and Subharmonic
Sublinear refers to functions or growth rates that increase slower than a linear function, often characterized by exponents between 0 and 1 in mathematical or computational contexts. Subharmonic pertains to frequencies or signals that are integer divisors of a fundamental frequency, typically in physics and engineering, representing oscillations below the base frequency. Key differences lie in sublinear describing a type of growth or function behavior, while subharmonic relates to frequency components in signal analysis and wave phenomena.
Mathematical Properties of Sublinear Functions
Sublinear functions exhibit fundamental mathematical properties including positive homogeneity and subadditivity, which means for any scalars \( \alpha \geq 0 \) and vectors \( x, y \), the function satisfies \( f(\alpha x) = \alpha f(x) \) and \( f(x + y) \leq f(x) + f(y) \). These properties distinguish sublinear functions from subharmonic functions, as subharmonic functions relate primarily to Laplace's equation and potential theory rather than linearity or homogeneity. Sublinear functions are pivotal in convex analysis and optimization, characterizing norms and support functions due to their geometric and functional inequalities.
Mathematical Properties of Subharmonic Functions
Subharmonic functions are characterized by their mean value property, where the value at any point is less than or equal to the average over any surrounding circle, distinguishing them from sublinear functions which primarily concern growth rates relative to a linear function. Mathematically, subharmonic functions satisfy the Laplace inequality Du >= 0, ensuring they cannot possess local maxima unless constant, whereas sublinear functions may not fulfill differential inequalities. The harmonic and subharmonic function framework plays a crucial role in potential theory and complex analysis, underpinning solutions to partial differential equations and conformal mappings.
Applications of Sublinear Functions
Sublinear functions, characterized by positive homogeneity and subadditivity, are essential in optimization, economics, and computational complexity where they model costs and resource constraints efficiently. Their applications include machine learning algorithms for regularization, ensuring scalable performance, and economic theory for utility functions that reflect diminishing returns. Subharmonic functions, related to harmonic analysis and partial differential equations, are primarily used in physics and engineering to describe potential fields and diffusion processes.
Applications of Subharmonic Functions
Subharmonic functions play a crucial role in potential theory, complex analysis, and partial differential equations due to their property of satisfying the mean value inequality, which makes them useful in solving boundary value problems and studying harmonic measures. Applications extend to fluid dynamics, where subharmonic functions model potential flows, and in mathematical physics, they aid in examining the stability of equilibrium states. Their submean properties also facilitate the development of numerical methods for approximating solutions to elliptic PDEs and in optimization problems involving energy minimization.
Common Misconceptions and Clarifications
Sublinear growth describes functions whose rate of increase slows relative to linear functions, while subharmonic functions are solutions to specific partial differential inequalities with a mean value property opposite to superharmonic functions. A common misconception is that "sublinear" and "subharmonic" are interchangeable or related concepts; however, sublinear is a growth condition in analysis, and subharmonic pertains to potential theory in complex analysis and PDEs. Clarification lies in recognizing that sublinear pertains to asymptotic behavior, whereas subharmonic functions are defined through differential inequalities and possess properties useful in harmonic analysis and the theory of elliptic operators.
Summary and Practical Insights
Sublinear and subharmonic functions play key roles in mathematical analysis and potential theory, with sublinear functions growing slower than a linear function, typically satisfying conditions like f(tx) <= t f(x) for 0 <= t <= 1. Subharmonic functions relate to harmonic functions by exhibiting mean value properties that make them instrumental in solving partial differential equations and modeling physical phenomena such as heat distribution and fluid flow. Understanding their differences allows for practical insights in fields like complex analysis, where subharmonic functions help describe boundary behavior of analytic functions, while sublinear growth constraints aid in optimization and control theory applications.
Sublinear Infographic
 libterm.com
libterm.com