Provable security offers a mathematical guarantee that a cryptographic system resists specific types of attacks, ensuring reliability based on well-defined assumptions. This approach helps you understand the strength and limitations of security protocols through rigorous proof models. Explore the rest of the article to uncover how provable security shapes modern cryptography and protects your digital assets.
Table of Comparison
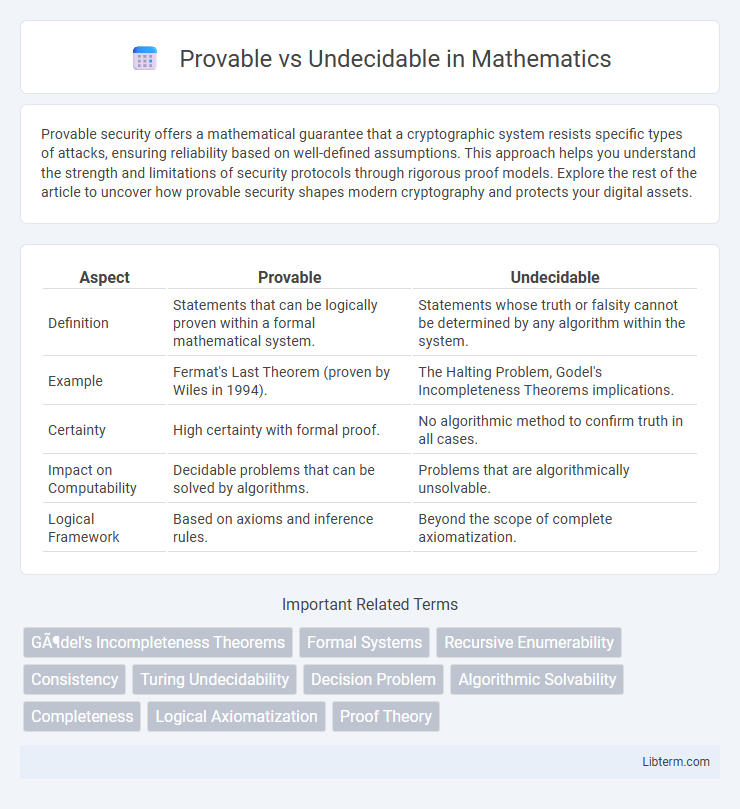
| Aspect | Provable | Undecidable |
|---|---|---|
| Definition | Statements that can be logically proven within a formal mathematical system. | Statements whose truth or falsity cannot be determined by any algorithm within the system. |
| Example | Fermat's Last Theorem (proven by Wiles in 1994). | The Halting Problem, Godel's Incompleteness Theorems implications. |
| Certainty | High certainty with formal proof. | No algorithmic method to confirm truth in all cases. |
| Impact on Computability | Decidable problems that can be solved by algorithms. | Problems that are algorithmically unsolvable. |
| Logical Framework | Based on axioms and inference rules. | Beyond the scope of complete axiomatization. |
Introduction to Provability and Undecidability
Provability concerns the ability to formally prove the truth of a statement within a logical system using a finite sequence of inference rules and axioms. Undecidability refers to problems for which no algorithm can determine, in general, whether statements are provable or true, exemplified by the Halting Problem. Understanding the distinction between provable statements and undecidable problems is fundamental in mathematical logic and theoretical computer science.
Defining Provable Statements
Provable statements are assertions in formal systems that can be demonstrably derived from axioms using a finite sequence of logical inference rules. These statements belong to the class of theorems, where proof procedures verify their truth within a given formal framework, such as first-order logic or Peano arithmetic. Identifying provable statements involves algorithmic methods like proof search or formal deduction, contrasting with undecidable problems where no such algorithmic verification exists.
Understanding Undecidable Statements
Undecidable statements in mathematical logic are propositions for which no algorithm can determine their truth or falsity within a given formal system, distinguishing them from provable statements that have definitive proofs. Understanding undecidable statements involves recognizing limitations of formal systems, as first demonstrated by Godel's incompleteness theorems, which show that some truths cannot be proven or disproven within those systems. This highlights the boundary between algorithms that can verify proofs and problems that remain inherently unsolvable by computational means.
Historical Perspectives on Formal Proof
Historical perspectives on formal proof trace back to Aristotle's syllogistic logic, which laid foundational principles for provability in deductive systems. The 20th century introduced seminal advances with David Hilbert's formalism, advocating for proofs as finite sequences of well-defined statements, contrasted by Kurt Godel's incompleteness theorems, which revealed inherent undecidability within sufficiently complex axiomatic systems. These developments highlight the tension between provable truths encapsulated in formal systems and the presence of undecidable propositions, shaping modern computational logic and mathematical philosophy.
Gödel’s Incompleteness Theorems
Godel's Incompleteness Theorems establish fundamental limits on formal systems by proving that in any sufficiently powerful axiomatic system, there exist true mathematical statements that are undecidable, meaning they cannot be proven or disproven within the system. The first theorem shows the existence of well-formed formulas that are true but not provable, while the second theorem demonstrates that the system cannot prove its own consistency. These results distinguish between provable truths derived through formal proofs and undecidable propositions that evade algorithmic verification, fundamentally impacting logic, mathematics, and computer science.
Key Differences Between Provable and Undecidable
Provable statements are those that can be logically established within a formal system using a finite sequence of axioms and inference rules, ensuring their truth is verifiable. Undecidable propositions are problems or statements for which no algorithm can determine truth or falsehood in all cases, reflecting inherent limits in computational or logical frameworks. The key difference lies in provable statements having conclusive, algorithmically verifiable proofs, whereas undecidable statements resist any general proof or disproof within the system.
Famous Examples of Undecidable Problems
The Halting Problem is a classic example of an undecidable problem, proving that no algorithm can determine whether any arbitrary program halts or runs indefinitely. The Entscheidungsproblem, posed by David Hilbert, is another famous undecidable problem, demonstrating that there is no general algorithm to decide the truth of all mathematical statements in first-order logic. Problems such as Post's Correspondence Problem and the Word Problem for groups also exemplify undecidability in computational theory and algebra.
Implications for Mathematics and Logic
Provable statements in mathematics are those that can be logically derived from a given set of axioms using formal proof systems, ensuring their truth within that framework. Undecidable statements, exemplified by Godel's incompleteness theorems, demonstrate that some propositions cannot be proven or disproven within certain axiomatic systems, revealing inherent limitations in formal logic. This distinction impacts the foundations of mathematics by highlighting that no single formal system can be both complete and consistent, necessitating revised approaches in logic and the philosophy of mathematics.
Approaches to Handling Undecidability
Approaches to handling undecidability include restricting problem domains to decidable subsets, using approximations or heuristics that provide partial solutions, and employing semi-decision procedures that can confirm provability but may not terminate otherwise. Techniques such as bounded model checking and abstraction help manage computational complexity while avoiding undecidable cases. These methods balance practical solvability with theoretical limitations inherent in undecidable problems.
Future Directions in Proof Theory
Future directions in proof theory emphasize developing enhanced automated reasoning tools to address traditionally undecidable problems by integrating machine learning with formal methods. Research is advancing towards creating more expressive formal systems that expand the boundaries of provability while maintaining consistency and computational tractability. Exploration of homotopy type theory and categorical frameworks offers promising avenues for overcoming limitations in classical proof systems and enhancing the understanding of undecidable propositions.
Provable Infographic
 libterm.com
libterm.com