Noether Normalization Lemma establishes that any finitely generated algebra over a field can be expressed as a finite module over a polynomial ring in several variables, providing a foundational tool for understanding algebraic varieties. This lemma simplifies complex algebraic structures by embedding them into a well-understood polynomial ring, which allows you to study their dimension and properties more effectively. Explore the rest of the article to see how Noether Normalization Lemma applies across different areas of algebra and geometry.
Table of Comparison
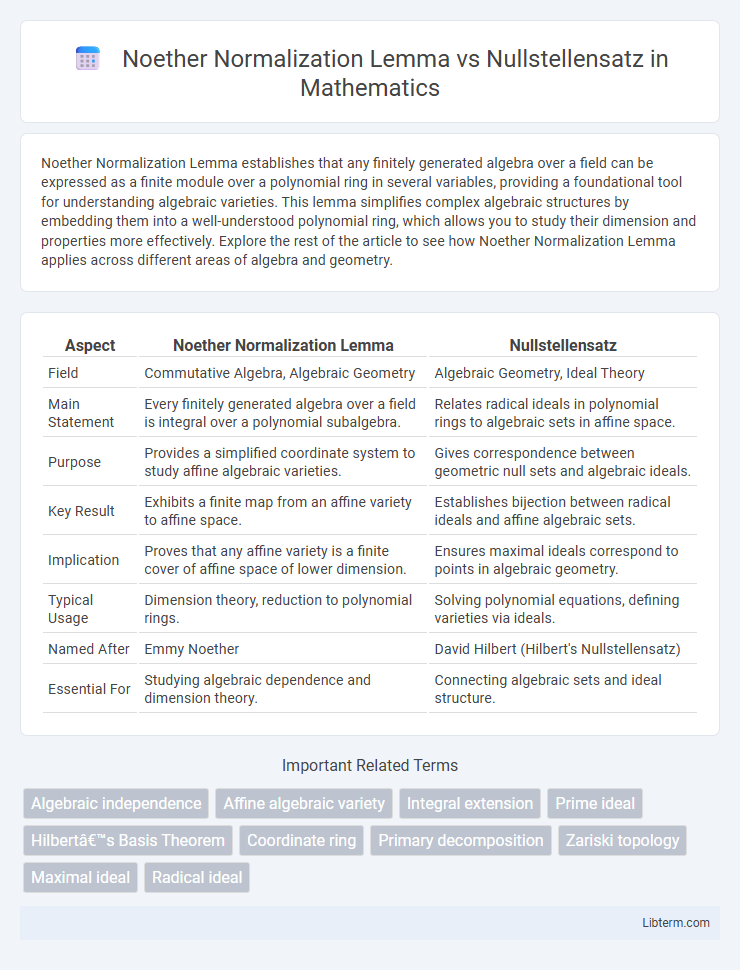
| Aspect | Noether Normalization Lemma | Nullstellensatz |
|---|---|---|
| Field | Commutative Algebra, Algebraic Geometry | Algebraic Geometry, Ideal Theory |
| Main Statement | Every finitely generated algebra over a field is integral over a polynomial subalgebra. | Relates radical ideals in polynomial rings to algebraic sets in affine space. |
| Purpose | Provides a simplified coordinate system to study affine algebraic varieties. | Gives correspondence between geometric null sets and algebraic ideals. |
| Key Result | Exhibits a finite map from an affine variety to affine space. | Establishes bijection between radical ideals and affine algebraic sets. |
| Implication | Proves that any affine variety is a finite cover of affine space of lower dimension. | Ensures maximal ideals correspond to points in algebraic geometry. |
| Typical Usage | Dimension theory, reduction to polynomial rings. | Solving polynomial equations, defining varieties via ideals. |
| Named After | Emmy Noether | David Hilbert (Hilbert's Nullstellensatz) |
| Essential For | Studying algebraic dependence and dimension theory. | Connecting algebraic sets and ideal structure. |
Introduction to Noether Normalization Lemma and Nullstellensatz
Noether Normalization Lemma establishes that any finitely generated algebra over a field can be seen as a finite module over a polynomial ring, providing a foundation for understanding algebraic varieties via simpler coordinate systems. Hilbert's Nullstellensatz connects algebraic geometry and commutative algebra by relating ideals in polynomial rings to the geometric set of their common zeroes, characterizing the radical ideals corresponding to algebraic sets. Together, these theorems form essential tools for translating between algebraic properties of rings and geometric properties of varieties in algebraic geometry.
Historical Background and Mathematical Context
Noether Normalization Lemma, introduced by Emmy Noether in the early 20th century, provides a foundational tool in commutative algebra by establishing a finite morphism from a finitely generated algebra over a field to a polynomial ring, simplifying the study of algebraic varieties. Hilbert's Nullstellensatz, formulated by David Hilbert in 1893, serves as a cornerstone in algebraic geometry by linking ideals in polynomial rings with their zero sets, bridging algebra and geometry. Both results emerged during the development of abstract algebra and geometric methods, with Noether's work focusing on algebraic structure regularity and Hilbert's on the underlying geometric interpretation of polynomial equations.
Core Statements of Noether Normalization Lemma
Noether Normalization Lemma states that for any finitely generated algebra over a field, there exists a polynomial subalgebra over which the algebra is a finitely generated module, effectively providing a way to embed algebraic varieties into affine space of minimal dimension. This lemma is foundational in algebraic geometry, enabling dimensional analysis and simplification of algebraic sets. In contrast, the Nullstellensatz connects ideals in polynomial rings to algebraic sets by characterizing maximal ideals and zeros common to polynomial systems, offering geometric interpretations of algebraic structures.
Fundamental Concepts in Hilbert’s Nullstellensatz
Hilbert's Nullstellensatz establishes a crucial connection between ideals in polynomial rings over algebraically closed fields and the geometry of their zero sets, fundamentally linking algebraic sets to radical ideals. Noether Normalization Lemma provides a structural simplification by mapping a finitely generated algebra over a field onto a polynomial ring, enabling dimension theory and integrality analysis. While Noether Normalization focuses on embedding and dimension reduction of algebraic varieties, Nullstellensatz characterizes the correspondence between varieties and ideals, forming the foundation of algebraic geometry's coordinate ring theory.
Geometric and Algebraic Interpretations
Noether Normalization Lemma provides a constructive method to embed any finitely generated algebra over a field into a polynomial ring, establishing a geometric representation of algebraic varieties as finite covers of affine space, which facilitates dimension theory and simplifies complex varieties. Hilbert's Nullstellensatz connects ideals in polynomial rings with algebraic sets, offering a powerful algebraic characterization of varieties by relating radical ideals to geometric zero loci, thus linking algebraic properties to geometric points. Together, Noether Normalization aids in understanding variety structure through normalization and dimension reduction, while Nullstellensatz ensures a precise algebra-geometry correspondence fundamental to algebraic geometry.
Comparison of Underlying Assumptions
Noether Normalization Lemma assumes a finitely generated k-algebra over a field k, providing a way to embed it into a polynomial ring, highlighting the algebraic structure's dimensionality. Nullstellensatz, particularly Hilbert's Nullstellensatz, relies on algebraically closed fields, establishing a correspondence between ideals in polynomial rings and algebraic sets, emphasizing geometric interpretation. The lemma primarily deals with algebraic independence and normalization, whereas Nullstellensatz bridges ideal theory and geometry through its assumptions of the field's closure properties.
Key Applications in Algebraic Geometry
Noether Normalization Lemma provides a foundational tool for embedding any finitely generated algebra over a field into a polynomial ring, enabling dimension theory analysis in algebraic geometry. Hilbert's Nullstellensatz establishes a direct correspondence between radical ideals in polynomial rings and algebraic sets, crucial for solving systems of polynomial equations and understanding varieties. Together, these theorems underpin the study of algebraic varieties, with Noether Normalization simplifying structural complexity and Nullstellensatz linking geometric objects to algebraic ideals.
Interconnections and Differences Between the Lemmas
Noether Normalization Lemma establishes a foundational algebraic framework by embedding a finitely generated algebra over a field into a polynomial ring, providing a way to study algebraic varieties via coordinate projection. Nullstellensatz characterizes the relationship between ideals in polynomial rings and their common zeros in algebraic geometry, linking algebraic sets with radical ideals. The key interconnection lies in how Noether Normalization simplifies the structure of algebras for applying Nullstellensatz effectively, yet they differ as Normalization is a structural embedding result, whereas Nullstellensatz is a fundamental correspondence between algebraic and geometric objects.
Examples Illustrating Each Theorem
Noether Normalization Lemma guarantees that any finitely generated algebra over a field k can be embedded as a finite module over a polynomial ring k[x_1, ..., x_d]. For example, the coordinate ring k[x,y]/(y^2 - x^3 - x) of an elliptic curve is finite over k[x], illustrating the lemma's role in dimension reduction. Hilbert's Nullstellensatz connects algebraic sets and ideals, showing that for an ideal I in k[x_1, ..., x_n], the radical of I equals the set of all polynomials vanishing on the zero locus of I; for instance, the ideal (x^2 + y^2 - 1) corresponds to the unit circle, and the Nullstellensatz guarantees identifying polynomials vanishing precisely on that circle.
Impact on Modern Algebraic Research
Noether Normalization Lemma provides a structural framework enabling the simplification of affine algebraic varieties by embedding them into polynomial rings, which is fundamental for computational techniques and dimension theory in algebraic geometry. Nullstellensatz establishes a deep correspondence between ideals in polynomial rings and algebraic sets, critical for translating geometric problems into algebraic ones and proving foundational results in algebraic geometry and commutative algebra. Their combined impact drives advancements in algorithmic algebra, invariant theory, and the classification of algebraic varieties, shaping modern research in algebraic structures and geometric intuition.
Noether Normalization Lemma Infographic
 libterm.com
libterm.com