Contravariance is a concept in type theory and programming that allows a function to accept arguments of a more general type than originally specified, enabling greater flexibility in type hierarchies. Understanding how contravariance influences method parameters and delegate compatibility can optimize your code design for better maintainability and reusability. Discover how contravariance can enhance your programming approach by reading the rest of the article.
Table of Comparison
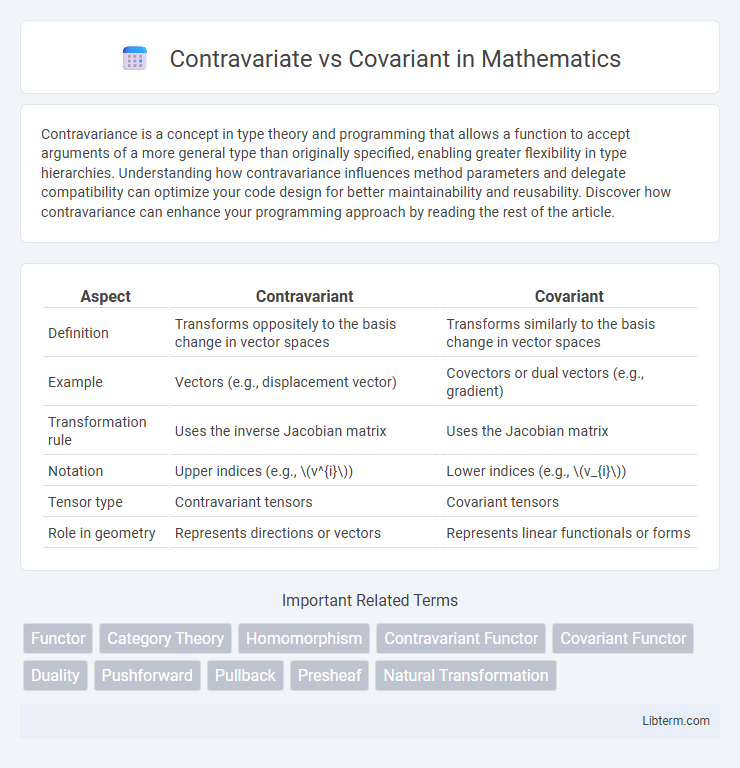
| Aspect | Contravariant | Covariant |
|---|---|---|
| Definition | Transforms oppositely to the basis change in vector spaces | Transforms similarly to the basis change in vector spaces |
| Example | Vectors (e.g., displacement vector) | Covectors or dual vectors (e.g., gradient) |
| Transformation rule | Uses the inverse Jacobian matrix | Uses the Jacobian matrix |
| Notation | Upper indices (e.g., \(v^{i}\)) | Lower indices (e.g., \(v_{i}\)) |
| Tensor type | Contravariant tensors | Covariant tensors |
| Role in geometry | Represents directions or vectors | Represents linear functionals or forms |
Introduction to Contravariate and Covariant Concepts
Contravariant and covariant concepts relate to how types behave in relation to subtyping in type systems. Covariant types preserve the order of subtyping, meaning if type A is a subtype of type B, then a covariant container of A is a subtype of a covariant container of B. Contravariant types reverse this order, where a contravariant container of B is a subtype of a contravariant container of A when A is a subtype of B.
Defining Contravariance and Covariance
Covariance refers to the ability of a type system to preserve the ordering of types when substituting more derived types for base types, commonly seen in output type positions like return values. Contravariance, on the other hand, allows substituting less derived types for more derived ones, usually applicable in input type positions such as method parameters. Understanding the distinction between covariance and contravariance is crucial for safe and flexible type conversions in programming languages supporting generics and polymorphism.
Mathematical Foundations of Variance
Contravariant and covariant concepts arise from category theory and tensor calculus, reflecting how objects transform under mappings with variance indicating the direction of transformation. Covariant entities transform in the same direction as the basis change, aligning with vectors and tensors with lower indices, while contravariant entities transform oppositely, corresponding to dual vectors or tensors with upper indices. Understanding these variances is fundamental in differential geometry and linear algebra, enabling precise manipulation of coordinate-dependent objects and preserving mathematical invariants.
Real-World Examples of Contravariant and Covariant Relationships
In programming, contravariant relationships are exemplified by function parameter types where a method accepting a broader type, such as an Animal, can replace one expecting a narrower type, like Dog, allowing flexibility in input handling. Covariant relationships appear in return types, where a method returning a more specific type, like a Dog, can override one returning a more general type, such as Animal, enabling precise output without breaking compatibility. These principles apply beyond programming, seen in supply chain management where input materials (contravariant) accommodate various sources, while outputs (covariant) specialize in product types tailored to customer needs.
Contravariance and Covariance in Programming
Contravariance and covariance in programming describe how subtyping between more complex types relates to subtyping between their component types. Covariance allows a function to return a more derived type than specified by the original function signature, primarily used in output scenarios such as return types in methods or read-only collections. Contravariance enables a function to accept arguments of less derived types, commonly applied in input parameters of delegates or function arguments, facilitating flexible assignment compatibility in type hierarchies.
Variance in Category Theory and Mathematics
Covariant and contravariant functors describe how morphisms between objects in one category relate to morphisms in another, with covariance preserving the direction of arrows and contravariance reversing it. Variance in category theory formalizes this distinction by defining how functors react to composition and identity morphisms, essential for understanding natural transformations and adjunctions. In mathematical contexts, particularly in type theory and algebra, covariance and contravariance govern the behavior of function types and subtyping relations, crucial for ensuring soundness in type systems and categorical constructions.
Practical Applications in Data Science and Physics
Covariant and contravariant concepts play crucial roles in data science and physics by guiding how variables transform under coordinate changes. In physics, tensors use covariant indices to represent components that transform with the basis, while contravariant indices transform oppositely, essential for defining physical laws invariant under coordinate transformations. In data science, understanding covariance matrices aids in principal component analysis (PCA) for dimensionality reduction, while contravariant transformations underpin gradient computations in optimization algorithms.
Key Differences Between Contravariant and Covariant
Contravariant types reverse the direction of type inheritance, meaning if type A is a subtype of B, then a contravariant generic parameter of B can accept A, opposite to covariant behavior which preserves the direction of inheritance. Covariant types allow a subtype to be substituted wherever a supertype is expected, commonly used in output or return positions, while contravariant types are primarily applied in input positions or parameters. The key difference lies in their variance direction: covariance maintains the subtype relationship, contravariance inverts it, which affects how types are substituted in generic programming and type safety.
Advantages and Challenges of Each Approach
Covariant types enhance flexibility in programming by allowing a subtype relationship to be preserved, making code more reusable and easier to understand, particularly in object-oriented design. Contravariant types improve adaptability when dealing with function inputs, enabling safer and more precise control over method argument types, which is critical in event handling and callback systems. Covariance can lead to type safety concerns in mutable structures, while contravariance complicates type inference and may require more explicit type annotations, posing challenges for developers in maintaining clear and error-free code.
Summary and Future Directions
Contravariant and covariant types define how subtype relationships are preserved in type systems, with covariant types allowing substitution with subtypes and contravariant types with supertypes. Summary analyses highlight their critical roles in function types, generics, and type safety, emphasizing that covariant positions accept more specific types while contravariant positions accept more general ones. Future directions include refining type inference algorithms to better handle variance annotations, expanding practical applications in advanced type-checking for programming languages, and integrating variance concepts into machine learning type systems for enhanced model robustness.
Contravariate Infographic
 libterm.com
libterm.com