Modules serve as essential building blocks in various systems, enabling customization and scalability to meet specific needs. By selecting the appropriate module category, you can enhance efficiency and functionality tailored to your project requirements. Explore the rest of the article to discover the best module categories for your application.
Table of Comparison
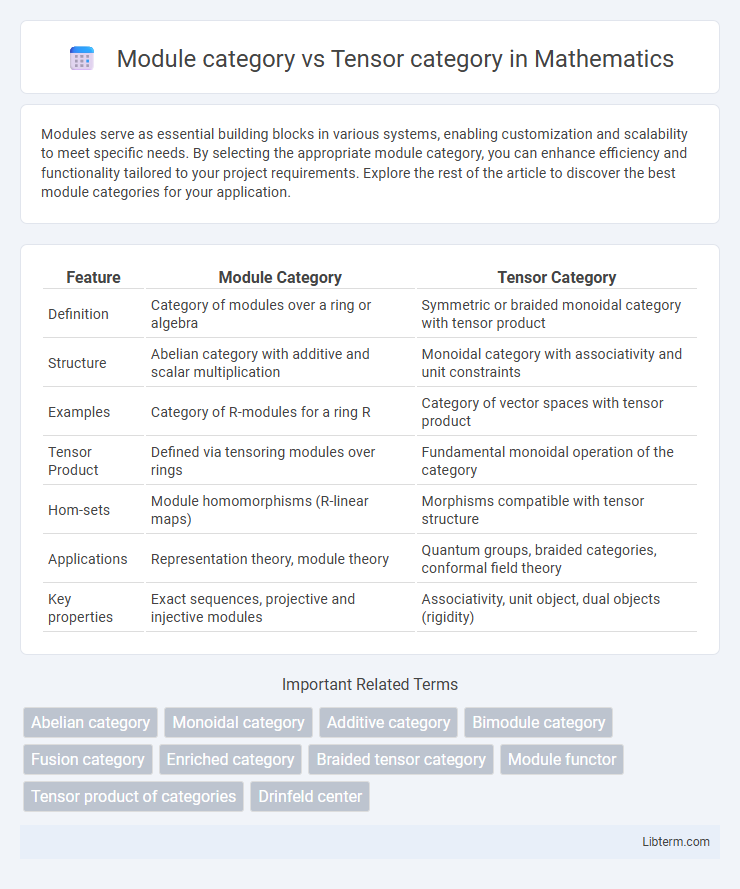
| Feature | Module Category | Tensor Category |
|---|---|---|
| Definition | Category of modules over a ring or algebra | Symmetric or braided monoidal category with tensor product |
| Structure | Abelian category with additive and scalar multiplication | Monoidal category with associativity and unit constraints |
| Examples | Category of R-modules for a ring R | Category of vector spaces with tensor product |
| Tensor Product | Defined via tensoring modules over rings | Fundamental monoidal operation of the category |
| Hom-sets | Module homomorphisms (R-linear maps) | Morphisms compatible with tensor structure |
| Applications | Representation theory, module theory | Quantum groups, braided categories, conformal field theory |
| Key properties | Exact sequences, projective and injective modules | Associativity, unit object, dual objects (rigidity) |
Introduction to Module Categories and Tensor Categories
Module categories generalize tensor categories by allowing an action of a tensor category on another category, enriching the structure with additional module-like behavior. Tensor categories are rigid, monoidal categories with duals and associativity constraints central to areas like quantum groups and representation theory. Understanding module categories involves exploring how tensor categories act on and interact with other categories, extending the framework of tensor categories beyond their intrinsic monoidal properties.
Mathematical Foundations: Modules and Tensors
Module categories extend module theory by allowing objects to carry an action over a tensor category, generalizing module structures from rings to monoidal categories. Tensor categories provide a rigid framework where objects have tensor products and duals, facilitating the study of algebraic and topological structures through categorical operations. The interplay between module categories and tensor categories enables a deeper understanding of representation theory, monoidal functors, and braided or fusion category theory.
Defining Module Categories
A module category over a tensor category is defined as an abelian category equipped with an exact bifunctor that satisfies associativity and unit constraints compatible with the tensor product structure. This bifunctor acts as a tensorial action of the tensor category on the module category, generalizing module theory to a categorical framework. The concept formalizes how objects in the tensor category "act" on objects in the module category, preserving structural coherence crucial for applications in representation theory and quantum algebra.
Defining Tensor Categories
Tensor categories are rigid monoidal categories equipped with associativity, unit constraints, and duals, serving as a framework to formalize tensor products in representation theory and quantum algebra. Module categories arise as categories acted upon by a tensor category, generalizing the notion of modules over an algebra to a categorical setting. The definition of tensor categories hinges on the coherence of tensor product functors and the existence of dual objects, distinguishing them from module categories, which lack an intrinsic monoidal structure.
Key Differences Between Module and Tensor Categories
Module categories are categories equipped with an action from a monoidal category, often used to study representations of algebras and their modules, whereas tensor categories are rigid monoidal categories with additional structures like duals and associators that enable tensor operations. Key differences include the role of modules as objects that "live over" another category versus tensor categories serving as a framework for internal tensor products and intrinsic duality. Module categories emphasize external actions and representations, while tensor categories focus on internal tensor product operations and categorical symmetries.
Structural Properties and Morphisms
Module categories over a tensor category exhibit enriched structural properties such as the presence of exact module functors and internal Hom objects, reflecting the module's action compatibility with the tensor product. Morphisms in module categories are module functors respecting the module structure, preserving the module action, while morphisms in tensor categories are tensor functors preserving the monoidal structure, tensor product, and associativity constraints. The interplay between these morphisms dictates coherence conditions and enables the study of module categories as enriched categories over tensor categories, crucial for applications in representation theory and quantum algebra.
Applications of Module Categories
Module categories extend tensor categories by incorporating actions of tensor categories on other categories, enabling richer structural frameworks. Applications of module categories include representation theory, where they model modules over algebra objects in tensor categories, and topological quantum field theory, facilitating the study of boundary conditions and defects. These structures also play a critical role in categorifying algebraic concepts and in constructing invariants in low-dimensional topology.
Applications of Tensor Categories
Tensor categories provide a rich framework for studying symmetries in quantum groups, topological quantum field theories, and conformal field theories, enabling the classification of particle-like excitations and braid group representations. Module categories extend this framework by describing actions of tensor categories on other linear categories, crucial for understanding boundary conditions, defects in topological phases, and Morita theory for tensor categories. Applications of tensor categories in quantum computing, particularly in modeling anyons and fault-tolerant quantum gates, depend heavily on the interplay with module categories to capture module actions and bimodule structures.
Interrelation and Overlaps Between the Categories
Module categories and tensor categories share a deep interrelation where module categories can be viewed as categories acted upon by a tensor category, enabling the study of representations within a unified framework. This overlap is prominent in areas like fusion categories, where module categories classify extensions and bimodule categories describe Morita equivalences between tensor categories. The interaction between these categories enriches the understanding of algebraic structures, categorical invariants, and topological quantum field theories.
Future Directions and Open Problems in Category Theory
Future research in category theory focuses on deepening the understanding of the interplay between module categories and tensor categories, particularly in areas such as fusion categories and their applications to quantum computing. Open problems include classifying module categories over non-semisimple tensor categories and exploring the extension of tensor categorical frameworks to infinite dimensions and higher categories. Advances in these directions will enhance the mathematical foundations of topological quantum field theories and categorical representation theory.
Module category Infographic
 libterm.com
libterm.com