Quadratic mean, also called root mean square (RMS), is a statistical measure used to determine the average magnitude of a set of numbers, especially when values can be both positive and negative. It is calculated by squaring each value, finding their mean, and then taking the square root of that mean, a method particularly useful in fields like engineering and physics for analyzing waveform amplitudes and signal strengths. Discover how understanding the quadratic mean can enhance Your data analysis and interpretation by reading the full article.
Table of Comparison
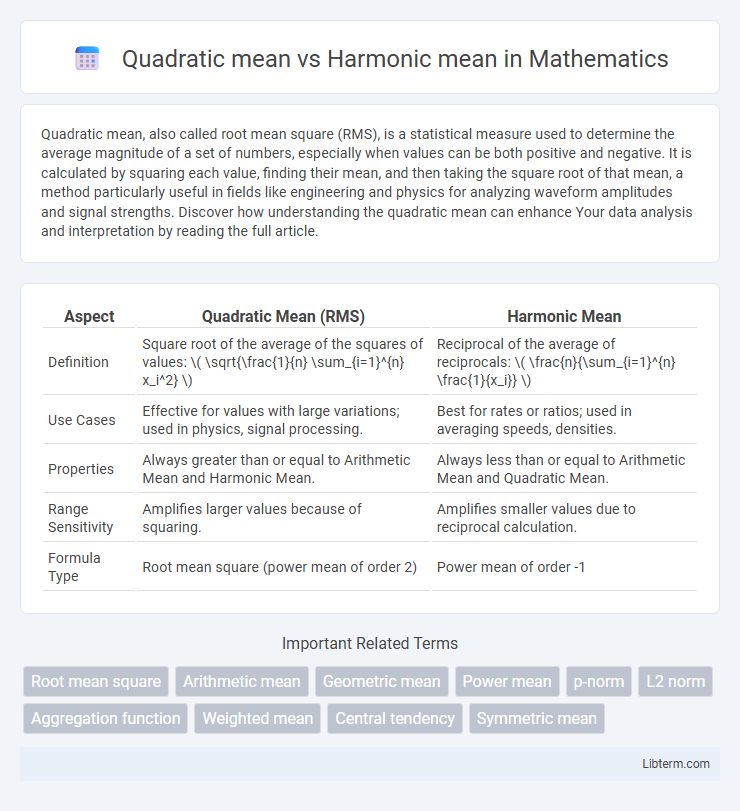
| Aspect | Quadratic Mean (RMS) | Harmonic Mean |
|---|---|---|
| Definition | Square root of the average of the squares of values: \( \sqrt{\frac{1}{n} \sum_{i=1}^{n} x_i^2} \) | Reciprocal of the average of reciprocals: \( \frac{n}{\sum_{i=1}^{n} \frac{1}{x_i}} \) |
| Use Cases | Effective for values with large variations; used in physics, signal processing. | Best for rates or ratios; used in averaging speeds, densities. |
| Properties | Always greater than or equal to Arithmetic Mean and Harmonic Mean. | Always less than or equal to Arithmetic Mean and Quadratic Mean. |
| Range Sensitivity | Amplifies larger values because of squaring. | Amplifies smaller values due to reciprocal calculation. |
| Formula Type | Root mean square (power mean of order 2) | Power mean of order -1 |
Introduction to Means: An Overview
The quadratic mean, also known as the root mean square, measures the average magnitude of a set of numbers by squaring values, calculating their mean, and taking the square root, making it sensitive to larger values. The harmonic mean calculates the average rate when dealing with ratios or rates by taking the reciprocal of the arithmetic mean of reciprocals, emphasizing smaller values more heavily. Both means serve distinct functions in statistical analysis, with the quadratic mean suitable for datasets with varying magnitudes and the harmonic mean ideal for rate-based or ratio-based data.
Defining the Quadratic Mean
The quadratic mean, also known as the root mean square (RMS), is calculated by taking the square root of the average of the squares of a set of values, making it particularly effective for measuring varying magnitudes. It emphasizes larger values more than the arithmetic mean or harmonic mean, commonly used in statistics, physics, and electrical engineering to assess the magnitude of varying quantities. The harmonic mean, by contrast, is the reciprocal of the average of reciprocals and is more sensitive to smaller values, often applied in rates and ratios analysis.
Understanding the Harmonic Mean
The harmonic mean is calculated as the reciprocal of the average of reciprocals, making it especially useful for averaging ratios or rates, such as speed or density. Unlike the quadratic mean, which emphasizes larger values by squaring, the harmonic mean gives greater weight to smaller values, providing a more accurate measure when lower numbers dominate the dataset. This property makes the harmonic mean ideal for scenarios involving rates or ratios, ensuring balanced representation where extreme large values might otherwise distort the average.
Mathematical Formulas: Quadratic vs Harmonic Mean
The quadratic mean, or root mean square, is calculated using the formula \( \sqrt{\frac{1}{n} \sum_{i=1}^n x_i^2} \), emphasizing the square of the values before averaging. The harmonic mean is determined by \( \frac{n}{\sum_{i=1}^n \frac{1}{x_i}} \), focusing on the reciprocal of the values for averaging. Both means serve different purposes, with the quadratic mean typically used for magnitude analysis and the harmonic mean for rates or ratios.
Key Differences Between Quadratic and Harmonic Means
The quadratic mean, also known as the root mean square, calculates the square root of the average of the squares of a set of numbers, emphasizing larger values and often used in contexts like signal processing. The harmonic mean, defined as the reciprocal of the average of reciprocals, is more influenced by smaller values and is beneficial for rates and ratios, such as average speeds. Key differences include sensitivity to data distribution--quadratic mean overweighting larger numbers while harmonic mean underweighting them--making each suitable for different applications depending on data characteristics.
Applications of Quadratic Mean in Real Life
The quadratic mean, also known as the root mean square, is widely used in fields such as electrical engineering to calculate effective voltage or current, reflecting energy values more accurately than arithmetic or harmonic means. In statistics and physics, it measures magnitudes of varying quantities like speeds or intensities, providing a meaningful average especially when values include both positive and negative numbers. Unlike the harmonic mean, which is ideal for rates or ratios, the quadratic mean excels in contexts involving squared quantities or where larger values have a disproportionately greater impact.
Practical Uses of Harmonic Mean
The harmonic mean is particularly useful in averaging rates, such as speeds or densities, where the total quantity is fixed but the variable changes. Unlike the quadratic mean, which emphasizes larger values, the harmonic mean gives more weight to smaller numbers, making it ideal for scenarios like calculating average travel times or financial ratios like the price-to-earnings ratio. Its practical applications extend to fields such as physics, finance, and engineering where reciprocal relationships prevail.
Quadratic Mean vs Harmonic Mean: When to Use Which?
Quadratic mean, or root mean square, emphasizes larger values making it ideal for measuring quantities like voltage or speed where magnitude variation matters, while harmonic mean is better suited for rates or ratios, such as average speed or price per unit, where smaller values carry more influence. Use quadratic mean when dealing with data containing squares or when larger errors penalize more heavily, and choose harmonic mean when averaging ratios or rates to avoid distortion by large outliers. Understanding the data distribution and context ensures selecting the appropriate mean for accurate and meaningful results.
Comparative Examples and Calculations
The quadratic mean, also known as the root mean square, calculates the square root of the average of squared values, making it particularly useful in physics for measuring varying quantities like voltage or speed, for example, RMS speed of particles in a gas is higher than arithmetic mean speed. The harmonic mean emphasizes smaller values and is ideal for rates and ratios, such as calculating average speeds over equal distances, where the overall speed is lower than the arithmetic mean due to time weighting. Comparing calculations: for values 3 and 6, the quadratic mean is ((32 + 62)/2) 4.74, whereas the harmonic mean is 2 / (1/3 + 1/6) = 4, highlighting how RMS skews higher due to squaring.
Conclusion: Choosing the Right Mean
Choosing between quadratic mean and harmonic mean depends on the nature of the data and the desired emphasis. Quadratic mean, also known as root mean square, is optimal for datasets where larger values have a stronger impact, such as in physics or engineering contexts involving power or signal strength. Harmonic mean is preferable for rates or ratios, especially when averaging speeds or densities, as it better accounts for the influence of smaller values.
Quadratic mean Infographic
 libterm.com
libterm.com