Temperley-Lieb algebra plays a crucial role in statistical mechanics and quantum computing by providing a framework for understanding link invariants and planar diagrams. Its applications extend to solving problems in knot theory and designing algorithms for topological quantum computers. Explore the rest of this article to uncover how your research or projects can leverage the powerful structures within the Temperley-Lieb algebra.
Table of Comparison
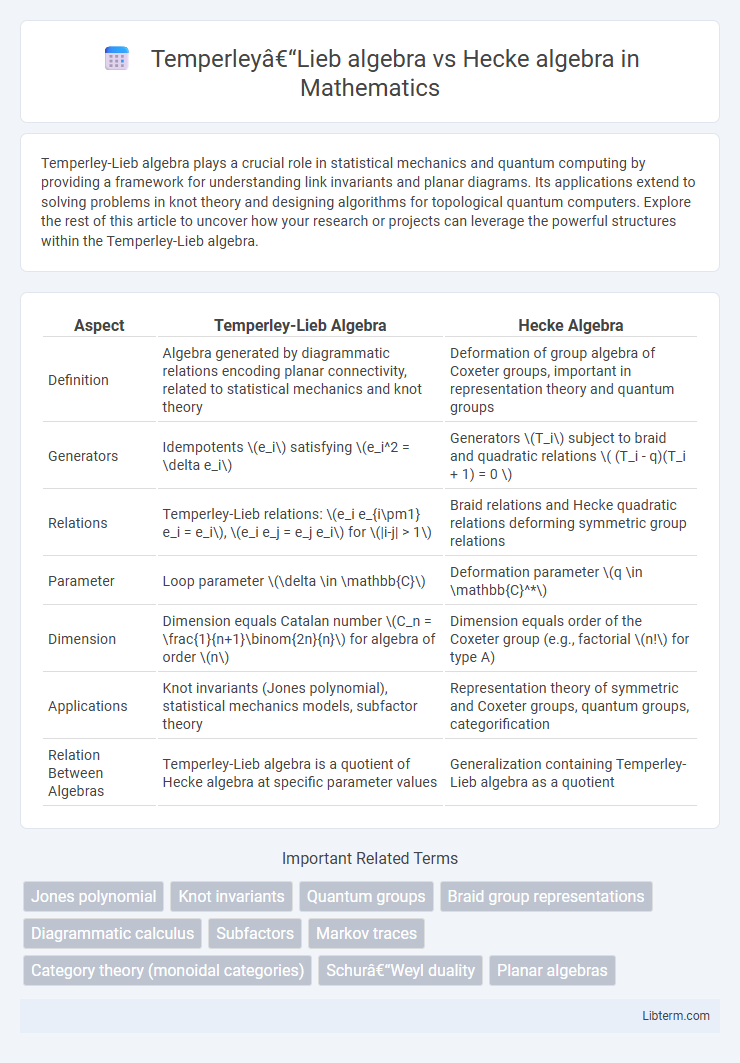
| Aspect | Temperley-Lieb Algebra | Hecke Algebra |
|---|---|---|
| Definition | Algebra generated by diagrammatic relations encoding planar connectivity, related to statistical mechanics and knot theory | Deformation of group algebra of Coxeter groups, important in representation theory and quantum groups |
| Generators | Idempotents \(e_i\) satisfying \(e_i^2 = \delta e_i\) | Generators \(T_i\) subject to braid and quadratic relations \( (T_i - q)(T_i + 1) = 0 \) |
| Relations | Temperley-Lieb relations: \(e_i e_{i\pm1} e_i = e_i\), \(e_i e_j = e_j e_i\) for \(|i-j| > 1\) | Braid relations and Hecke quadratic relations deforming symmetric group relations |
| Parameter | Loop parameter \(\delta \in \mathbb{C}\) | Deformation parameter \(q \in \mathbb{C}^*\) |
| Dimension | Dimension equals Catalan number \(C_n = \frac{1}{n+1}\binom{2n}{n}\) for algebra of order \(n\) | Dimension equals order of the Coxeter group (e.g., factorial \(n!\) for type A) |
| Applications | Knot invariants (Jones polynomial), statistical mechanics models, subfactor theory | Representation theory of symmetric and Coxeter groups, quantum groups, categorification |
| Relation Between Algebras | Temperley-Lieb algebra is a quotient of Hecke algebra at specific parameter values | Generalization containing Temperley-Lieb algebra as a quotient |
Introduction to Temperley–Lieb and Hecke Algebras
Temperley-Lieb algebra and Hecke algebra are significant structures in algebraic combinatorics and quantum group theory, with Temperley-Lieb algebra originating from statistical mechanics and knot theory, characterized by generators subject to specific relations that simplify diagrammatic calculations. Hecke algebra generalizes the group algebra of Coxeter groups, parameterized by a deformation variable q, playing a crucial role in representation theory and categorification. Both algebras facilitate the understanding of braiding and knot invariants, but Temperley-Lieb algebra specializes in planar diagrams while Hecke algebra provides a broader framework linked to quantum groups and symmetric functions.
Historical Background and Development
The Temperley-Lieb algebra originated in the 1970s from statistical mechanics and knot theory, introduced by Temperley and Lieb to study models like the Potts model and ice-type models. The Hecke algebra, developed earlier in the mid-20th century through works by Erich Hecke, emerged from the representation theory of Coxeter groups and symmetric groups. Both algebras have since influenced the development of quantum groups and low-dimensional topology, with the Temperley-Lieb algebra serving as a quotient of the Hecke algebra associated with type A Coxeter groups.
Algebraic Structures and Definitions
Temperley-Lieb algebra is an associative algebra defined via generators and relations linked to planar diagrams representing non-crossing pairings, often used in statistical mechanics and knot theory. Hecke algebra generalizes the group algebra of Coxeter groups with deformation parameters, playing a crucial role in representation theory and categorification. Both algebras exhibit rich structures with Temperley-Lieb as a quotient of Hecke algebra at specific parameter values, connecting diagrammatic and algebraic perspectives.
Key Generators and Relations
The Temperley-Lieb algebra is generated by elements \( e_i \) subject to relations \( e_i^2 = \delta e_i \), \( e_i e_{i \pm 1} e_i = e_i \), and \( e_i e_j = e_j e_i \) for \(|i - j| > 1\), where \(\delta\) is a parameter related to the loop value. The Hecke algebra is generated by elements \( T_i \) satisfying the braid relations \( T_i T_{i+1} T_i = T_{i+1} T_i T_{i+1} \) and quadratic relations \( (T_i - q)(T_i + 1) = 0 \), where \( q \) is a deformation parameter. Both algebras arise in representation theory and statistical mechanics, with the Temperley-Lieb algebra serving as a quotient of the Hecke algebra under specific conditions on \( q \) and \(\delta\).
Representation Theory: Similarities and Differences
Temperley-Lieb algebra and Hecke algebra both play significant roles in representation theory, particularly through their connections to braid groups and quantum groups. Temperley-Lieb algebra emerges as a quotient of the Hecke algebra of type A, characterized by idempotent generators and diagrammatic interpretations linked to statistical mechanics and knot theory. Representation theory of Temperley-Lieb algebra is simpler with cell modules indexed by link patterns, while Hecke algebra representations are richer, linked to symmetric group representations and Kazhdan-Lusztig theory.
Diagrammatic Interpretations
Temperley-Lieb algebra features diagrammatic interpretations based on planar diagrams of non-crossing pairings, which correspond to certain link patterns and play a critical role in statistical mechanics models. Hecke algebra diagrams utilize braid group generators that encode crossings and are essential in knot theory and representation theory of quantum groups. The diagrammatic differences highlight that Temperley-Lieb algebras emphasize planar connectivity while Hecke algebras capture braid-like structures with crossing information.
Connections with Knot Theory and Statistical Mechanics
The Temperley-Lieb algebra and Hecke algebra both play crucial roles in knot theory through their connections to link invariants, with the Temperley-Lieb algebra underpinning the Jones polynomial and the Hecke algebra relating to the HOMFLY-PT polynomial. In statistical mechanics, the Temperley-Lieb algebra models the transfer matrix in the Potts and ice-type models, establishing a bridge between algebraic structures and phase transitions. Meanwhile, the Hecke algebra arises in exactly solvable lattice models and quantum groups, facilitating the analysis of integrable systems and symmetry properties.
Role in Quantum Groups and Categorification
Temperley-Lieb algebra serves as a diagrammatic tool in the representation theory of quantum groups, particularly linked to the quantum group \( U_q(\mathfrak{sl}_2) \), providing a categorification framework for knot invariants and low-dimensional topology. Hecke algebra generalizes symmetric group algebras and plays a fundamental role in the categorification of quantum groups associated with higher rank Lie algebras, enabling categorified braid group actions and connections to canonical bases. Both algebras facilitate categorification by encoding algebraic and topological structures within monoidal categories, advancing the understanding of quantum symmetries and invariants.
Applications in Mathematical Physics
Temperley-Lieb algebra plays a crucial role in the study of exactly solvable models in statistical mechanics, particularly in the analysis of the Potts model and ice-type models, where it encodes the connectivity properties of loop models. Hecke algebra finds significant applications in quantum groups and knot theory, facilitating the construction of invariants such as the Jones polynomial and providing algebraic frameworks for integrable systems and representation theory. Both algebras contribute fundamentally to the understanding of topological quantum field theories (TQFTs) and are instrumental in exploring symmetries and fusion categories in mathematical physics.
Comparative Summary and Future Directions
Temperley-Lieb algebra and Hecke algebra serve distinct roles in representation theory and statistical mechanics, with the former emerging from the study of planar algebras and link invariants, while the latter generalizes symmetric groups through q-deformations. Temperley-Lieb algebra emphasizes diagrammatic calculus and connections to knot theory, offering computational advantages in low-dimensional topology, whereas Hecke algebra provides a richer algebraic structure pivotal in quantum groups and categorifications. Future research aims to unify these frameworks via categorification and explore their applications in quantum computing, topological phases, and advanced knot homologies.
Temperley–Lieb algebra Infographic
 libterm.com
libterm.com