Harmonic mean is a type of average best used for rates and ratios, calculated by dividing the number of values by the sum of their reciprocals. It provides a more accurate measure when dealing with quantities like speed or density, where the average of rates is needed rather than the average of absolute values. Discover how understanding harmonic mean can enhance your data analysis by exploring the rest of this article.
Table of Comparison
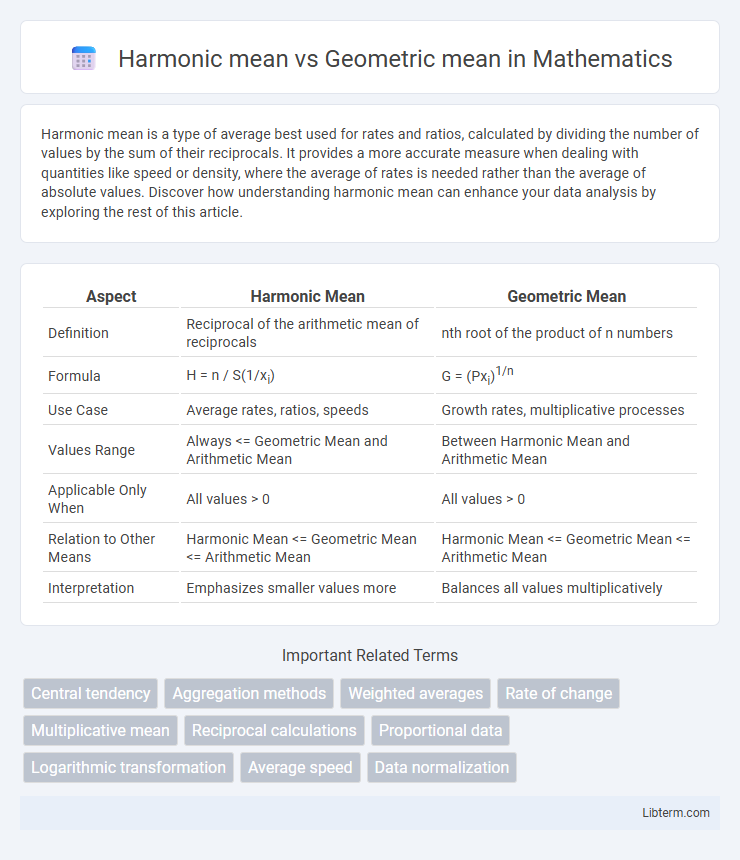
| Aspect | Harmonic Mean | Geometric Mean |
|---|---|---|
| Definition | Reciprocal of the arithmetic mean of reciprocals | nth root of the product of n numbers |
| Formula | H = n / S(1/xi) | G = (Pxi)1/n |
| Use Case | Average rates, ratios, speeds | Growth rates, multiplicative processes |
| Values Range | Always <= Geometric Mean and Arithmetic Mean | Between Harmonic Mean and Arithmetic Mean |
| Applicable Only When | All values > 0 | All values > 0 |
| Relation to Other Means | Harmonic Mean <= Geometric Mean <= Arithmetic Mean | Harmonic Mean <= Geometric Mean <= Arithmetic Mean |
| Interpretation | Emphasizes smaller values more | Balances all values multiplicatively |
Introduction to Harmonic Mean and Geometric Mean
The harmonic mean is defined as the reciprocal of the arithmetic mean of reciprocals, commonly used to average rates or ratios such as speed or density. The geometric mean calculates the nth root of the product of n values and is especially effective for growth rates and multiplicative processes. Both means provide different perspectives on datasets, with the harmonic mean emphasizing smaller values and the geometric mean capturing central tendency in exponential data.
Definitions and Formulas
The harmonic mean is the reciprocal of the arithmetic mean of reciprocals, calculated as n divided by the sum of the reciprocals of the data points, useful for rates and ratios. The geometric mean is the nth root of the product of n positive numbers, representing the central tendency of multiplicative data. Both means provide different insights: the harmonic mean emphasizes smaller values, while the geometric mean balances proportional growth across data sets.
Key Differences between Harmonic and Geometric Mean
The harmonic mean is calculated as the reciprocal of the average of reciprocals, emphasizing smaller values and minimizing the impact of larger outliers, commonly used in rates and ratios. The geometric mean multiplies all values and then takes the nth root, providing a balanced average suitable for data with exponential growth or proportional changes. Key differences include harmonic mean's sensitivity to low values and appropriateness for averaging rates, whereas geometric mean is ideal for multiplicative datasets and growth rates.
Calculation Methods with Examples
The harmonic mean is calculated by dividing the number of values by the sum of the reciprocals of the values, commonly used for rates such as speed or density; for example, the harmonic mean of 2, 4, and 6 is 3 / (1/2 + 1/4 + 1/6) 3. The geometric mean is obtained by multiplying all the values together and then taking the nth root (where n is the number of values), ideal for growth rates or percentages; for instance, the geometric mean of 2, 4, and 8 is (2 x 4 x 8)^(1/3) = 4. Each mean emphasizes different aspects of the dataset, with the harmonic mean reducing the impact of large outliers and the geometric mean reflecting proportional growth.
Applications of Harmonic Mean
The harmonic mean is widely used in fields such as finance for averaging ratios like price-to-earnings ratios, and in physics to calculate average speeds when distances are constant. It is also critical in engineering for systems with rates, such as electrical resistances in parallel circuits. These applications leverage the harmonic mean's ability to accurately represent average rates and ratios, especially when values are inversely related.
Applications of Geometric Mean
Geometric mean is widely used in finance to calculate compound interest rates and investment returns, providing a more accurate measure of average growth over time compared to arithmetic mean. It is essential in fields like biology and environmental science for averaging ratios, rates of change, and population growth, where data are multiplicative. Unlike harmonic mean, which is preferable for averaging rates like speed, geometric mean effectively handles proportional growth and exponential measures across diverse applications.
Advantages and Limitations of Harmonic Mean
The harmonic mean excels in averaging rates and ratios, making it ideal for scenarios like calculating average speed or price-to-earnings ratios, where values are inversely related. Its advantage lies in giving less weight to large outliers, providing a more accurate representation when small values dominate the dataset. However, the harmonic mean is limited by its sensitivity to zero or negative values, as it cannot handle non-positive numbers, which restricts its applicability in datasets containing such values.
Advantages and Limitations of Geometric Mean
Geometric mean excels in analyzing proportional growth rates and datasets with varying ranges, making it ideal for financial returns and ratio-based data. Its advantage lies in mitigating the impact of extreme values by emphasizing multiplicative relationships rather than additive differences. However, the geometric mean is limited by its inability to handle negative or zero values, restricting its applicability to strictly positive datasets and complicating analysis when data includes non-positive numbers.
Choosing the Appropriate Mean in Data Analysis
Choosing between harmonic mean and geometric mean depends on the nature of data and analysis goals. Harmonic mean is optimal for average rates or ratios, particularly when dealing with speed, efficiency, or cost per unit, minimizing the impact of large outliers. Geometric mean is suitable for multiplicative or proportional growth data, such as investment returns or population studies, providing a more accurate central tendency when values vary exponentially.
Summary and Conclusion
Harmonic mean excels in averaging rates or ratios, especially when values represent parts of a whole, minimizing the impact of large outliers. Geometric mean provides a better measure for growth rates and proportional changes by emphasizing multiplicative relationships and smoothing skewed data. Choosing between harmonic and geometric means depends on data context: harmonic mean suits rate-focused scenarios, while geometric mean fits growth and compounding analyses.
Harmonic mean Infographic
 libterm.com
libterm.com