Entropy measures the degree of disorder or randomness in a system, playing a crucial role in thermodynamics and information theory. Understanding entropy helps you grasp how energy disperses and how uncertainty increases in natural processes. Explore the rest of this article to discover the fascinating implications of entropy in science and technology.
Table of Comparison
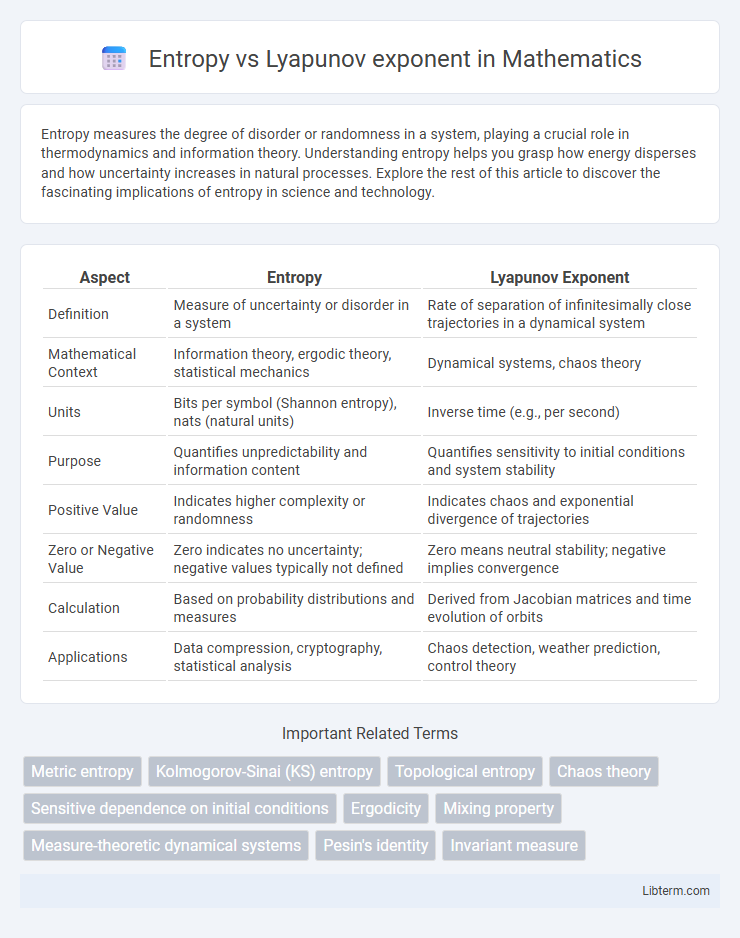
| Aspect | Entropy | Lyapunov Exponent |
|---|---|---|
| Definition | Measure of uncertainty or disorder in a system | Rate of separation of infinitesimally close trajectories in a dynamical system |
| Mathematical Context | Information theory, ergodic theory, statistical mechanics | Dynamical systems, chaos theory |
| Units | Bits per symbol (Shannon entropy), nats (natural units) | Inverse time (e.g., per second) |
| Purpose | Quantifies unpredictability and information content | Quantifies sensitivity to initial conditions and system stability |
| Positive Value | Indicates higher complexity or randomness | Indicates chaos and exponential divergence of trajectories |
| Zero or Negative Value | Zero indicates no uncertainty; negative values typically not defined | Zero means neutral stability; negative implies convergence |
| Calculation | Based on probability distributions and measures | Derived from Jacobian matrices and time evolution of orbits |
| Applications | Data compression, cryptography, statistical analysis | Chaos detection, weather prediction, control theory |
Introduction to Entropy and Lyapunov Exponent
Entropy measures the unpredictability and information content in a dynamic system, quantifying the rate of information production over time. The Lyapunov exponent evaluates the sensitivity to initial conditions by measuring the exponential rate of divergence or convergence of nearby trajectories in phase space. Both concepts provide critical insights into chaos theory, with entropy focusing on system complexity and randomness, while the Lyapunov exponent emphasizes stability and predictability.
Defining Entropy in Dynamical Systems
Entropy in dynamical systems quantifies the rate of information production and measures the system's unpredictability, typically defined using measure-theoretic entropy or Kolmogorov-Sinai entropy. It captures the average exponential growth rate of distinguishable orbits over time, reflecting the system's complexity and chaotic behavior. Unlike the Lyapunov exponent, which measures the average exponential divergence of nearby trajectories, entropy provides a global statistical description of dynamical unpredictability.
Understanding Lyapunov Exponents
Lyapunov exponents quantify the rate at which nearby trajectories in a dynamical system diverge, providing a measure of chaos by indicating sensitivity to initial conditions. Unlike entropy, which assesses the overall unpredictability or information production of a system, Lyapunov exponents focus specifically on exponential divergence in phase space. Calculating the largest Lyapunov exponent is crucial for distinguishing chaotic behavior from regular dynamics in complex systems analysis.
Mathematical Formulation of Entropy
Entropy in dynamical systems is mathematically formulated using measure-theoretic entropy, defined as the supremum of the Shannon entropies over all finite measurable partitions of the phase space. For a measurable map \( T \) on a probability space \((X, \mathcal{B}, \mu)\), the entropy \( h_\mu(T) \) quantifies the average information produced per iteration and is given by \( h_\mu(T) = \sup_{\mathcal{P}} \lim_{n \to \infty} \frac{1}{n} H\left(\bigvee_{i=0}^{n-1} T^{-i} \mathcal{P}\right) \), where \( H(\mathcal{P}) \) denotes the Shannon entropy of the partition \( \mathcal{P} \). This contrasts with the Lyapunov exponent measuring exponential divergence of trajectories, as entropy provides a global statistical complexity rather than a local stability metric.
Calculating Lyapunov Exponents: A Step-by-Step Guide
Calculating Lyapunov exponents involves first identifying a dynamical system's trajectory and then tracking the divergence of nearby trajectories over time, which quantifies the system's sensitivity to initial conditions. The process begins by numerically integrating the system's equations to generate a reference orbit, followed by evolving a tangent vector that encodes infinitesimal perturbations using the system's Jacobian matrix. The Lyapunov exponent is obtained by averaging the logarithm of the growth rate of these perturbations, typically through repeated renormalizations to ensure numerical stability and convergence.
Entropy vs Lyapunov Exponent: Key Differences
Entropy measures the average rate of information production or uncertainty in a dynamical system, reflecting its complexity and unpredictability. The Lyapunov exponent quantifies the average exponential rate of divergence or convergence of nearby trajectories, indicating the system's sensitivity to initial conditions. Key differences include entropy representing statistical randomness and information content, while the Lyapunov exponent describes local stability and chaos through trajectory separation rates.
Physical Interpretations and Applications
Entropy quantifies the uncertainty and disorder within a dynamical system, reflecting the rate at which information about the system's state is lost over time. The Lyapunov exponent measures the exponential rate of divergence between nearby trajectories, directly indicating the system's sensitivity to initial conditions and chaotic behavior. In physical applications, entropy is used to assess thermodynamic irreversibility and information flow, while the Lyapunov exponent aids in predicting predictability limits in weather forecasting, fluid dynamics, and mechanical systems.
Relationship between Entropy and Chaos
Entropy quantifies the rate of information production in a dynamical system, serving as a measure of unpredictability and complexity. The Lyapunov exponent measures the average exponential divergence of nearby trajectories, indicating the sensitivity to initial conditions characteristic of chaotic systems. A positive Lyapunov exponent corresponds to positive entropy, establishing a direct relationship between chaos and the system's intrinsic unpredictability.
Lyapunov Exponent in Predicting Chaos
Lyapunov exponent quantifies the average rate at which nearby trajectories in a dynamical system diverge, serving as a precise measure to predict chaos by indicating sensitivity to initial conditions. Positive Lyapunov exponents signal exponential divergence of trajectories, confirming the presence of chaotic behavior and enabling early detection of system instability. Unlike entropy, which measures system disorder or unpredictability, the Lyapunov exponent directly characterizes the dynamical instability crucial for chaos prediction in complex systems.
Comparative Analysis: Choosing the Right Measure
Entropy and Lyapunov exponents both quantify aspects of dynamical system complexity, with entropy measuring the rate of information production and unpredictability, while Lyapunov exponents assess the average exponential divergence of nearby trajectories indicating chaos sensitivity. Entropy is often preferred for characterizing overall system disorder and information content, especially in symbolic dynamics and information theory contexts, whereas Lyapunov exponents provide direct insight into stability and chaos by quantifying local divergence rates in phase space. Selecting the appropriate measure depends on the analysis goal: use entropy for global system unpredictability and information generation, and Lyapunov exponents for precise evaluation of chaotic behavior and trajectory sensitivity.
Entropy Infographic
 libterm.com
libterm.com