Centralization consolidates decision-making authority at the top levels of management, enhancing consistency and control across an organization. This approach streamlines processes and ensures uniformity, which can boost efficiency and reduce redundancy. Explore the rest of the article to understand how centralization impacts your organization's structure and performance.
Table of Comparison
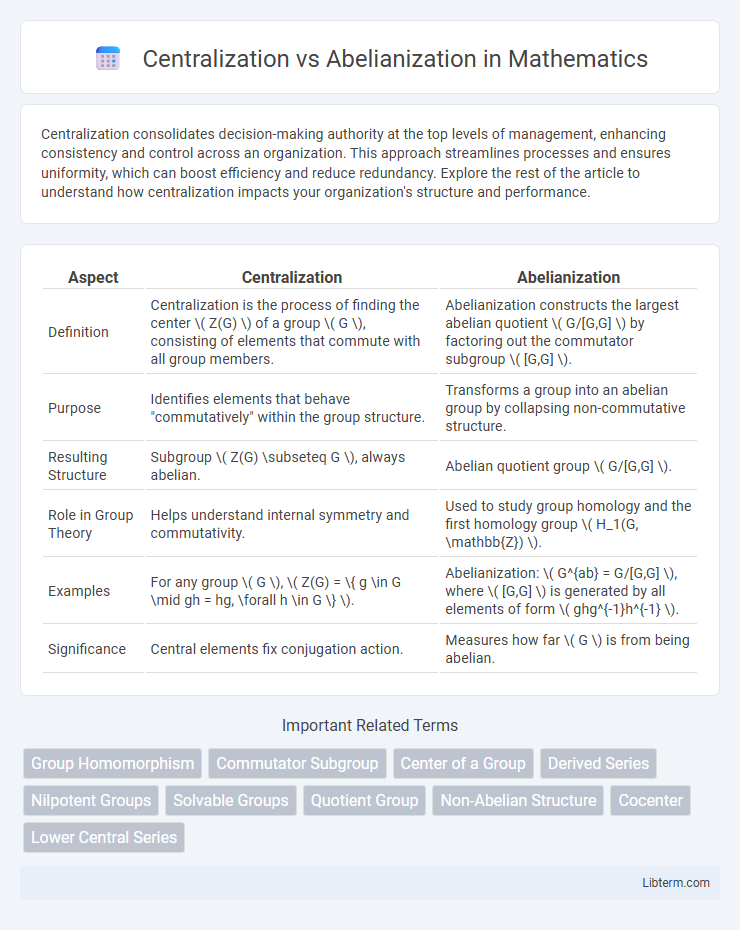
| Aspect | Centralization | Abelianization |
|---|---|---|
| Definition | Centralization is the process of finding the center \( Z(G) \) of a group \( G \), consisting of elements that commute with all group members. | Abelianization constructs the largest abelian quotient \( G/[G,G] \) by factoring out the commutator subgroup \( [G,G] \). |
| Purpose | Identifies elements that behave "commutatively" within the group structure. | Transforms a group into an abelian group by collapsing non-commutative structure. |
| Resulting Structure | Subgroup \( Z(G) \subseteq G \), always abelian. | Abelian quotient group \( G/[G,G] \). |
| Role in Group Theory | Helps understand internal symmetry and commutativity. | Used to study group homology and the first homology group \( H_1(G, \mathbb{Z}) \). |
| Examples | For any group \( G \), \( Z(G) = \{ g \in G \mid gh = hg, \forall h \in G \} \). | Abelianization: \( G^{ab} = G/[G,G] \), where \( [G,G] \) is generated by all elements of form \( ghg^{-1}h^{-1} \). |
| Significance | Central elements fix conjugation action. | Measures how far \( G \) is from being abelian. |
Introduction to Centralization and Abelianization
Centralization in algebra refers to the process of identifying the center of a group, consisting of elements that commute with all other group members and thus reveal intrinsic symmetries. Abelianization transforms a group into its abelian counterpart by factoring out the commutator subgroup, effectively "flattening" the group structure to ensure commutativity. Both concepts highlight pivotal ways to simplify and analyze group structures through commutation properties, essential in advanced algebraic studies.
Defining Centralization in Group Theory
Centralization in group theory refers to the centralizer of a subset within a group, defined as the set of elements that commute with every element of that subset, forming a subgroup known as the centralizer. This concept is crucial for understanding the structure of groups by identifying elements that maintain commutation relations, helping to analyze group symmetry and normal subgroups. Centralization contrasts with abelianization, which constructs the largest abelian quotient of a group by factoring out the commutator subgroup, transforming non-abelian groups into abelian ones.
Understanding Abelianization: Concept and Purpose
Abelianization transforms a given group into its largest abelian quotient by factoring out the commutator subgroup, enabling the study of group properties through simpler, commutative structures. This process reveals insights about the original group's structure by capturing its "abelian essence," which is crucial in fields like algebraic topology and group theory. Understanding abelianization aids in analyzing homomorphisms and simplifies complex problems by focusing on commutative behavior within non-abelian groups.
Key Differences Between Centralization and Abelianization
Centralization in algebraic structures refers to the process of forming the center of a group, consisting of elements that commute with all other elements, whereas Abelianization transforms a group into its largest abelian quotient by factoring out the commutator subgroup. The key difference lies in centralization preserving the subgroup within the original group's structure, while abelianization produces a new group where all elements commute. Centralization emphasizes internal symmetry captured by the center, whereas abelianization enforces total commutativity by collapsing non-commuting elements.
Algebraic Structures and Their Centralizers
Centralization in algebraic structures involves studying elements that commute with a given subset, forming centralizers that reveal symmetry and invariant properties within groups or rings. Abelianization transforms non-abelian groups into abelian ones by quotienting out the commutator subgroup, simplifying the structure to focus on commutative aspects. Understanding centralizers aids in analyzing non-abelian behavior before abelianization, highlighting how central elements influence the progression from complex to simplified algebraic forms.
The Role of Abelianization in Simplifying Groups
Abelianization transforms a group into its largest abelian quotient by factoring out the commutator subgroup, effectively simplifying the group's structure. This process plays a crucial role in understanding complex groups by reducing them to commutative forms, which are easier to analyze and classify. By converting non-abelian groups into abelian ones, abelianization provides a fundamental tool in algebraic topology, group theory, and homological algebra.
Mathematical Applications of Centralization
Centralization in mathematics refers to the process of identifying elements that commute with a given subset, often applied in group theory to analyze the structure of groups through centralizers, which help classify conjugacy classes and normal subgroups. Abelianization transforms a group into its largest abelian quotient by factoring out its commutator subgroup, simplifying complex group structures for applications in homology and topology. Centralization aids in understanding symmetry properties and invariant elements, crucial for solving algebraic equations and studying representation theory.
Practical Implications of Abelianization
Abelianization simplifies group structures by converting non-commutative groups into abelian groups, enabling easier computations in algebraic topology and group theory. Practical applications include simplifying homology groups' calculations and enhancing the analysis of covering spaces in geometric group theory. This transformation aids in solving problems where commutativity allows leveraging linear algebra techniques for more efficient results.
Centralization vs Abelianization: Case Studies
Case studies on centralization vs abelianization highlight distinct structural transformations in algebraic systems, where centralization enforces elements within the center of a group to commute universally, while abelianization transforms a group into its largest abelian quotient by factoring out the commutator subgroup. Analysis of finite groups reveals centralization preserves subgroup hierarchy, enhancing symmetry constraints, whereas abelianization simplifies group complexity, impacting homological properties and cohomology calculations. Empirical examples from topology and algebraic geometry demonstrate that centralization maintains crucial non-abelian features, whereas abelianization facilitates linearization, aiding classification and computational efficiency.
Summary: Choosing Between Centralization and Abelianization
Centralization consolidates authority within a single entity to streamline decision-making and enforce uniform policies, enhancing efficiency but potentially limiting flexibility. Abelianization restructures groups into abelian, or commutative, frameworks to simplify complex algebraic systems, promoting greater mathematical clarity and ease of analysis. Selecting between centralization and abelianization depends on whether the priority lies in administrative control or in achieving simplified, commutative structures in algebraic contexts.
Centralization Infographic
 libterm.com
libterm.com